【笔试】20春招快手数据类笔试,Python中心极限定理,绘制ROC曲线和AUC值。
题目来源1:中国科学技术大学的牛友fancyjiang
https://www.nowcoder.com/discuss/406334?type=all&order=time&pos=&page=1
题目来源2:烟台大学的牛友,@连续。
文章参考:请看原文。哈哈,博主比较急,就没有去参考英文原文,全是从中文博客上学来的。
本文是给狮子大开口要了我150元咨询费的连续同学写的。
笔试题目
一、 3道SQL
表A,表B;两张表相同字段:id,timestamp(时间);问:B表中第一个事件之前A事件发生的数量;B表中第一个和第二个事件发生时间之内,A表A表中事件的数量;B表中第二个和第三个事件发生时间之内,A表中事件发生的数量;B表中第n个和第n+1个事件发生时间之内,A表中事件发生的数量;B表中100000个事件发生之后A表事件的数量
也是时间的表,字段:timestamp,问最后一个事件和倒数第二个事件发生的间隔时间
表A:观看直播的表,字段:userid(唯一),photoid(唯一),timestamp;表B:观看视频的表,字段:字段:userid(唯一),photoid(唯一),timestamp;求只看直播的人数占比,只看视频人数占比,两者都看人数占比
二、 2道数据科学题目,可以选择运用python或者r
(1)写出绘制ROC曲线和计算AUC值的代码
(2)证明中心极限定理
[这个证明到底是抛色子验证,还是用Python写数学公式验证啊,懵了]
Python证明中心极限定理
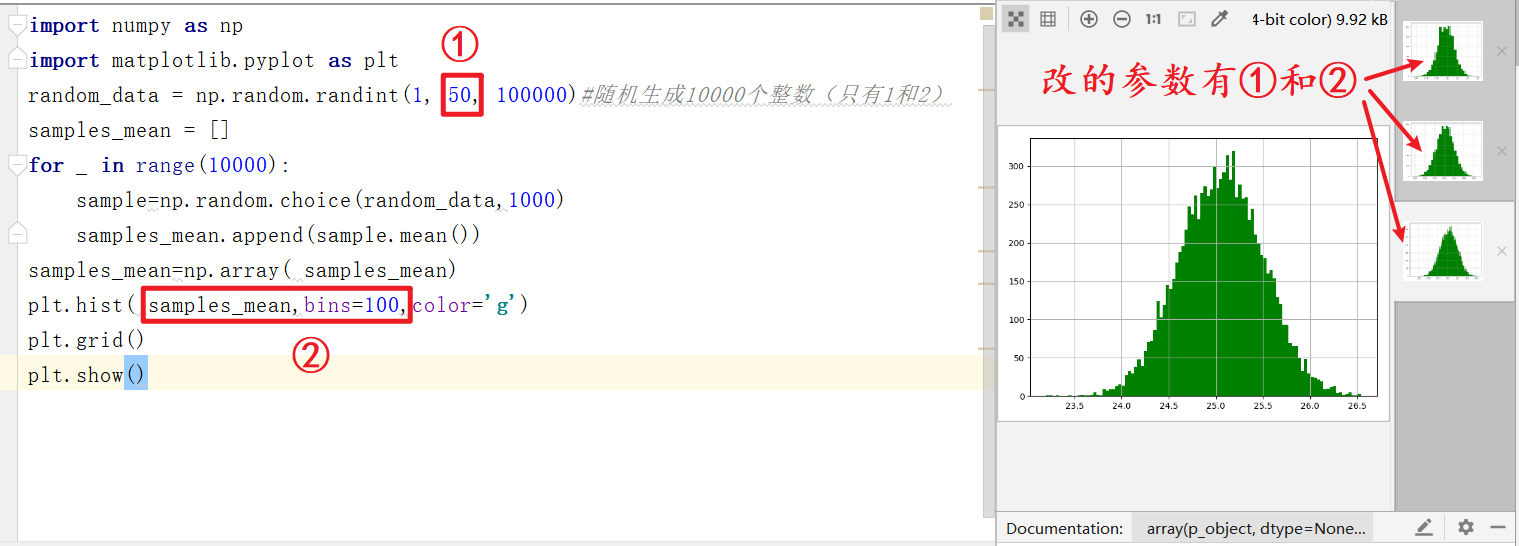
请对照后面的注释,看这段代码
import numpy as np
import matplotlib.pyplot as plt
random_data = np.random.randint(1, 50, 100000)#随机生成100000个整数,形成一个数组(1-49之间,不含50,左含右不含)
samples_mean = [] # 样本均值
for _ in range(10000):#此类语法见②
sample=np.random.choice(random_data,1000)#见①,从random_data数组中返回1000个数据,存入sample数组
samples_mean.append(sample.mean())#见③,给sample数组整体求均值,集齐9999个sample均值合成samples_mean数组
samples_mean=np.array(samples_mean)#见④,将Python的List对象,变为Numpy的ndarray对象
plt.hist(samples_mean,bins=100,color='g')#见⑤,直方图
plt.grid()#网格线
plt.show()#图形由show函数显示
①、choice(seq) 方法返回一个seq[可以是列表,元组或字符串]的随机项。
注意:choice()是不能直接访问的,需要导入 random 模块,然后通过 random 静态对象调用该方法。
np.random.choice(5,3)和np.random.randint(0,5,3)意思相同,表示从[0,5)之间随机以等概率选取3个数
②、for _ in range(10000)代表从0到9999循环
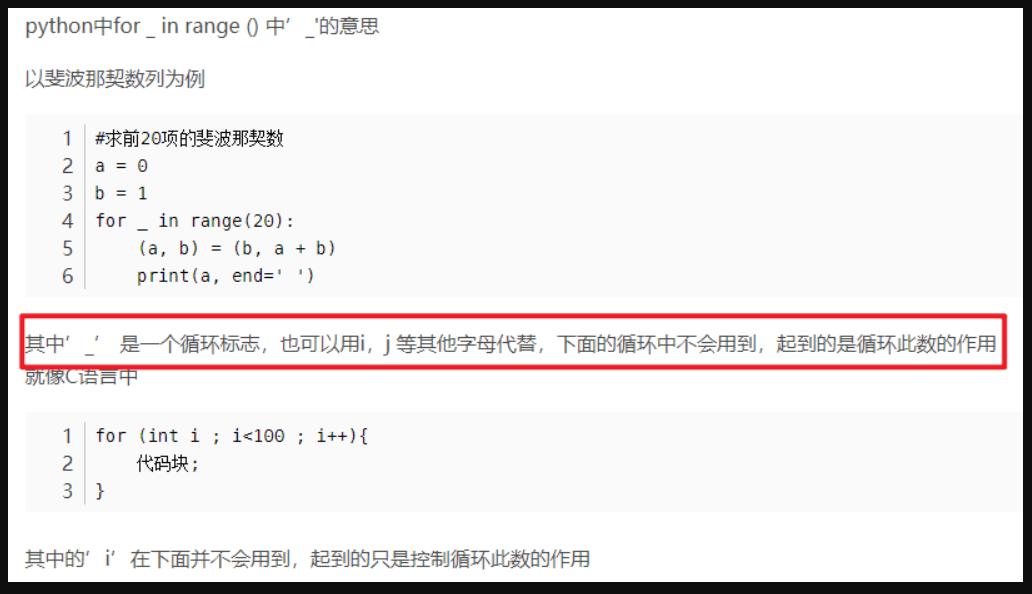
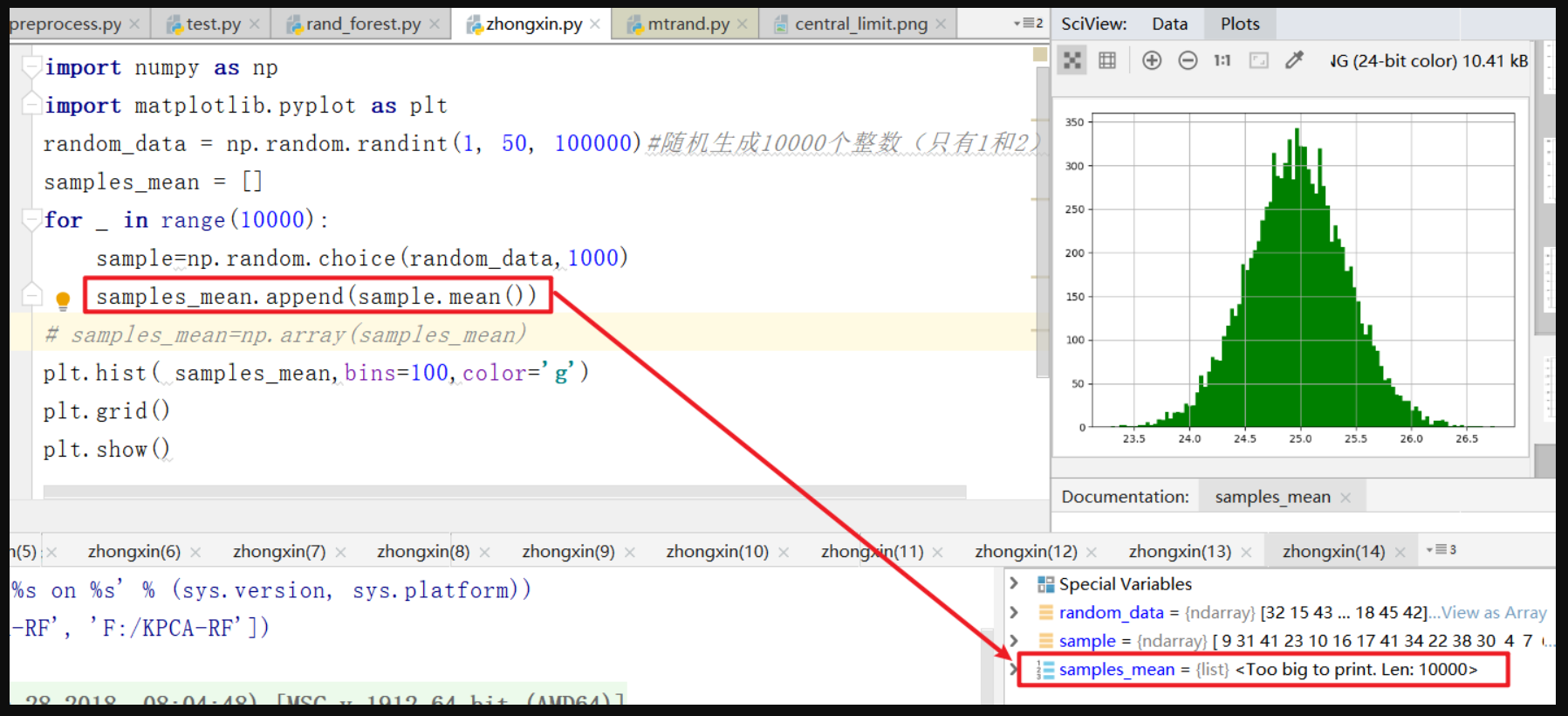
③、sample.mean()

④np.array(一维数组),有什么用呢
Numpy提供ndarray(N-dimensional array object)对象,存储单一数据类型的多维数组,节约内存和CPU,出自👉链接

如果你亲自使用,对比一下即可知道,用了np.array转换,明显感觉更快。在数值分析时,建议全部使用np的ndarray对象。

⑤plt.hist( x,bins=100,color='g')画直方图 👉官网说明文档
直方图与柱状图外观表现很相似,用来展现连续型数据分布特征的统计图形(柱状图主要展现离散型数据分布)
x: 数据集,最终的直方图将对数据集进行统计
bins=100:这个参数指定bin(箱子)的个数,也就是总共有几根树状条形图。
color:指定绿色用g和green都可以,源码里没说。用标准颜色就可以。

👉参考:plt.hist()与plt.hist2d()直方图和双直方图&matplotlib可视化篇hist()--直方图
后文写的更好,参数介绍的更全
后来经过讨论,还是认为,中心极限定理用python来证明,用random随机抛色子就好,不用像数学公式一样去证明

绘制ROC曲线和计算AUC值
ROC、AUC的简要介绍
这一小部分介绍出自公众号“数据蛙DataFrog”-作者:wing努力学习
数据分析师常见面试题--机器学习算法篇
https://mp.weixin.qq.com/s/mrUP4XT7m28u_36sRGqOHA
一、模型评估
1.1 什么是ROC曲线
ROC的全称是Receiver Operating Characteristic Curve,中文名字叫“受试者工作特征曲线”,顾名思义,其主要的分析方法就是画这条特征曲线。这里在网上找了一个比较好的图样示例如下:
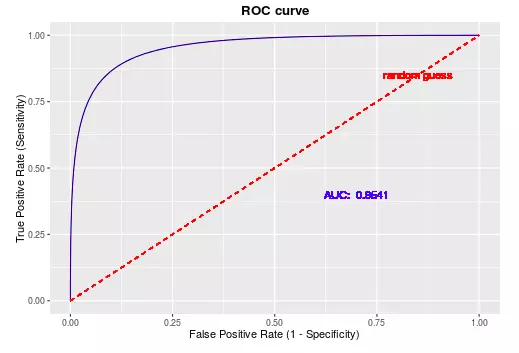
该曲线的横坐标为假阳性率(False Positive Rate, FPR),N是真实负样本的个数,FP是N个负样本中被分类器预测为正样本的个数。纵坐标为真阳性率(True Positive Rate, TPR),公式为:
P是真实正样本的个数,TP是P个正样本中被分类器预测为正样本的个数。
举一个简单的例子方便大家的理解,假设现在有10个雷达信号警报,其中8个是真的轰炸机(P)来了,2个是大鸟(N)飞过,经过某分析员解析雷达的信号,判断出9个信号是轰炸机,剩下1个是大鸟,其中被判定为轰炸机的信号中,有1个其实是大鸟的信号(FP=1),而剩下8个确实是轰炸机信号(TP=8)。
因此可以计算出FPR0.5,TPR为1,而就(0.5,1)对应ROC曲线上一点。
1.2 如何计算AUC
AUC(Area Under roc Cure),顾名思义,其就是ROC曲线下的面积,该值能够量化地反映基于rOC曲线衡量出的模型性能。
计算AUC值只需要沿着ROC横轴做积分就可以,取值一般在0.5~1之间。AUC越大,说明分类效果越好。
一键生成AUC-ROC-score得分的函数
另外我在研究自己的随机森林毕设的时候,发现一个可以直接生成AUC - ROC得分的函数
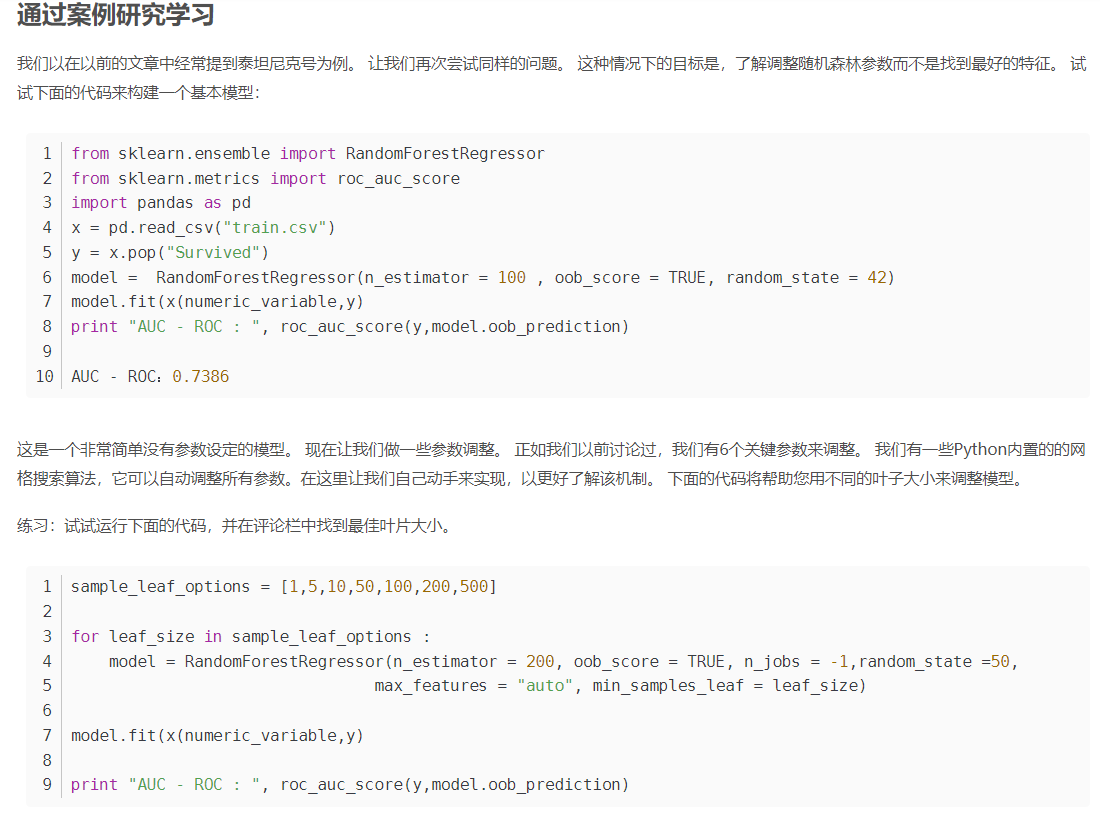
Python1的语法,需要用的自己改一改
print"AUC - ROC : ", roc_auc_score(y,model.oob_prediction)
对“文艺数字君”文章的研究
下面部分是看的这篇文章。👉ROC曲线的绘制与AUC的计算-文艺数字君👍
是对这篇文章的解析。
注意哟,本文的甲状腺病例图,和另外一个生病图是不一样的判断标准
甲状腺是低于V4-Value的认为是生病,样本病例图认为是高于threshold阈值为生病
甲状腺功能异常(Hypothyroid)和甲状腺功能正常(Euthyroid)
因为文章有说:我们假设T4 Value<5的时候, 认为是甲状腺功能异常(Hypothyroid)
所以,我们读者应该有这种意识:低于T4 Value的,全认为他有病。
Sensivity(Recall/TPR/True Positive Rate) 敏感性(召回/TPR/真阳性率)👉代表被判断为有病的人。实际是因为抬高了判断线,于是认为更多人得病了。
这里原文写错了:
原:通常会取一个阈值,使值大于黑线(在黑色线右侧)为Disease,在黑色线左侧表示Nomal.
改:通常会取一个判断黑线,使值大于黑线(在黑色线右侧)判断为有病,在黑色线左侧判断为没病/健康.


Specificity(特异性),翻译的看不懂,但从预备知识的公式和图可以看出来👇


因此,在我们甲状腺这个场景中
Specificity指的是,属实的健康人占整体健康人的比例。就叫他"属实健康率"吧。
因为文章后面做了一个小变换(FPR=1-Specificity,FPR假阳性率),那FPR就是,被误诊的健康人占整体健康人的,也就是“健康人误诊率”啦。

Sensivity(Recall/TPR/True Positive Rate真阳性率),TPR(被查出来的病人占总病人的比例),那TPR就是“已查明的病患率”啦

FPR假阳性率----对应-----健康人误诊率
TPR真阳性率----对应-----已查明的病患率
上面这种图比较重要,解释这么多,是因为涉及理解下面的TPR=FPR=1和0。
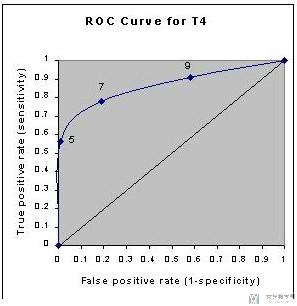
这副图像的横纵坐标是通过调整不同的阈值,计算出TPR与FPR得到的。对于坐标(1,1)和坐标(0,0)我们可以理解为:
- 当阈值T4 Value我们调整为最大的时候,这个时候就是全部预测为甲状腺功能异常(Hypothyroid),此时的TPR=FPR=1;
- 当阈值T4 Value我们调整为最小的时候,这个时候就是全部预测为甲状腺功能正常(Euthyroid),此时的TPR=FPR=0;
于是结合两个指标的意思,就能理解了。
我们也可以通过下面的图进行理解,如果正负样本是完全分离的,那么ROC曲线绘制出来就是两条直线的拼接,如下图所示:
我把原文的图改了一下。希望没错,如果出错了,请直接联系我哟。
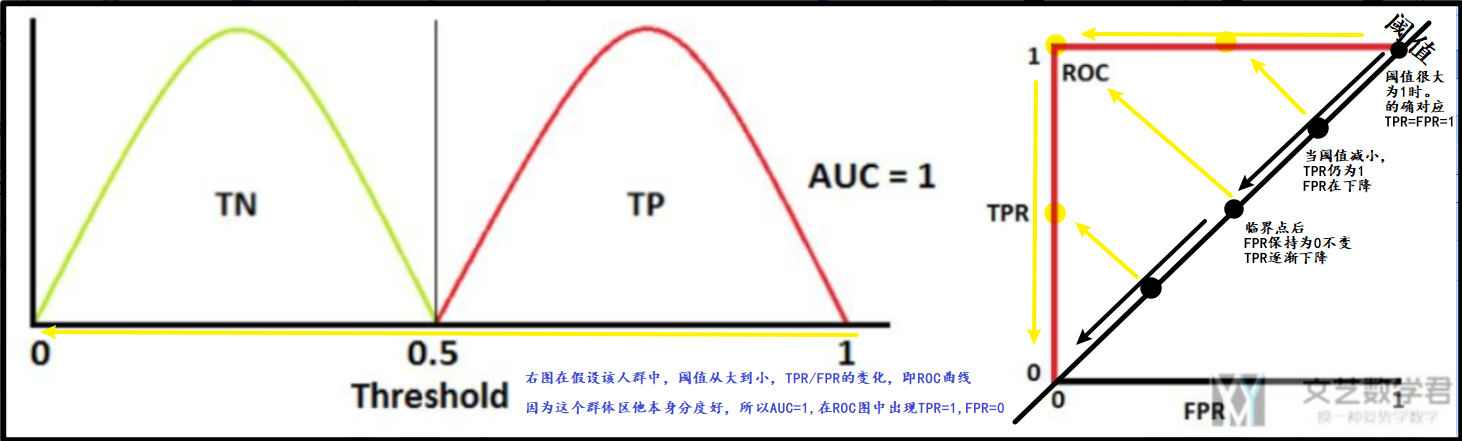
原文这个图下面的那句话应该是都写错了,所以就不要管了,知道ROC是代表TPR和FPR根据threshold的走势就行。
原文这句话应该是对的,我作图解释一下
当阈值(Threshold)调整的很大的时候,此时TPR=FPR=1。当阈值逐渐减小,我们希望我们的模型TPR=1, 但是FPR可以下降。当到了临界点的时候,此时FPR的值保持不变,TPR的值逐渐下降。
并且因为区分的很好,所以AUC在这个时候=1,【阈值=0.5,ROC曲线为直角,病人和健康人完全被划分开来的时候】
最后,我们终于知道,ROC是代表TPR和FPR根据threshold的走势
那么,AUC的值就是ROC曲线的下半部分占全体的比例。AUC值理解为区分度,即区分模型【在这个阈值时】对于正常样本与异常样本的区分度。
AUC值越大,即当前阈值情况下的ROC曲线区分度越好
可以看到,这个原文里的代码,展示了很多个(有5个)二分类器。分别是宏观平均ROC曲线/微观平均ROC曲线/第0类ROC曲线/第1类ROC曲线/第2类ROC曲线
这些都是ROC曲线,并都已经把AUC值求出来了(area就是AUC,区分度)

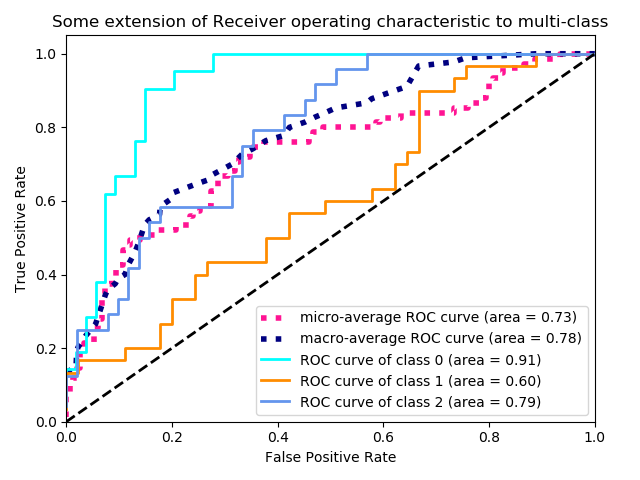
ROC、AUC的详细代码
最后贴一下原文章的代码整合,这段代码可以直接画出5种ROC曲线。
如果Plot all ROC curves这段代码删掉,那就会直接画出ROC曲线。
【这个直接画出来的ROC曲线有什么意义我得问一下原作者,还有宏观平均ROC曲线的意义他也没说】
看了代码后,我发现单独画出来的ROC曲线是第二种分类的ROC曲线
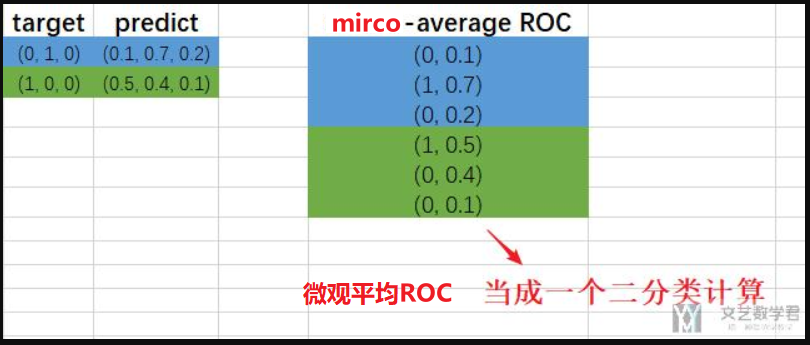
经过原博主的解释,我懂啦,micro-average ROC(微观平均)是把所有分类全部展开重新计算ROC,看成一个大的二分类来计算平均值(ROC曲线的平均和AUC值的平均)
macro-average ROC(宏观平均)是把三个分类分别拟合出三条ROC曲线,接着给定一组FPR(假阳性率),用拟合出的三个ROC去预测TPR,最后求平均,得出ROC曲线的平均和AUC值的平均
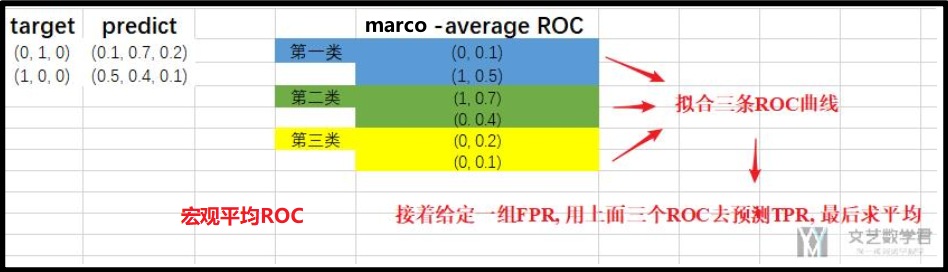
这是两种对多分类问题求平均的方式,看那个效果好,用那个(AUC值高的那个区分度好,效果好)
因为我没有亲自做过快手的笔试题,所以就直接把原博主解释过的官方ROC代码放在这边的,希望考试的小伙伴可以自己改编改编做出来哟。
import numpy as np
import matplotlib.pyplot as plt
from itertools import cycle
from sklearn import svm, datasets
from sklearn.metrics import roc_curve, auc
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import label_binarize
from sklearn.multiclass import OneVsRestClassifier
from scipy import interp
# Import some data to play with
iris = datasets.load_iris()
X = iris.data
y = iris.target
# Binarize the output
y = label_binarize(y, classes=[0, 1, 2])
n_classes = y.shape[1]
# Add noisy features to make the problem harder
random_state = np.random.RandomState(0)
n_samples, n_features = X.shape
X = np.c_[X, random_state.randn(n_samples, 200 * n_features)]
# shuffle and split training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.5,
random_state=0)
# Learn to predict each class against the other
classifier = OneVsRestClassifier(svm.SVC(kernel='linear', probability=True,
random_state=random_state))
y_score = classifier.fit(X_train, y_train).decision_function(X_test)
# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i])
roc_auc[i] = auc(fpr[i], tpr[i])
# 这个AUC值
print(roc_auc)
# Compute micro-average ROC curve and ROC area
fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_score.ravel()) # 这个是ROC曲线的坐标
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"]) # 这个是计算AUC的值
print(roc_auc)
# micro-average ROC(这个相当于是把所有的分类全部展开重新计算ROC, 看成一个大的二分类的结果)
# Compute macro-average ROC curve and ROC area
# First aggregate all false positive rates
all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)]))
# Then interpolate all ROC curves at this points
mean_tpr = np.zeros_like(all_fpr)
for i in range(n_classes):
mean_tpr += interp(all_fpr, fpr[i], tpr[i])
# Finally average it and compute AUC
mean_tpr /= n_classes
fpr["macro"] = all_fpr
tpr["macro"] = mean_tpr
roc_auc["macro"] = auc(fpr["macro"], tpr["macro"])
plt.figure()
lw = 2 # linewidth(线条的粗细)
plt.plot(fpr[2], tpr[2], color='darkorange',
lw=lw, label='ROC curve (area = %0.2f)' % roc_auc[2])
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--') # 这是绘制中间的直线
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()
# Plot all ROC curves
plt.figure()
plt.plot(fpr["micro"], tpr["micro"],
label='micro-average ROC curve (area = {0:0.2f})'
''.format(roc_auc["micro"]),
color='deeppink', linestyle=':', linewidth=4)
plt.plot(fpr["macro"], tpr["macro"],
label='macro-average ROC curve (area = {0:0.2f})'
''.format(roc_auc["macro"]),
color='navy', linestyle=':', linewidth=4)
colors = cycle(['aqua', 'darkorange', 'cornflowerblue'])
for i, color in zip(range(n_classes), colors):
plt.plot(fpr[i], tpr[i], color=color, lw=lw,
label='ROC curve of class {0} (area = {1:0.2f})'
''.format(i, roc_auc[i]))
plt.plot([0, 1], [0, 1], 'k--', lw=lw)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Some extension of Receiver operating characteristic to multi-class')
plt.legend(loc="lower right")
plt.show()
附网上一道ROC的题,已经很好理解啦




