协方差的意义

协方差其意义
协方差度量各个维度偏离其均值的程度。协方差的值如果为正值，则说明两者是正相关的；结果为负值就说明负相关的；如果为0，也是就是统计上的“相互独立”。

如果正相关，这个计算公式，每个样本对（Xi, Yi）,　每个求和项大部分都是正数，即两个同方向偏离各自均值，而不同时偏离的也有，但是少，这样当样本多时，总和结果为正。下面这个图就很直观。

在概率论中，两个随机变量 X 与 Y 之间相互关系，大致有下列3种情况：

 

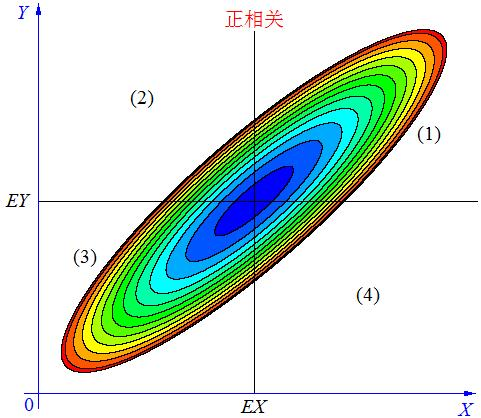
当 X, Y 的联合分布像上图那样时，我们可以看出，大致上有： X 越大  Y 也越大， X 越小  Y 也越小，这种情况，我们称为“正相关”。

 

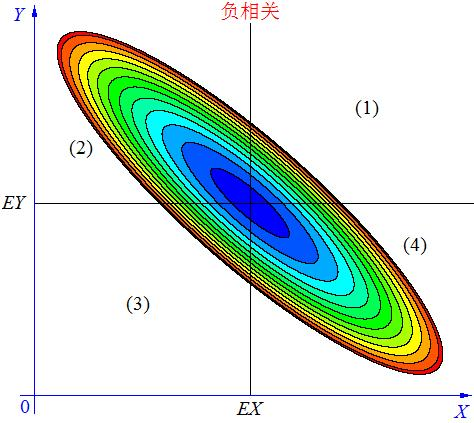
当X, Y 的联合分布像上图那样时，我们可以看出，大致上有：X 越大Y 反而越小，X 越小 Y 反而越大，这种情况，我们称为“负相关”。

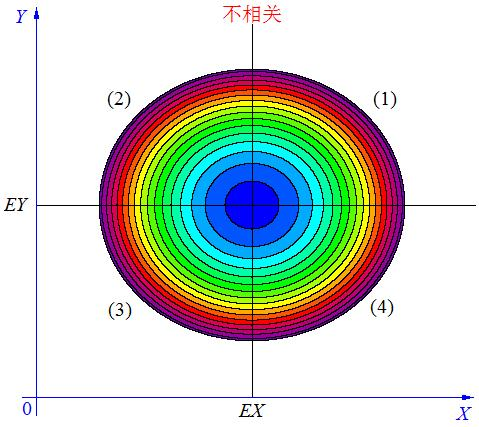
当X, Y  的联合分布像上图那样时，我们可以看出：既不是X  越大Y 也越大，也不是 X 越大 Y 反而越小，这种情况我们称为“不相关”。

在图中的区域（1）中，有 X>EX ，Y-EY>0 ，所以(X-EX)(Y-EY)>0；

在图中的区域（2）中，有 X<EX ，Y-EY>0 ，所以(X-EX)(Y-EY)<0；

在图中的区域（3）中，有 X<EX ，Y-EY<0 ，所以(X-EX)(Y-EY)>0；

在图中的区域（4）中，有 X>EX ，Y-EY<0 ，所以(X-EX)(Y-EY)<0。

当X 与Y 正相关时，它们的（联合）分布大部分在区域（1）和（3）中，小部分在区域（2）和（4）中，所以平均来说，有E(X-EX)(Y-EY)>0 。

当 X与 Y负相关时，它们的分布大部分在区域（2）和（4）中，小部分在区域（1）和（3）中，所以平均来说，有(X-EX)(Y-EY)<0 。

当 X与 Y不相关时，它们在区域（1）和（3）中的分布，与在区域（2）和（4）中的分布几乎一样多，所以平均来说，有(X-EX)(Y-EY)=0 。

所以，我们可以定义一个表示X, Y 相互关系的数字特征，也就是协方差
cov(X, Y) = E(X-EX)(Y-EY)。
当 cov(X, Y)>0时，表明 X与Y 正相关；

当 cov(X, Y)<0时，表明X与Y负相关；

当 cov(X, Y)=0时，表明X与Y不相关。

这就是协方差的意义。

 

如果数据是3维，那么协方差矩阵是

     

对角线上分别是x和y的方差，非对角线上是协方差。

（1）协方差大于0表示x和y若有一个增，另一个也增；

（2）协方差小于0表示一个增，一个减；

（3）协方差为0时，两者独立。

协方差绝对值越大，两者对彼此的影响越大，反之越小。