Treap

Treap介绍

概述

Treap是平衡树大家族的一员，是众多平衡树中最基础、最容易实现的，常数也不大。可以维护权值（常用）和区间。
Treap是Tree和Heap的合成词，其既有二叉查找树BST的性质，又有堆Heap的性质，于是有能维护排名，有能保证深度在\(\Theta(\log N)\)的量级

申明：本文借鉴于[【洛谷日报#119】浅析Treap](%3Ca href="http://www.360doc.com/content/19/0120/11/5315_810146183.shtml"%3Ehttp://www.360doc.com/content/19/0120/11/5315_810146183.shtml%3C/a%3E)

BST

概念

BST，即二叉查找树，是指对于任意节点，保证根左侧子树的所有节点比根小，右侧的所有节点比根大的树（没有相同节点），如图。

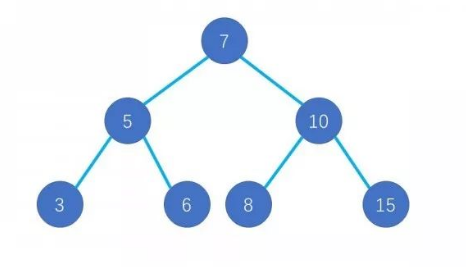
操作

查询x的排名

只要将x与根比较，如果相等，排名为左子树元素个数+1；
如果比根小，递归查询他在左子树的排名，排名为他在左子树的排名，空树排名为0；
如果比根大，递归查询他在右子树的排名，排名为右子树的排名+左子树元素个数+1

查询排名为x的数

先判断左子树元素个数是否大于等于x，
如果是就在左子树找，否则，如果刚好为左子树元素个数+1，就是根；
如果大于左子树元素个数+1，则必定在右子树。
思想和查询x的排名类似

插入x

我们不断地判断x与根的大小关系，
比根小，则递归左子树；比根大，则递归右子树，
直到来到一个空树，插入。

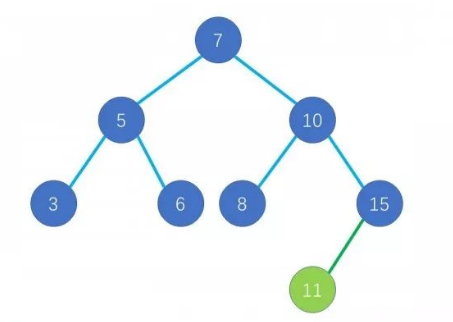
删除x

如果一个节点是叶子节点，直接删除；否则，如果这个节点有一个子节点，直接将其连接到该节点的父亲；否则，沿着右子树的根一路向左到底，然后用那个值替换掉要删除的节点。
例如我们要删7时，会选定8和7交换，然后递归删除7（注意8可能有右子树）

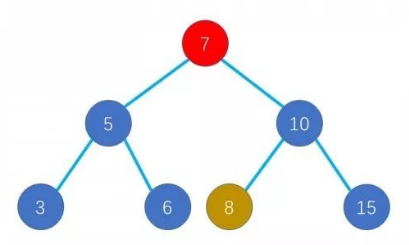
分析

BST支持Treap的所有一般操作，功能齐全，实现简单，在随机数据下也比Treap等平衡树快很多。

但BST毕竟不能维护树的平衡，BST的复杂度取决于它的平均深度，在特定数据下树会退化为链，使深度为线性，于是单次操作的复杂度会提升到\(\Theta(N)\)，明显不够优。

于是，我们需要引入Treap的下一个性质：Heap

Heap

概念

Heap，即堆，是一种保证任意节点的左右儿子都比自身小的完全二叉树，其深度始终保持在\(\log N\)的数量级，刚好符合了我们的需求

操作

查询

堆的根部即为最值，直接调取即可，但此处我们不需要用堆的这种性质。

插入

我们将新节点插入二叉树底端，

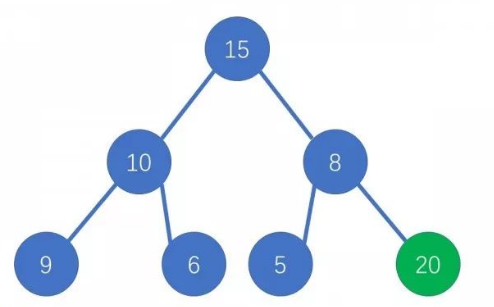
然后不断让新节点往上跳，直到它小于它的父亲或者自己为根

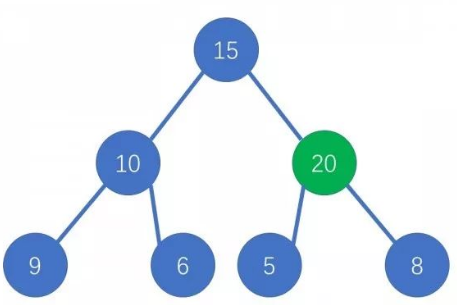
删除

我们用二叉树底端的节点覆盖根，然后让新的根与左右儿子比较，用较大的儿子替换根，如此往复即可

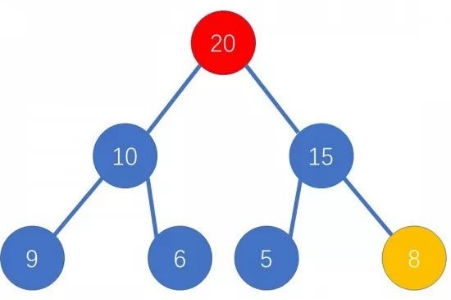
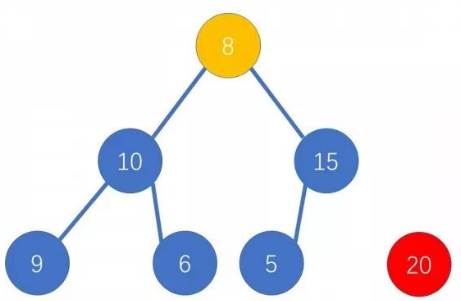
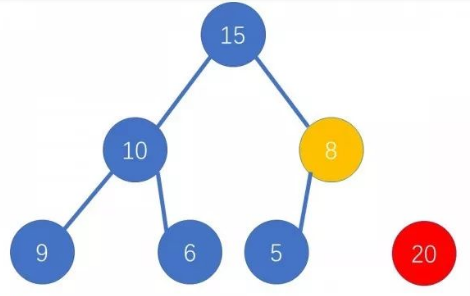
Treap

概念

Treap就是集BST、Heap二者的性质于一身，即能够支持BST的操作，有能够保证Heap的深度。

可惜的是，BST和Heap的性质似乎有些矛盾，前者是左子树<根<右子树，后者是根<左儿子<右儿子。

其实Treap的本质还是BST，对于任意节点，保证根左侧子树的所有节点比根小，右侧的所有节点比根大的树（没有相同节点）。我们只是利用堆的性质，赋予每一个节点一个随机值，按照随机值维护堆的形状。于是我们需要一个操作，既能保持BST的性质，又能够将根节点与儿子替换，于是我们需要Treap的核心——旋转操作

旋转

rotate，即旋转操作，分为zig左旋和zag右旋，其思想是一致的，也可以统一实现，故一起介绍
rotate的目标是将一个儿子移到根处，并且在此过程中保持BST的性质。此处我们以右旋为例讲述（举Luogu日报上的例子）

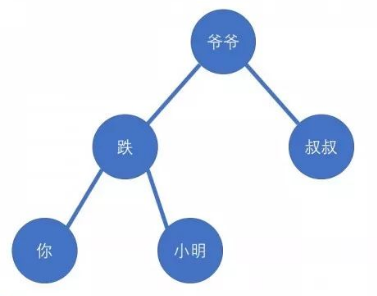
右旋以后效果为

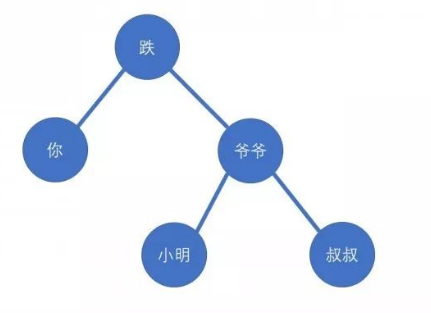
其中爹成功走到了爷爷辈，并使爷爷到了爹的子辈，符合Heap调整的需求，而此时在BST的大小关系上
旋转前：你<爹<小明<爷爷<叔叔
旋转后：你<爹<小明<爷爷<叔叔
于是BST的性质没变，我们就可以肆无忌惮地用rotate调整Heap了！

分析

于是，我们在BST的前提下保证了Heap的深度，单词操作复杂度为\(\Theta(\log N)\)，足够优秀

实现

初始化

size[i]——以i为根的子树的节点数
key[i]——i节点的关键字
cnt[i]——由于可能有重复，所以存储的是i节点关键字的个数
son[i][2]——存储i节点的儿子，son[i][0]表示左儿子，son[i][1]表示右儿子。
rd[i]——i节点的一个随机值，是在堆中的关键字？

`push_up`归并

顾名思义，拿儿子更新父亲p的节点数。p的节点数=左右儿子节点数之和+p本身存有数量

inline void push_up(int x){
	siz[x]=siz[son[x][0]]+siz[son[x][1]]+cnt[x];
}

`rotate`旋转

rotate(&p,d)——以p为根（可能有变）旋转，d=0左旋，d=1右旋

inline void rotate(int &x,int y){
	int ii=son[x][y^1];
	son[x][y^1]=son[ii][y];
	son[ii][y]=x;
	push_up(x);
	push_up(ii);
	x=ii;
}

让我们以d=0时左旋为例：

k=p的右儿子（暂时保存）

p的右儿子变成k的左儿子

        A(p)                         
       / \              
      B   D   C(k)               
               \              
                E

k的左儿子变成p

        C(k)
       / \
   (p)A   E
     / \   
    B   D

然后先pushup子代p的，再pushup父代k的

最后换根即可

        C(p)
       / \
      A   E
     / \   
    B   D

`insert`插入

ins(&p,x)——根为p，插入节点x

void ins(int &p,int x){
	if(!p){
		p=++sz;
		siz[p]=cnt[p]=1;
		key[p]=x;
		rd[p]=rand();
		return;
	}
	if(key[p]==x){
		cnt[p]++;
		siz[p]++;
		return;
	}
	int d=(x>key[p]);
	ins(son[p][d],x);
	if(rd[p]<rd[son[p][d]])
		rotate(p,d^1);
	push_up(p);
}

分类讨论

p==0，也就是说当前是一个空节点，
那么节点总数++，然后开辟一个新节点。
size[p]=1，共有1个节点在树中，
v[p]=x，值为x ，
num[p]=1，当前节点有一个重复数字，
rd[p]=rand()，生成随机值，拿来维护堆。
有一个数和要插入的x重复，那么直接个数加加即可
值可能在子树中，我们需要找一个子树，使得Treap的二叉排序树性质成立
以x>v[p]的情况为例
d=1，此时去p的右子树。
如果加完以后p的随机值小于它的右儿子，直接左旋调整，维护堆的性质
x<v[p]同理

`delete`删除

del(&p,x)——根为p，删掉节点x

void del(int &p,int x){
	if(!p)
		return;
	if(x!=key[p])
		del(son[p][x>key[p]],x);
	else{
		if(!son[p][0]&&!son[p][1]){
			cnt[p]--;
			siz[p]--;
			if(cnt[p]==0)
				p=0;
		}else if(son[p][0]&&!son[p][1]){
			/*Ö±½Óreplace£¿*/
			rotate(p,1);
			del(son[p][1],x);
		}else if(!son[p][0]&&son[p][1]){
			rotate(p,0);
			del(son[p][0],x);
		}else{
			int d=rd[son[p][0]]>rd[son[p][1]];
			rotate(p,d);
			del(son[p][d],x);
		}
	}
	push_up(p);
}

一个一个情况来看：

空节点，根本就没这个数，直接返回
如果x和v[p]不相等，直接去相应子树解决问题
如果x=v[p]
1. x是叶子节点，直接扣掉个数，如果个数为零删掉节点
2. 有一个子节点，直接把子节点旋转上来，然后去相应子树解决
3. 两个子节点，把大的那个转上来，然后去另一个子树解决

`rank`查询排名

rank(p,x)——根为p，查x在根为p的树中的排名

int get_rank(int p,int x){
	if(!p)
		return 0;
	if(key[p]==x)
		return siz[son[p][0]]+1;
	if(key[p]<x)
		return siz[son[p][0]]+cnt[p]+get_rank(son[p][1],x);
	/*if(key[p]>x)*/
	return get_rank(son[p][0],x);
}

空节点，直接返回掉
x==v[p]，那么左子树的全部数必定小于x，直接返回左子树节点数+1
x>v[p]，意味着x位于右子树，那么根和左子树一定比x小，先加上，然后再加上x在右子树里面的排名即可
x<v[p]，x位于左子树，冲向左子树解决

`find`按排名查询值

find(p,x)——根为p，查在根为p的子树中排名为x的数

int find(int p,int x){
	if(!p)
		return 0;
	if(siz[son[p][0]]>=x)
		return find(son[p][0],x);
	else if(siz[son[p][0]]+cnt[p]<x)
		return find(son[p][1],x-cnt[p]-siz[son[p][0]]);
	else
		return key[p];
}

如果是空节点，返回特殊值
左子树节点数大于x，解在左子树中
左子树加根的节点数比x小，解在右子树中，查右子树的第x-<左子树节点个数>-<根储存个数>名即可
左子树加根的节点大于等于x，意味着要找的就是当前的根节点v[p]

`pre`前驱

pre(p,x)——根为p，查在根为p的子树中x的前驱

int pre(int p,int x){
	if(!p)
		return -INF;
	if(key[p]>=x)
		return pre(son[p][0],x);
	else
		return max(key[p],pre(son[p][1],x));
}

空节点，没有前驱
如果x是根或在右子树，去左子树找
否则要么是根要么右子树，取一个max就可以了（前驱定义为小于x，且最大的数）

`suf`后继

su(p,x)——根为p，查在根为p的子树中x的后继

int suf(int p,int x){
	if(!p)
		return INF;
	if(key[p]<=x)
		return suf(son[p][1],x);
	else
		return min(key[p],suf(son[p][0],x));
}

与前驱超级类似

空节点无后继
如果在根或者左子树，去右子树找
否则要么根要么左子树，取min就可以了(后继定义为大于x，且最小的数)

例题

模板题：[P3369 【模板】普通平衡树](%3Ca href="https://www.luogu.org/problem/P3369"%3Ehttps://www.luogu.org/problem/P3369%3C/a%3E)

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int INF=1e9+7,MAXN=1e5+10;
int sz,rt;
int siz[MAXN],key[MAXN],cnt[MAXN],rd[MAXN],son[MAXN][2];
inline void push_up(int x){
	siz[x]=siz[son[x][0]]+siz[son[x][1]]+cnt[x];
}
inline void rotate(int &x,int y){
	int ii=son[x][y^1];
	son[x][y^1]=son[ii][y];
	son[ii][y]=x;
	push_up(x);
	push_up(ii);
	x=ii;
}
void ins(int &p,int x){
	if(!p){
		p=++sz;
		siz[p]=cnt[p]=1;
		key[p]=x;
		rd[p]=rand();
		return;
	}
	if(key[p]==x){
		cnt[p]++;
		siz[p]++;
		return;
	}
	int d=(x>key[p]);
	ins(son[p][d],x);
	if(rd[p]<rd[son[p][d]])
		rotate(p,d^1);
	push_up(p);
}
void del(int &p,int x){
	if(!p)
		return;
	if(x!=key[p])
		del(son[p][x>key[p]],x);
	else{
		if(!son[p][0]&&!son[p][1]){
			cnt[p]--;
			siz[p]--;
			if(cnt[p]==0)
				p=0;
		}else if(son[p][0]&&!son[p][1]){
			rotate(p,1);
			del(son[p][1],x);
		}else if(!son[p][0]&&son[p][1]){
			rotate(p,0);
			del(son[p][0],x);
		}else{
			int d=rd[son[p][0]]>rd[son[p][1]];
			rotate(p,d);
			del(son[p][d],x);
		}
	}
	push_up(p);
}
int get_rank(int p,int x){
	if(!p)
		return 0;
	if(key[p]==x)
		return siz[son[p][0]]+1;
	if(key[p]<x)
		return siz[son[p][0]]+cnt[p]+get_rank(son[p][1],x);
	/*if(key[p]>x)*/
	return get_rank(son[p][0],x);
}
int find(int p,int x){
	if(!p)
		return 0;
	if(siz[son[p][0]]>=x)
		return find(son[p][0],x);
	else if(siz[son[p][0]]+cnt[p]<x)
		return find(son[p][1],x-cnt[p]-siz[son[p][0]]);
	else
		return key[p];
}
int pre(int p,int x){
	if(!p)
		return -INF;
	if(key[p]>=x)
		return pre(son[p][0],x);
	else
		return max(key[p],pre(son[p][1],x));
}
int suf(int p,int x){
	if(!p)
		return INF;
	if(key[p]<=x)
		return suf(son[p][1],x);
	else
		return min(key[p],suf(son[p][0],x));
}
int Q;
int main(){
	scanf("%d",&Q);
	while(Q--){
		int ii,jj;
		scanf("%d%d",&ii,&jj);
		switch(ii){
			case 1:{
				ins(rt,jj);
				break;
			}
			case 2:{
				del(rt,jj);
				break;
			}
			case 3:{
				printf("%d\n",get_rank(rt,jj));
				break;
			}
			case 4:{
				printf("%d\n",find(rt,jj));
				break;
			}
			case 5:{
				printf("%d\n",pre(rt,jj));
				break;
			}
			case 6:{
				printf("%d\n",suf(rt,jj));
				break;
			}
		}
	}
	return 0;
}

可以看到，Treap的代码比Splay简洁很多，评测时效率也略高

posted @ 2019-08-05 07:54 guoshaoyang 阅读(5521) 评论(1) 编辑收藏举报

刷新页面返回顶部

Treap

Treap介绍

概述

BST

概念

操作

查询x的排名

查询排名为x的数

插入x

删除x

分析

Heap

概念

操作

查询

插入

删除

Treap

概念

旋转

分析

实现

初始化

push_up归并

rotate旋转

insert插入

delete删除

rank查询排名

find按排名查询值

pre前驱

suf后继

例题

模板题：[P3369 【模板】普通平衡树](%3Ca href="https://www.luogu.org/problem/P3369"%3Ehttps://www.luogu.org/problem/P3369%3C/a%3E)

`push_up`归并

`rotate`旋转

`insert`插入

`delete`删除

`rank`查询排名

`find`按排名查询值

`pre`前驱

`suf`后继