悬线法

悬线法

介绍

悬线法用于找出矩阵中满足特定条件的最大的矩形，例如全1矩阵或交错矩阵，在NOIP以上都可以考。

悬线法的思想很简单，就是记录每个点向上延伸的最大长度，再算出延伸这么长时最左和最右的长度，然后相乘即可。

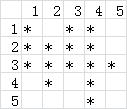
例如\((3,2)\)点向上可以延伸\(2\)格，向左、右分别可以延伸\(2,3\)格，最终的面积就是\(2\times(2+4-1)=8\)格；\((3,3)\)点向上可以延伸\(3\)格，向左、右分别可以延伸\(1,2\)格，最终的面积就是\(3\times(1+2-1)=6\)格。

正确性证明

我们断言，通过上面的测量一定可以找出最大解，我们只需要证明最大的矩形一定能够被访问。

如上图，任意一个外围的矩形都能被访问到，例如矩形\((1,3)(3,4)\)，点\((3,3)\)一定能够计算到；矩形\((2,1)(3,4)\)，点\((3,2)\)一定能够计算到。

例题

模板题：P4147 玉蟾宫

模板代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int INF=1e9+7,MAXN=1010;
int N,M,ans,a[MAXN][MAXN],up[MAXN][MAXN],lft[MAXN][MAXN],rt[MAXN][MAXN];
int main(){
	scanf("%d %d",&N,&M);
	for(int i=1;i<=N;i++){
		for(int j=1;j<=M;j++){
			char ch;
			scanf(" %c",&ch);
			a[i][j]=ch=='F';
		}
	}
	for(int i=1;i<=N;i++){
		for(int j=1;j<=M;j++){
			if(a[i][j]){
				up[i][j]=up[i-1][j]+1;
				lft[i][j]=lft[i][j-1]+1;
			}
			if(a[i][M-j+1]){
				rt[i][M-j+1]=rt[i][M-j+2]+1;
			}
		}
	}
	for(int i=1;i<=N;i++){
		for(int j=1;j<=M;j++){
			if(a[i][j]&a[i-1][j]){
				lft[i][j]=min(lft[i][j],lft[i-1][j]);
				rt[i][j]=min(rt[i][j],rt[i-1][j]);
			}
			ans=max(ans,(rt[i][j]+lft[i][j]-1)*up[i][j]);
		}
	}
	printf("%d",3*ans);
	return 0;
}

P1169 [ZJOI2007]棋盘制作

#include<iostream>
using namespace std;
const int SIZE=1024*2;
int n,m,a[SIZE][SIZE],squ[SIZE][SIZE],rect[SIZE][SIZE],max_squ,max_rect,l[SIZE][SIZE],r[SIZE][SIZE],up[SIZE][SIZE];
int main(){
	cin >> n >> m;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			up[i][j]=1;
			cin >> a[i][j];
			if((i+j)&1){
				a[i][j]=!a[i][j];
			}
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(i==1||j==1||a[i][j]!=a[i-1][j]||a[i][j]!=a[i][j-1]||a[i-1][j]!=a[i-1][j-1]){
				squ[i][j]=1;
			}else{
				squ[i][j]=min(squ[i-1][j-1],min(squ[i-1][j],squ[i][j-1]))+1;
			}
			if(squ[i][j]>max_squ){
				max_squ=squ[i][j];
			}
		}
	}
	cout << max_squ*max_squ << endl;
	for(int i=1;i<=n;i++){
		l[i][1]=1;
		for(int j=2;j<=m;j++){
			if(a[i][j]==a[i][j-1]){
				l[i][j]=l[i][j-1];
			}else{
				l[i][j]=j;
			}
		}
		r[i][m]=m;
		for(int j=m-1;j>=1;j--){
			if(a[i][j]==a[i][j+1]){
				r[i][j]=r[i][j+1];
			}else{
				r[i][j]=j;
			}
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(i>1&&a[i][j]==a[i-1][j]){
				l[i][j]=max(l[i][j],l[i-1][j]);
				r[i][j]=min(r[i][j],r[i-1][j]);
				up[i][j]=up[i-1][j]+1;
			}
			max_rect=max(max_rect,(r[i][j]-l[i][j]+1)*up[i][j]);
		}
	}
	cout << max_rect;
	return 0;
}