绝对值方程、不等式
- 概述
- 绝对值问题在中考中不超纲,并且解题过程繁杂,可以作为排位较后的题目考
- 解决这类问题的核心思想就是去绝对值,取绝对值的方法有
- 分类讨论
- 解决简单的问题可以用分类讨论,面对复杂问题时要分很多层,过程可能会很繁杂(怕死就多分类);但有时候在多层分类中能够获得特殊的条件,不用考虑某些情况
- 在解方程或不等式时,这种方法往往表述较为简单
- 函数思想
- 方程、不等式都可以转换为函数的关系,可以将绝对值的意义变为按照x轴或x=a翻折
- 这种方法比较适合 式子的一边已知并且含绝对值,另一边含参但结构简单 的问题
- 几何意义
- 当绝对值内主元的元素相同时:2个绝对值可以转化为1维距离,2个绝对值里含平方差可以转化为2维距离
- 分类讨论
- 注意:分类讨论之后一定要写“综上”,把解写出来
-
绝对值方程
-
一次方程
- 多个单层绝对值(零点分段法步骤)
- 找绝对值零点
- 写出使各个绝对值代数式为0的x值
- 零点分段讨论
- 将数轴分段,讨论
- 分段求解方程
- 在每一种分类讨论中解方程,再分别检验
- 例


- 找绝对值零点
- 单个多层绝对值
- 由内而外去绝对值符号
- 按照零点分段法一层层去绝对值,再检验
- 例

- 由外而内去绝对值符号
- 将单个绝对值放左边,将其他部分放另一边,右边的部分可以取正负
- 例


- 由内而外去绝对值符号
- 函数法
- 对于含参的方程,分类讨论比较困难,故可以将已知部分用函数表示,将问题转化为求交点
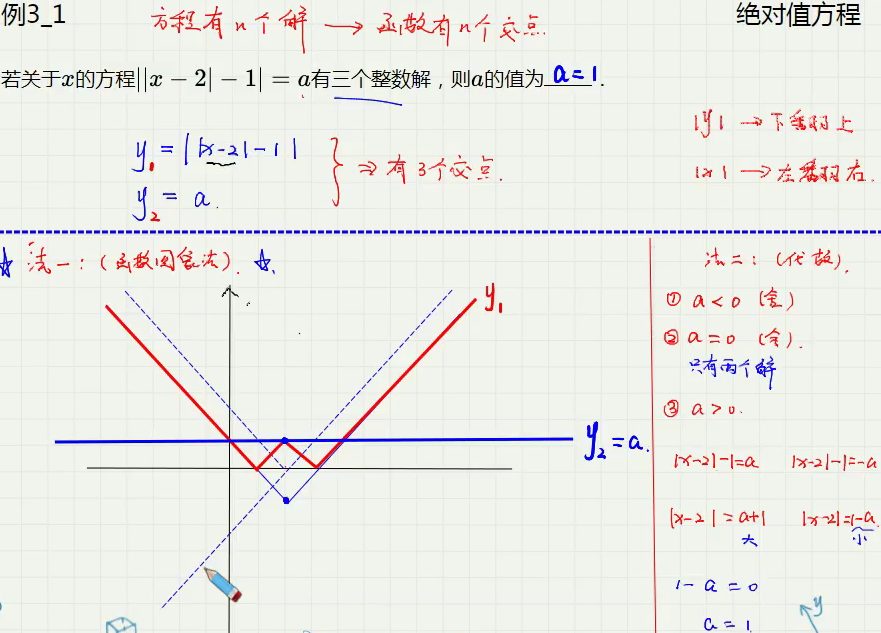
- 对于多个绝对值,要先写出分段函数,再画出函数

- 对于含参的方程,分类讨论比较困难,故可以将已知部分用函数表示,将问题转化为求交点
- 多个单层绝对值(零点分段法步骤)
-
二次方程
- 与一次方程同理,分别找零点,可以先因式分解
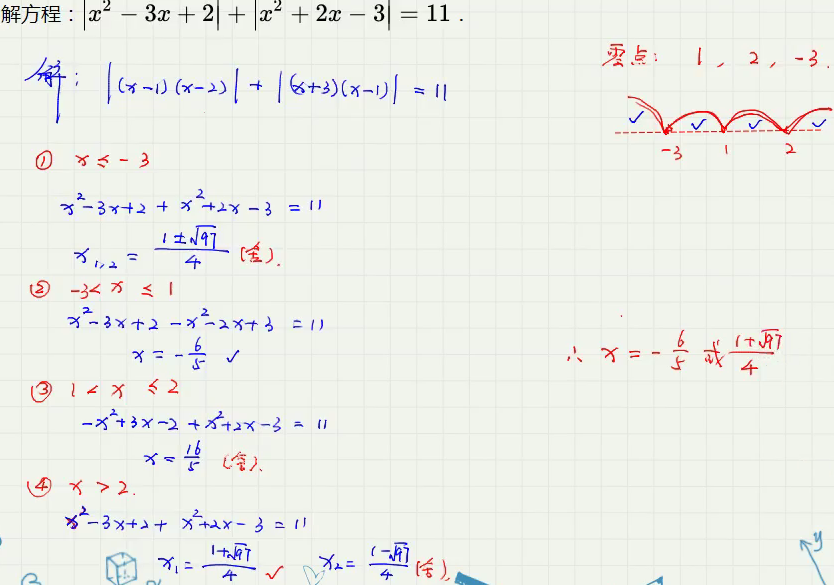
- 与一次方程同理,分别找零点,可以先因式分解
-
-
绝对值不等式
- 基本性质
-
$|a|\geq|b|\Leftrightarrow a\geq|b|$或$a\leq-|b|\Leftrightarrow-|a|\leq b \leq |a| $
-
$|a|-|b|\leq|a\pm b|\leq|a|+|b|$
-
- 直接平方法
- 绝对值的部分平方后可以忽略绝对值。例如
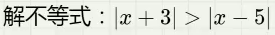
- 绝对值的部分平方后可以忽略绝对值。例如
- 分式法
- 对于$|a_1x^2+b_1x+c|=|a_2x+b_2|$,只要使$|a_2x+b_2|$不为零,就可以转化为$\displaystyle \frac{|a_1x^2+b_1x+c|}{|a_2x+b_2|}$,因式分解后可以化简
- 零点分段法
- 分类讨论
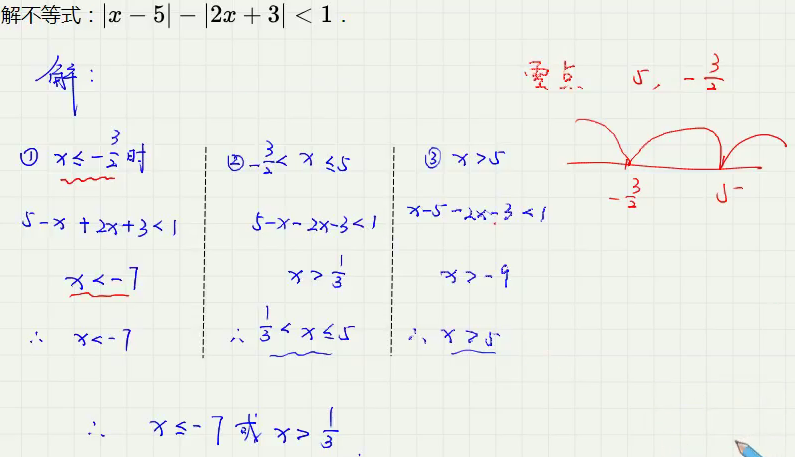


- 分类讨论
- 含参不等式
- 求条件不等式范围:分段考虑

- 几何意义


- 求条件不等式范围:分段考虑
- 基本性质



