洛谷P4027 [NOI2007]货币兑换
P4027 [NOI2007]货币兑换
算法:dp+斜率优化
题面十分冗长,题意大概是有一种金券每天价值会有变化,你可以在某些时间点买入或卖出所有的金券,问最大收益
根据题意,很容易列出朴素的状态转移方程:
设\(f_i\)为第\(i\)天B券的数量,\(ans_j\)为以当前价格卖光第\(j\)天的金券可获得的收益,则
\(f_i=\max{ans_j}/(a_i*r_i+b_i)\)
\(O(n)\)求\(\max{ans_j}\),复杂度为\(O(n^2)\)
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
typedef long long LL;
const int MAXN=1024*100;
int N;
double S,a[MAXN],b[MAXN],r[MAXN],f[MAXN],ans;
int main(){
scanf("%d%lf",&N,&S);
for(int i=1;i<=N;i++){
scanf("%lf%lf%lf",&a[i],&b[i],&r[i]);
}
ans=S;
f[1]=ans*r[1]/(a[1]*r[1]+b[1]);
for(int i=1;i<=N;i++){
for(int j=1;j<i;j++){
ans=max(ans,f[j]*a[i]+f[j]/r[j]*b[i]);
}
f[i]=ans*r[i]/(a[i]*r[i]+b[i]);
}
printf("%.3lf",ans);
return 0;
}
然而此题要求\(O(nlogn)\)的做法,故朴素的dp无法AC,此时可以想到斜率优化
step1:转化方程
设\(a_i\)为第\(i\)天A券的价格,\(b_i\)为第\(i\)天B券的价格,\(ca_i\)为第\(i\)天A券的数量,\(cb_i\)为第\(i\)天B券的数量,\(f_i\)为第\(i\)天的最大收益
则\(f_i=\max{ca_j*a_i+cb_j*b_i}\)
∴如果j比k更优,有
\(ca_j*a_i+cb_j*b_i>ca_k*a_i+cb_k*b_i\)
∴\((cb_j-cb_k)*b_i>-a_i*(ca_j-ca_k)\)
∴\(\frac{cb_j-cb_k}{ca_j-ca_k}>-\frac{a_i}{b_i}\)
以\(ca\)为横坐标\(cb\)为纵坐标建立如图所示平面直角坐标系
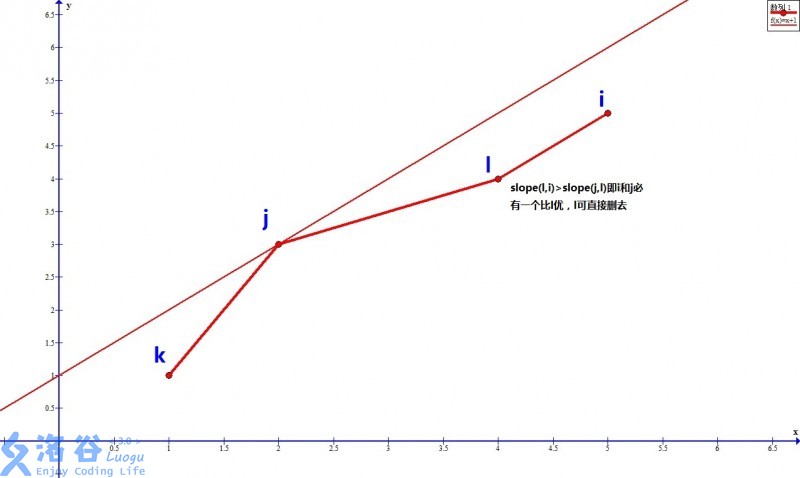
剩下的就可以-斜率优化-了
不过此题不比模板题,ca与cb不满足单调性,所以需要用平衡树或cdq等方法维护,此处用stl_set维护(因为是凸壳,所以斜率与横坐标同时满足单调性,可以用一个关键字查找)
此处切线只要找\(-\frac{a}{b}\)的lower_bound即可(代码中的query)
此处插入点要把当前位置两边的点都判断一下是否与上凸壳冲突,删除(代码中的insert)
实现就不难了
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
#include<set>
using namespace std;
typedef long long LL;
const int MAXN=1024*100;
int N;
double S,A[MAXN],B[MAXN],R[MAXN],F[MAXN],CA[MAXN],CB[MAXN];
inline double ABS(double x) { return x>0?x:-x; }
struct node {
double X,Y,K;
int flag;
node() { X=Y=K=flag=0; }
node(double x,double y) { X=x; Y=y; flag=0; }
friend inline bool operator<(node x,node y) {
if(x.flag||y.flag) { return x.K>y.K; }
return x.X<y.X;
}
friend inline bool operator==(node x,node y) { return ABS(x.X-y.X)<1e-8; }
friend inline double operator*(node x,node y) { return (y.Y-x.Y)/(y.X-x.X); }//斜率
inline bool error() { return X<-1e20||Y<-1e20; }
} error(-1e21,-1e21);
set<node> dq;
typedef set<node>::iterator ITER;
inline node next(node x) {
ITER ii=dq.upper_bound(x);
return ii==dq.end()?error:*ii;
}
inline node lower(node x) {
ITER ii=dq.lower_bound(x);
return ii==dq.end()?error:*ii;
}
inline node pre(node x) {
ITER ii=dq.lower_bound(x);
return ii==dq.begin()?error:*(--ii);
}
inline void insert(node x) {
if(dq.empty()) {
x.K=0;
dq.insert(x);
return;
}
node L=pre(x),R=lower(x);
if((L.error()&&x.Y<R.Y)||(!L.error()&&!R.error()&&L*x-L*R<1e-8)/**/||(x==R)) { return; }
R=next(x);
while(1) {
L=R;
R=next(L);
if(L.error()||R.error()||(x*L)-(L*R)>=1e-8) { break; }
dq.erase(L);
}
L=pre(x);
while(1) {
R=L;
L=pre(R);
if(L.error()||R.error()||(L*R)-(R*x)>=1e-8) { break; }
dq.erase(R);
}
L=pre(x);
R=next(x);
x.K=(L.error()?0:(L*x));
dq.insert(x);
if(!R.error()) {
dq.erase(R);
R.K=(x*R);
dq.insert(R);
}
}
inline double query(double x,double y) {
node ii;
ii.flag=1;
ii.K=-x/y;
ii=*(--dq.lower_bound(ii));
return ii.error()?0:ii.X*x+ii.Y*y;
}
int main() {
scanf("%d%lf",&N,&S);
for(int i=1; i<=N; i++) {
scanf("%lf%lf%lf",&A[i],&B[i],&R[i]);
}
F[1]=S;
CB[1]=S/(A[1]*R[1]+B[1]);
CA[1]=CB[1]*R[1];
insert(node(CA[1],CB[1]));
for(int i=2; i<=N; i++) {
F[i]=max(F[i-1],query(A[i],B[i]));
CB[i]=F[i]/(A[i]*R[i]+B[i]);
CA[i]=CB[i]*R[i];
insert(node(CA[i],CB[i]));
}
printf("%.3lf",F[N]);
return 0;
}


