常见物理量测量方法

1. 概述
   1. 物理实验主要分为探究实验和测量实验，本章将会讲述常用的测量技巧
   2. 测量的方法分为直接测量好间接测量，直接测量很简单，但很重要（不要忘了用），间接测量方法较多，主要思想是等效替代
   3. 在测量的过程中要尽可能减小误差，常见的方法有
      1. 选用更精密的工具
      2. 使用特殊测量方法
         1. 做差法
         2. 积累法，（（称）大算小）
      3. 多次测量去平均值
2. 长度
   1. 精度
      1. 读到分度值下一位，则知道精度可以反推分度值
   2. 测量偏大（小）
      1. 尺子膨胀或拉伸则测量偏小，尺子收缩则测量偏大
      2. 尺子分度值标错位、分度值错（但刻度均匀）
      3. 1. 比例法
         2. 列方程或计算分度值（迫不得已）
   3. 特殊长度测量方法
      1. 积累法
      2. 以直代曲法
      3. 滚轮法
      4. 1. 改装大的车轮容易超速（仪表盘没有变）
      5. 间接测量
         1. 通过质量
            1. 用天平和米尺测出一卷铁丝的长度（允许剪断）
         2. 通过面积
            1. 用刻度尺测出一卷卷纸的长度
               1. 测出外圈和内圈的半径
               2. $L=\frac{R^2-r^2}{d}$
3. 体积
   1. 刻度尺、量筒
      1. 吸水、溶于水
         1. 置换溶液
            1. 用沙子
            2. 用不吸、溶解的液体（油）
         2. 使溶液饱和（防止溶解）
            1. 加糖、盐
         3. 将物体吸满水（防止吸水）
         4. 用刻度尺量规则形状的物体
         5. Example
            1. 用方糖、尺子、量筒、玻璃棒、水测量方糖的体积
               1. 将方糖碾碎放入量筒
               2. 在水中放糖，用量筒
               3. 用刻度尺测长宽高
            2. 测肥皂密度
               1. 切下一块规则形状的肥皂测量
   2. 计算
      1. $\rho=\frac{m}{V}$
      2. 阿基米德原理
4. 质量
   1. 偏大（小）
   2. 杠杆
      1. 不等臂
         1. 将物体放在两端分别称量得到结果$m_1,m_2$
         2. $m=\sqrt{m_1m_2}$
      2. 测游码质量
         1. 游码刻度$m$标尺对应长度为$l_1$，托盘力臂为$l_2$
         2. 则游码质量为$\frac{l_2m}{l_1}$
      3. 杆秤

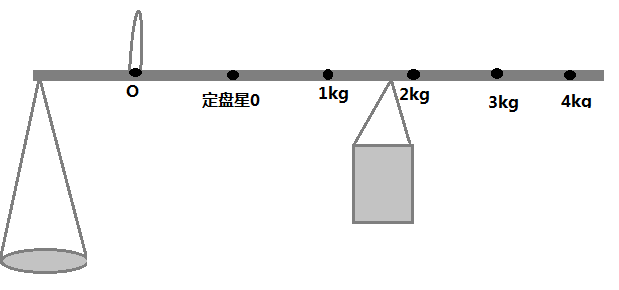
         不等臂，刻度均匀，重心在支点左侧

         1. 如图，左盘离支点$10cm$，定盘星离支点$5cm$，杆秤的标准秤砣质量为$1kg$，实际用了$2kg$的秤砣，测得$1.8kg$则问题实际质量为多少？
            
            1. 设横梁质量$M'$，力臂$L'$，$1.8kg$处力臂为$L''$，物体质量$m_x$
            2. 将原秤砣放在定盘星处，得$$M'gL'=1kg\times g\times 5cm$$
               
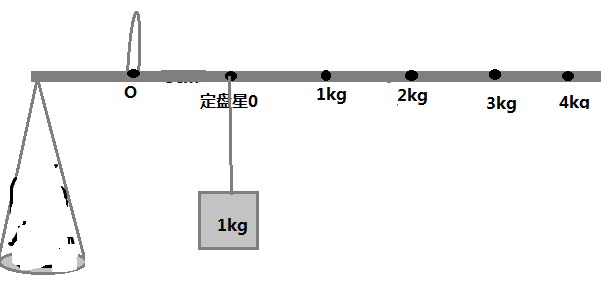
            3. 将原秤砣移至$1.8kg$处，得$$1.8kg\times g\times 10cm+M'gL'=1kg\times g\times L''$$
               
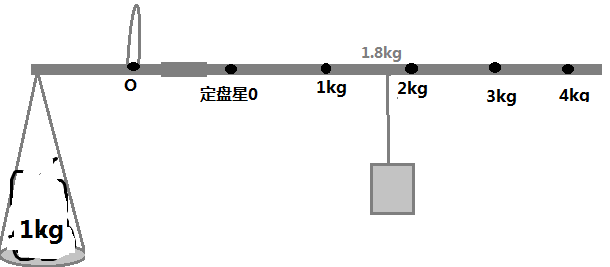
            4. $2kg$的秤砣置于$1.8kg$处，得$$m_x\times g\times 10cm+M'gL'=2kg\times g\times L''$$
               
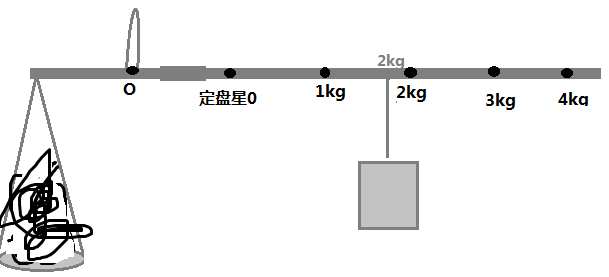
            5. 解得$m_x=4.1kg$
      4. 物理天平
          
         
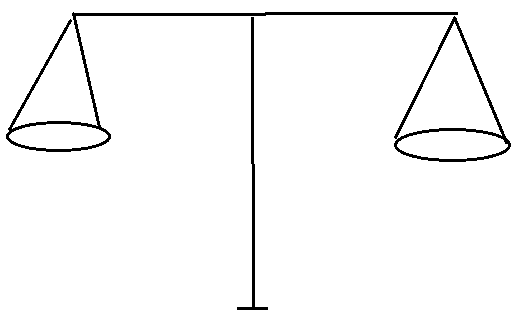
         1. 与弹簧测力计类似，一端可以伸进任何地方
   3. 天平状态
      1. 超重、失重
         1. 向上有加速度：超重
         2. 向下游加速度：失重
      2. 完全失重
         1. 空间站无动力巡航：重力全部用于向心力，此时天平无法称量
5. 密度
   1. 天平+量筒
   2. 称重法测液体密度
      1. 将大密度固体悬空测出重力，再浸入液体中测出重力
   3. 漂浮法
      1. 将柱形固体漂浮在液体内，测出固体的高和浸入水中的深度。则已知任意一个密度即可求出另一个
   4. 压强法
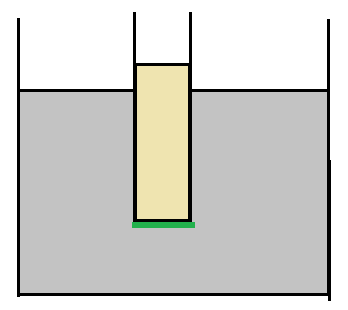      1. 测量帽子刚脱离时两侧液面高度
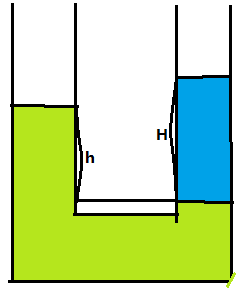      2. 根据连通器原理，密度之比等于高度之比的倒数
   5. 杠杆法
      1. 如图棍子$\frac{3}{4}$浸入水中，求其密度
         
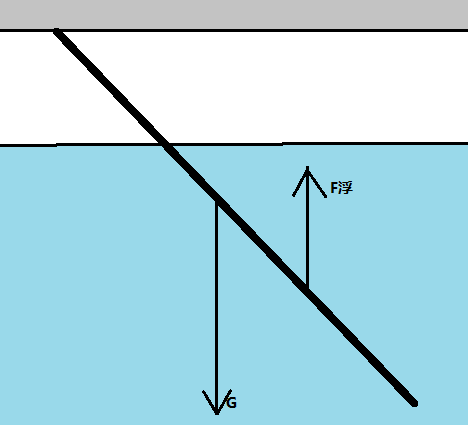
         1. $$\frac{G}{F_{浮}}=\frac{L_{浮}}{L_G}=\frac{\frac{5}{8}}{\frac{1}{2}}=\frac{5}{4}$$
         2. $$\frac{\rho\times s\times L\times g}{\rho_{水}\times \frac{3}{4}\times s\times L\times g}=\frac{5}{4}$$
         3. $$\rho=\rho_{水}\times \frac{3}{4}\times \frac{5}{4}=\frac{15}{16}$$