对称电路
- 概述
- 初中课内学的电学只包括简单电路,即只有单一串并联关系,没有环的电路。但事实上大多数电路并没有这个性质,其中中学阶段的大多数电路都可以通过对称电路的等效变换转化回简单电路。
- 目录
名字是我瞎编的,有专业的学名- 轴对称电路
- 中心对称电路
- 此处的分析都是局部分析,在整个电路中,可以将任意一个局部按照这种方法分析
- 轴对称电路
- 判定
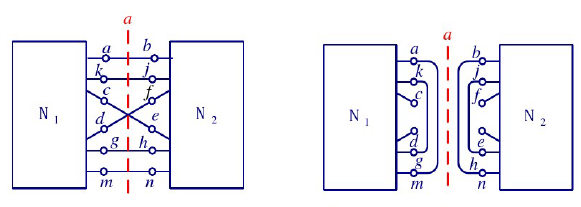
- 这种电路的学名叫做具有翻转对称性质的网络,即某轴线两段的电路是等价的,可以通过翻折重合
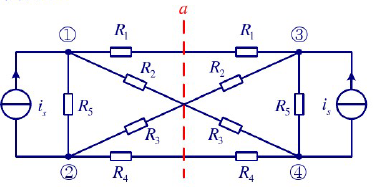 如图,整个网络关于直线$a$成轴对称,则它就是轴对称电路
如图,整个网络关于直线$a$成轴对称,则它就是轴对称电路
- 这种电路的学名叫做具有翻转对称性质的网络,即某轴线两段的电路是等价的,可以通过翻折重合
-
性质
-
对于轴对称电路,我们将不交叉的部分变成开路,交叉部分短路

-
- 应用
 的等效电路图是
的等效电路图是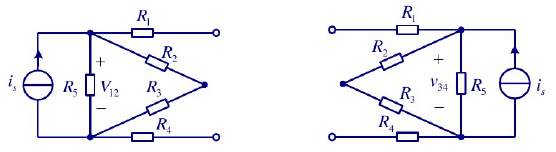
- 求等效电路图
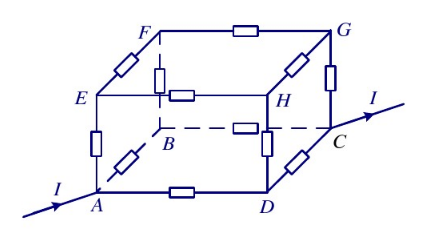
- 将俯视图拉伸得
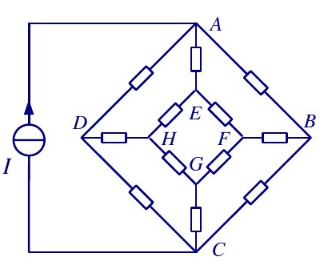
- 将轴线上的电阻拆成并联的倍值电阻
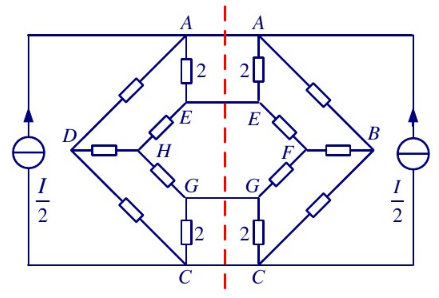
- 轴对称电路分析得
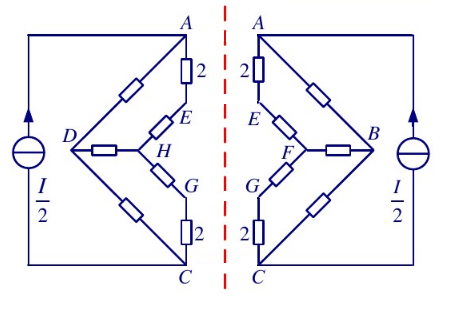
- 将俯视图拉伸得
- 判定
- 中心对称电路
- 判定
- 若一个电路关于某一点中心对称,即网络的一部分绕某一点旋转$180^{\circ}$与另一部分重合,则称此网络为中心对称电路
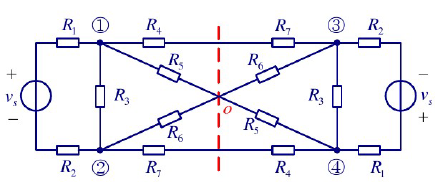
- 若一个电路关于某一点中心对称,即网络的一部分绕某一点旋转$180^{\circ}$与另一部分重合,则称此网络为中心对称电路
- 性质
- (和轴对称的性质相反)将原网络的平行线断开后连上下颠倒的线,将交线断开后保持开路
- 证明
- 其实中心对称电路是轴对称电路的一种特殊应用,其性质是轴对称电路性质的推论
- 首先将中心对称电路一侧的网络以过中心的水平线为轴翻折
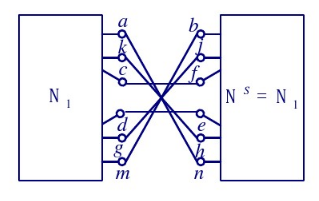
- 然后网络就变成了轴对称电路,直接分析就可以了
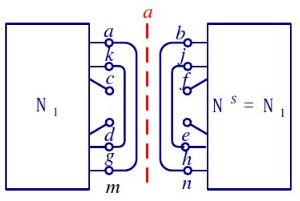
- 应用
 的等效电路是
的等效电路是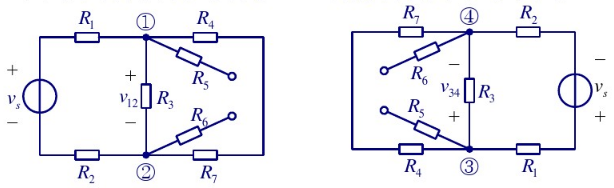
- (和轴对称的性质相反)将原网络的平行线断开后连上下颠倒的线,将交线断开后保持开路
- 判定


