FFT快速傅里叶变换

快速傅里叶变换FFT

参考文献:《算法导论》

多项式

 

定义：

 

 

多项式加法：

 

多项式乘法：

 

多项式的系数表达：

 

 

多项式值的点值表达：

 

 

插值（将点值还原成多项式）：

已知的将点值转换为多项式系数的方法有高斯消元（$\Theta(N^3)$）、拉格朗日插值法（$\Theta(N^2)$）等，但通过类似于求点值的方法，可以将复杂度降到$\Theta(N*logN)$

 

点值的作用：

 

快速乘法：（其中单位复数根接下来会介绍，此处不必纠结）

 

 

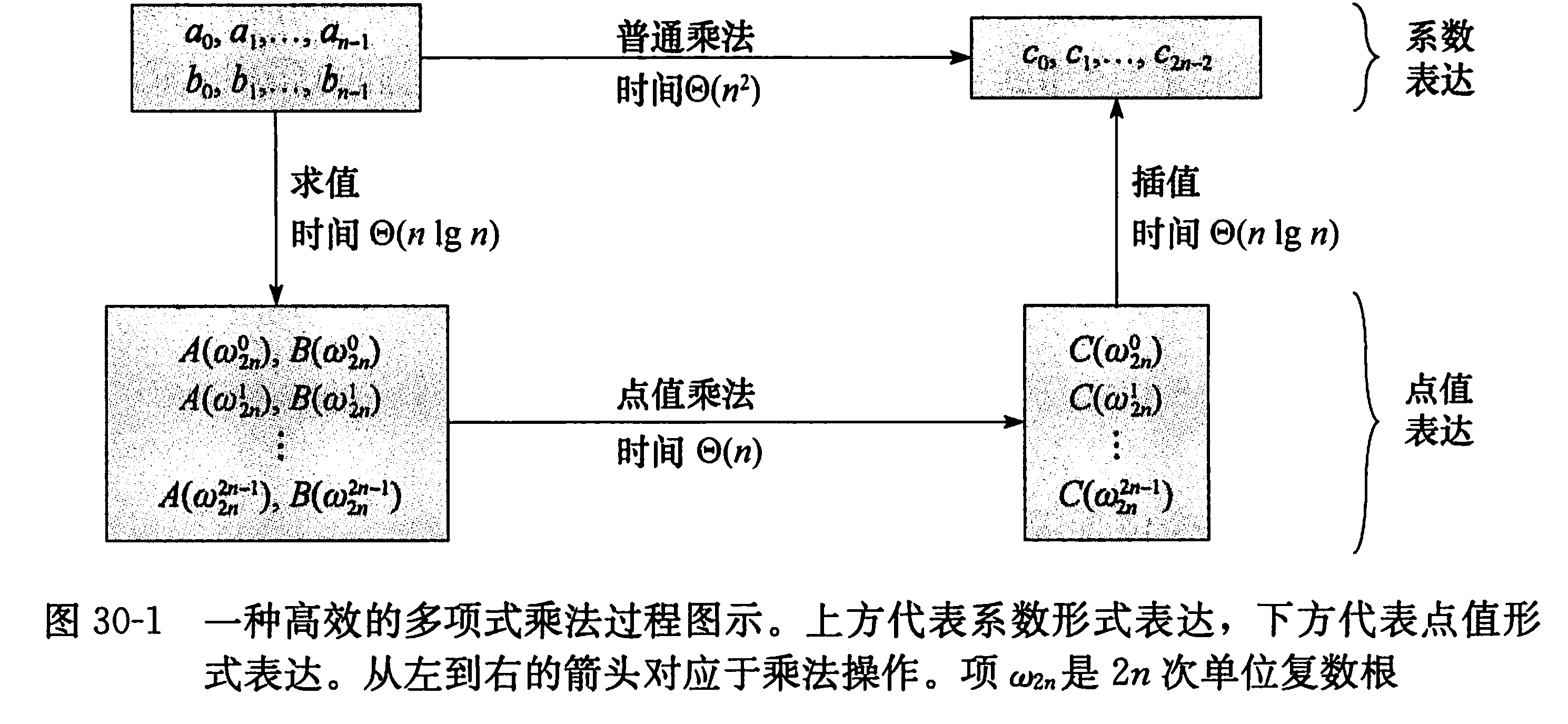
（此处先抛出，大家不用纠结，以后我还会说）FFT的灵魂在于，

它利用单位复数根的性质将多项式的系数表达和点值表达快速互化，利用点值乘法的特点快速进行乘法运算，最终高效实现了多项式乘法。

（题外话：它将一维（向量）的问题升为二维（矩阵），再降回一维（启发：我们要想得到更好的方法，必须要有更高层的技术））

 

复数：

在介绍复数之前，首先介绍一些可能会用到的东西

向量

同时具有大小和方向的量

在几何中通常用带有箭头的线段表示

圆的弧度制

等于半径长的圆弧所对的圆心角叫做1弧度的角，用符号rad表示，读作弧度。用弧度作单位来度量角的制度叫做弧度制

公式:

$1^{\circ }=\frac{\pi}{180^{\circ}}rad$

$180^{\circ }=\pi rad$

平行四边形定则

 

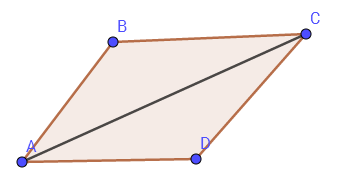
平行四边形定则：$AB+AD=AC$

复数

定义

$a$ , $b$为实数，$i^2=-1$，形如$a+bi$的数叫负数，其中$i$被称为虚数单位，复数域是目前已知最大的域

在复平面中，$x$代表实数，$y$ 轴（除原点外的点）代表虚数，从原点 $(0,0)$ 到 $(a,b)$ 的向量表示复数 $a+bi$

模长：从原点$(0,0)$到点$(a,b)$的距离，即$\sqrt{a^2+b^2}$​

幅角：假设以逆时针为正方向，从$x$轴正半轴到已知向量的转角的有向角叫做幅角

运算法则

加法：

因为在复平面中，复数可以被表示为向量，因此复数的加法与向量的加法相同，都满足平行四边形定则（就是上面那个）

乘法：

几何定义：

　　复数相乘，模长相乘，幅角相加

代数定义：

$(a+bi)*(c+di)$

$=ac+adi+bci+bdi^2$

$=ac+adi+bci-bd$

$=(ac-bd)+(bc+ad)i$

代码实现：

struct COM{/*Complex*/
    double real,imag;
    COM(){
        real=0;
        imag=0;
    }
    inline COM(double x,double y){
        real=x;
        imag=y;
    }
    friend inline COM operator + (COM x,COM y){
        return COM(x.real+y.real,x.imag+y.imag);
    }
    friend inline COM operator - (COM x,COM y){
        return COM(x.real-y.real,x.imag-y.imag);
    }
    friend inline COM operator * (COM x,COM y){
        return COM(x.real*y.real-x.imag*y.imag,x.real*y.imag+x.imag*y.real);
    }
    inline void output(){
        printf("(%lf,%lf)",real,imag);
    }
};

 

单位复数根： 

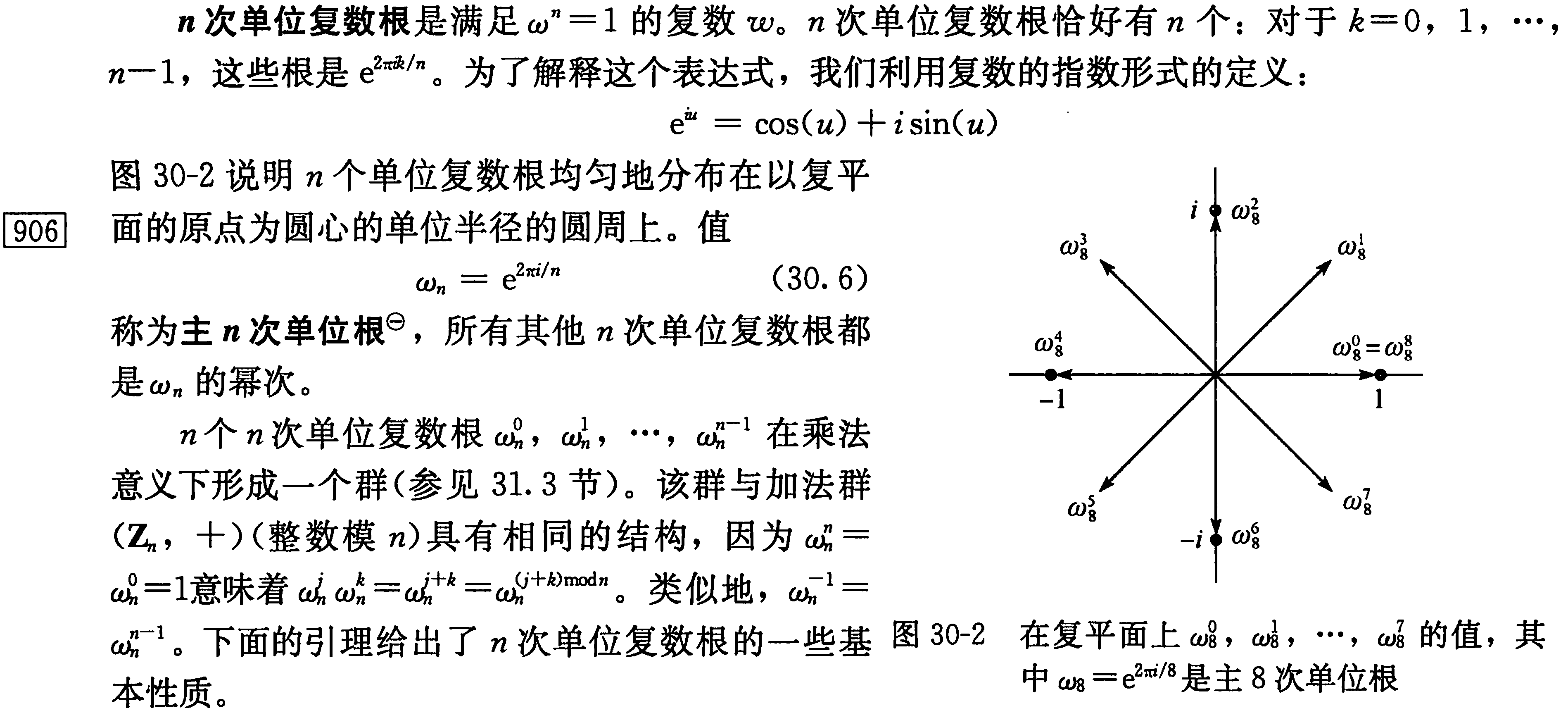
单位复数根是FFT的关键，FFT的关键就是运用单位根的性质加速运算

单位复数根的求法：

因为单位复数根均匀分布在单位圆上，所以可以根据定义直接用三角函数求解:

$∵e^{ui}=\cos(u)+i\sin(u) , w_n=e^{2{\pi}i/n}$

$∴w_n=\cos(u)+i\sin(u)$

求$w^x_{y}$代码

inline COM unit(int x,int y){
    double ii=2.0*Pi*x/y;
    return COM(cos(ii),sin(ii));
}

 

 

单位复数根的性质

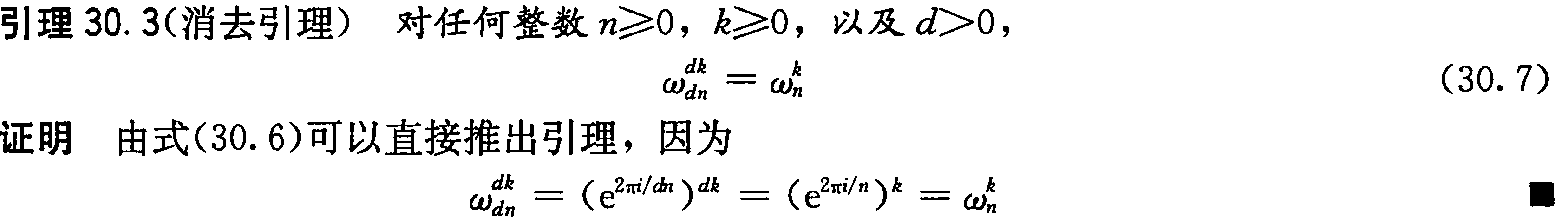
证明：

根据消去引理：

$\omega^{\frac{n}{2}}_{n}=\omega^{\frac{n}{2}*\frac{2}{n}}_{n*\frac{2}{n}}=\omega_{2}$

根据单位复数根的定义：

$\omega^{n}_{2n}=-1$

∴推论30.4显然成立

式A.5为几何级数（小奥错次相减）：

 

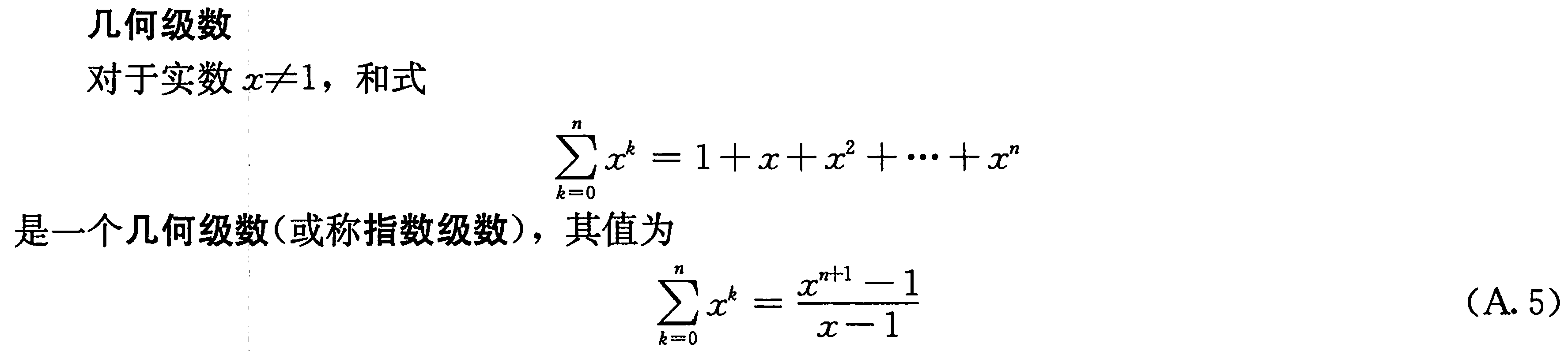
终于开始讲核心内容了：

DFT

 

FFT

此处先给出递归FFT的伪代码，随后证明其正确性：

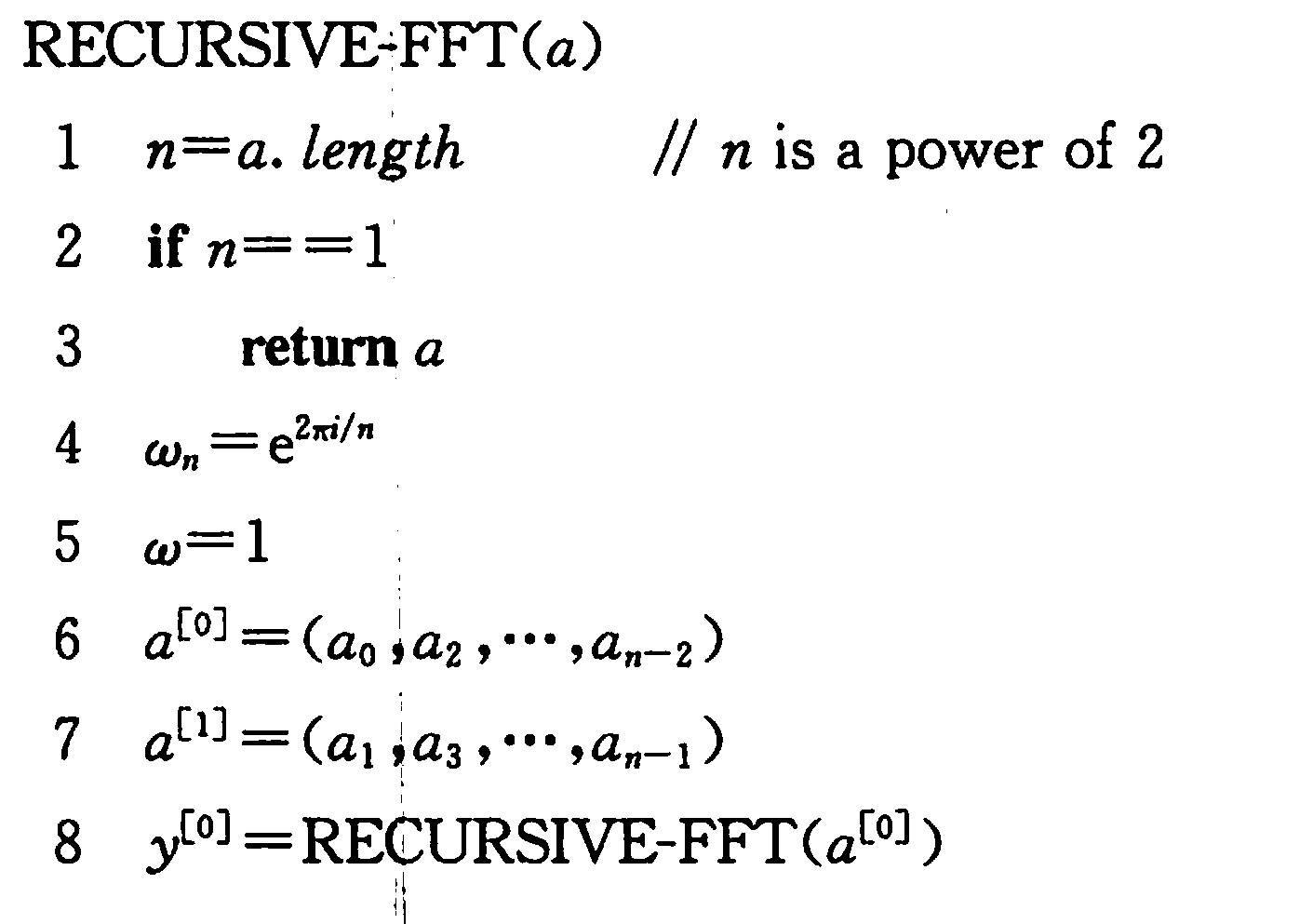
前面部分是分治，for循环中是核心代码，以下是数学证明

 

插值（从点值到系数）

（此处用了数学中的常用思想（设而不求），定义范德蒙德矩阵但不求解，利用其性质得出等式，帮助解题）

实现

递归实现

 这样，我们就基本了解了FFT的思想，此时递归实现就很简单了（可以参考上文中给出的伪代码）：

AC记录

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int INF=1e9+7,MAXN=2e6+50;
const double Pi=3.141592653589793238462;
struct COM{
    double real,imag;
    COM(){
        real=0;
        imag=0;
    }
    inline COM(double x,double y){
        real=x;
        imag=y;
    }
    friend inline COM operator + (COM x,COM y){
        return COM(x.real+y.real,x.imag+y.imag);
    }
    friend inline COM operator - (COM x,COM y){
        return COM(x.real-y.real,x.imag-y.imag);
    }
    friend inline COM operator * (COM x,COM y){
        return COM(x.real*y.real-x.imag*y.imag,x.real*y.imag+x.imag*y.real);
    }
};
void FFT(int lim,COM *a,int opt){
    if(lim==1)
        return;
    COM a0[lim>>1],a1[lim>>1];
    for(int i=0;i<lim;i+=2){
        a0[i>>1]=a[i];
        a1[i>>1]=a[i+1];
    }
    FFT(lim>>1,a0,opt);
    FFT(lim>>1,a1,opt);
    COM unit=COM(cos(2.0*Pi/lim),opt*(sin(2.0*Pi/lim))),w=COM(1,0);
    for(int i=0;i<(lim>>1);i++){
        a[i]=a0[i]+w*a1[i];
        a[i+lim/2]=a0[i]-w*a1[i];
        w=w*unit;
    }
}
int N,M;
COM a[MAXN],b[MAXN],c[MAXN];
int limit=1;
int main(){
    scanf("%d%d",&N,&M);
    for(int i=0;i<=N;i++)
        scanf("%lf",&a[i].real);
    for(int i=0;i<=M;i++)
        scanf("%lf",&b[i].real);
    while(limit<=N+M){
        limit<<=1;
    }
    FFT(limit,a,1);
    FFT(limit,b,1);
    for(int i=0;i<=limit;i++){
        c[i]=a[i]*b[i];
    }
    FFT(limit,c,-1);
    for(int i=0;i<=N+M;i++){
        printf("%d ",(int)(c[i].real/limit+0.5));
    }
    return 0;
}

但遗憾的是，这个代码并不适合实际问题，虽然时间复杂度是$\Theta(N*logN)$,空间复杂度是$\Theta(N)$(常数很大)，但因为在递归中声明数组，显然会爆栈。

如果要全局分配内存，代码就会很复杂，再次不介绍

于是，我们就需要非递归的做法。

迭代实现

递归实现之所以不优，有两方面原因（空间，时间）

空间上，如果要简单递归实现，对栈的要求非常高

时间上又有两方面，一是递归本身的效率低下，二是复数的运算非常慢，故我们要选择迭代，以合并一些复数运算

蝴蝶操作

观察之前的伪代码

其中$\omega y^1_k$出现了两次，则该值为公用子表达式，可以用临时变量优化成

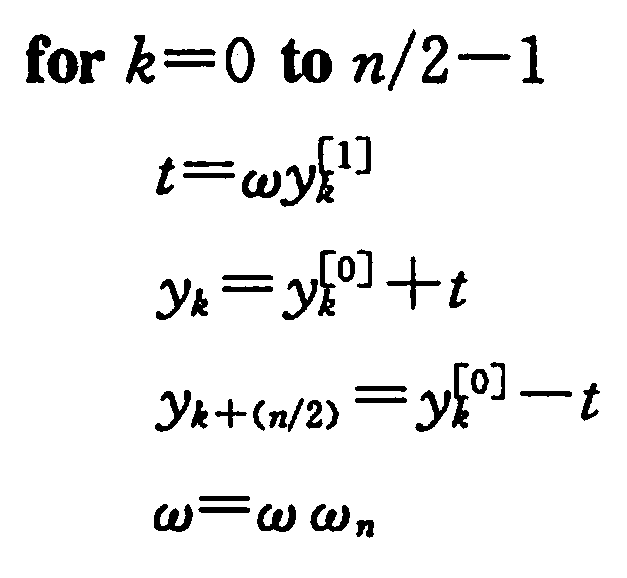
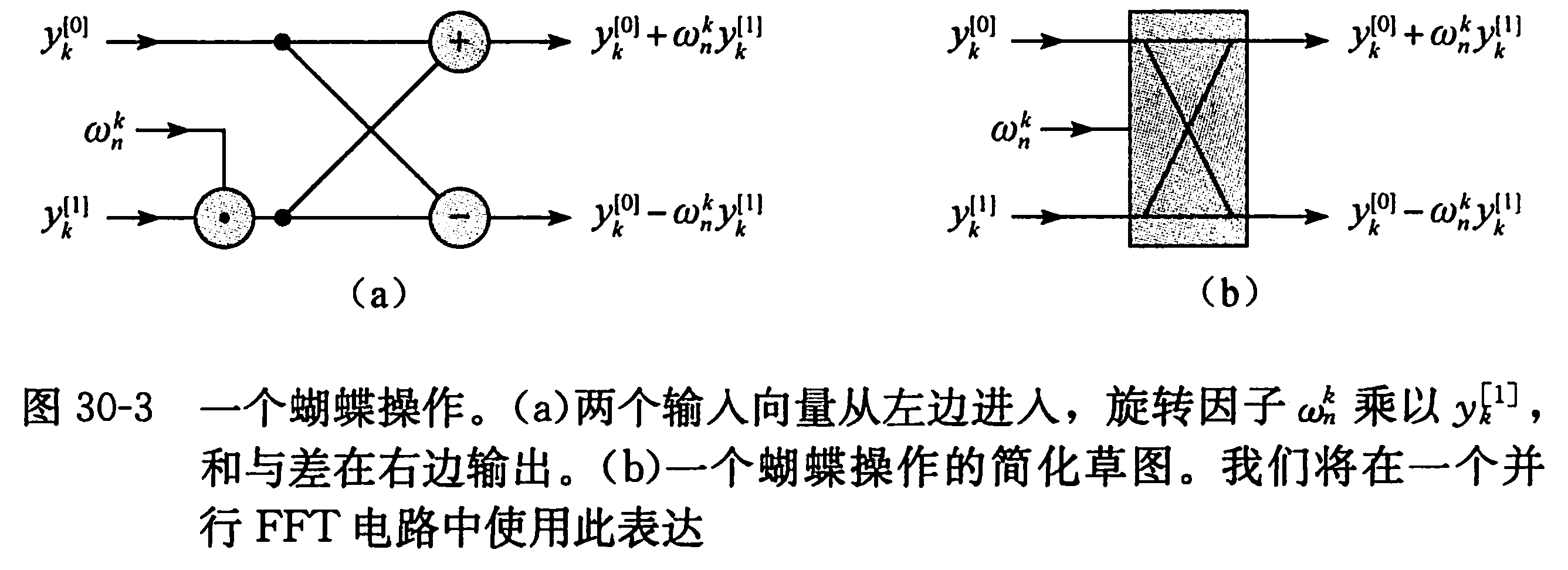
光是这样，只能很小程度地优化，但如果我们将递归转成递推，同一个$\omega$的值就可以用于多次蝴蝶操作

 

递归转递推

刚才讲到“如果能将递归转成递推”，但这转化并不像普通分治那么简单，因为我们在$FFT$中是按照奇偶分治的，所以要先对递推数组进行处理

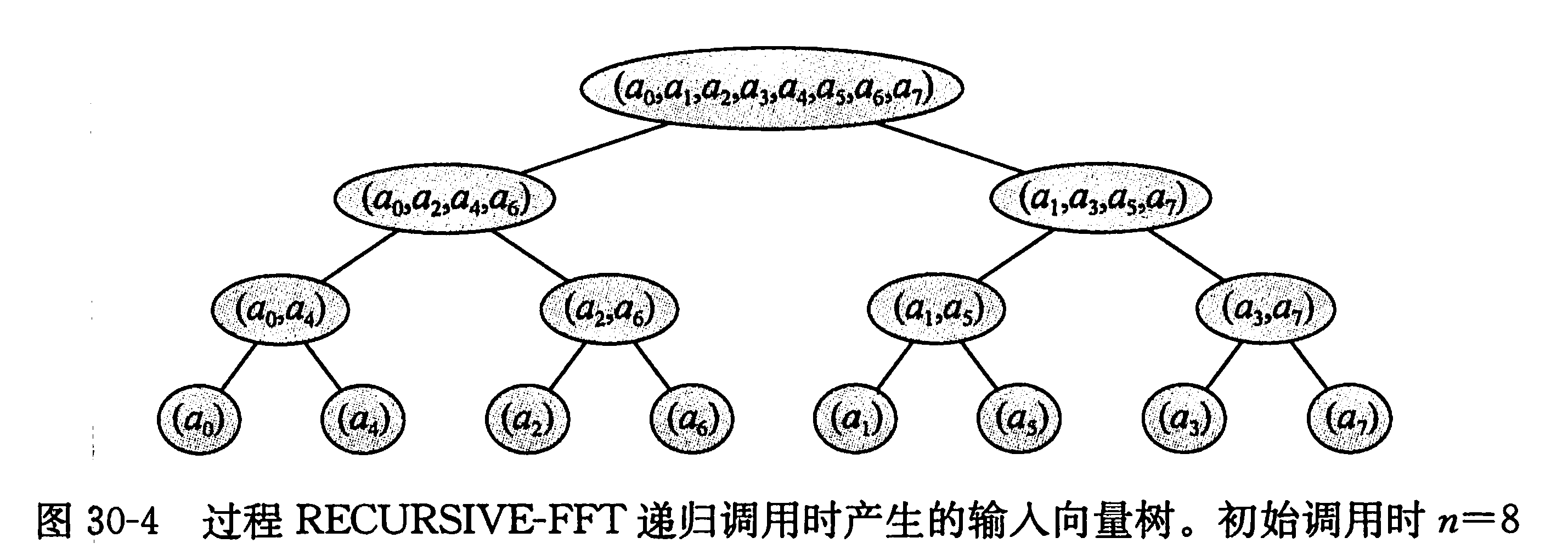
如图，我们要将初始数组从${a_0,a_1,a_2,a_3,a_4,a_5,a_6,a_7}$转成${a_0,a_4,a_2,a_6,a_1,a_5,a_3,a_7}$

显然，我们可以在$\Theta(NlogN)$内完成，但这样做显然增大了常数，我们需要$\Theta(N)$的做法

此处先给出做法：

1. 先预处理出一个存储每个数二进制翻转后的数组$rev$（例如$[0,2^3)$中$001$变成$100$）

for(int i=0;i<limit;i++)
    r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));

 

1. 然后对于原数组$A$，如果下标小于$rev$中的值($i<rev_i$)则交换$A_i,A_{rev_i}$

for(int i=0;i<limit;i++) 
    if(i<r[i])
        swap(A[i],A[r[i]]);

 

效果：

$rev$数组：
$000\rightarrow000$
$001\rightarrow100$
$010\rightarrow010$
$011\rightarrow110$
$100\rightarrow001$
$101\rightarrow101$
$110\rightarrow011$
$111\rightarrow111$

过程
$ 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 \leftarrow {000\rightarrow000}$
$ 0 , 4 , 2 , 3 , 1 , 5 , 6 , 7 \leftarrow {001\rightarrow100}$
$ 0 , 4 , 2 , 3 , 1 , 5 , 6 , 7 \leftarrow {010\rightarrow010}$
$ 0 , 4 , 2 , 6 , 1 , 5 , 3 , 7 \leftarrow {011\rightarrow110}$
$ 0 , 4 , 2 , 6 , 1 , 5 , 3 , 7 \leftarrow {100\rightarrow001}$
$ 0 , 4 , 2 , 6 , 1 , 5 , 3 , 7 \leftarrow {101\rightarrow101}$
$ 0 , 4 , 2 , 6 , 1 , 5 , 3 , 7 \leftarrow {110\rightarrow011}$
$ 0 , 4 , 2 , 6 , 1 , 5 , 3 , 7 \leftarrow {111\rightarrow111}$

证明：

FFT的递归树就是按照二进制反序分配的，即每个数的位置就是它的原下标的二进制反序。故预处理出二进制反序，每次当前下标小于rev数组则交换（防止重复交换）

 

至于代码实现，就很简单了：

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int INF=1e9+7,MAXN=4e6+50;
const double Pi=3.141592653589793238462;
struct COM{
    double real,imag;
    COM(){ real=0;imag=0; }
    inline COM(double x,double y){ real=x;imag=y; }
    friend inline COM operator + (COM x,COM y){ return COM(x.real+y.real,x.imag+y.imag); }
    friend inline COM operator - (COM x,COM y){ return COM(x.real-y.real,x.imag-y.imag); }
    friend inline COM operator * (COM x,COM y){ return COM(x.real*y.real-x.imag*y.imag,x.real*y.imag+x.imag*y.real); }
    inline void output(){ printf("(%lf,%lf)",real,imag); }
};
int rev[MAXN];
void FFT(int lim,COM *a,int opt){
    int lg=log2(lim);
    for(int i=0;i<lim;i++)
        if(i<rev[i])
            swap(a[i],a[rev[i]]);
    for(int i=0;i<=lg;i++){
        int len=1<<i;
        COM unit=COM(cos(2.0*Pi/len),sin(opt*2.0*Pi/len));
        for(int j=0;j<lim;j+=len){
            COM w=COM(1,0);
            for(int k=0;k<(len>>1);k++){
                COM t1=a[j+k],t2=w*a[j+k+(len>>1)];
                a[j+k]=t1+t2;
                a[j+k+(len>>1)]=t1-t2;
                w=w*unit;
            }
        }
    }
}
int N,M;
COM a[MAXN],b[MAXN],c[MAXN];
int limit=1,lgn;
int main(){
    scanf("%d%d",&N,&M);
    for(int i=0;i<=N;i++)
        scanf("%lf",&a[i].real);
    for(int i=0;i<=M;i++)
        scanf("%lf",&b[i].real);
    while(limit<=N+M){
        limit<<=1;
        lgn++;
    }
    for(int i=0;i<limit;i++)
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(lgn-1));
    FFT(limit,a,1);
    FFT(limit,b,1);
    for(int i=0;i<limit;i++){
        c[i]=a[i]*b[i];
    }
    FFT(limit,c,-1);
    for(int i=0;i<=N+M;i++){
        printf("%d ",(int)(c[i].real/limit+0.5));
    }
    return 0;
}