图
1.学习总结(2分)
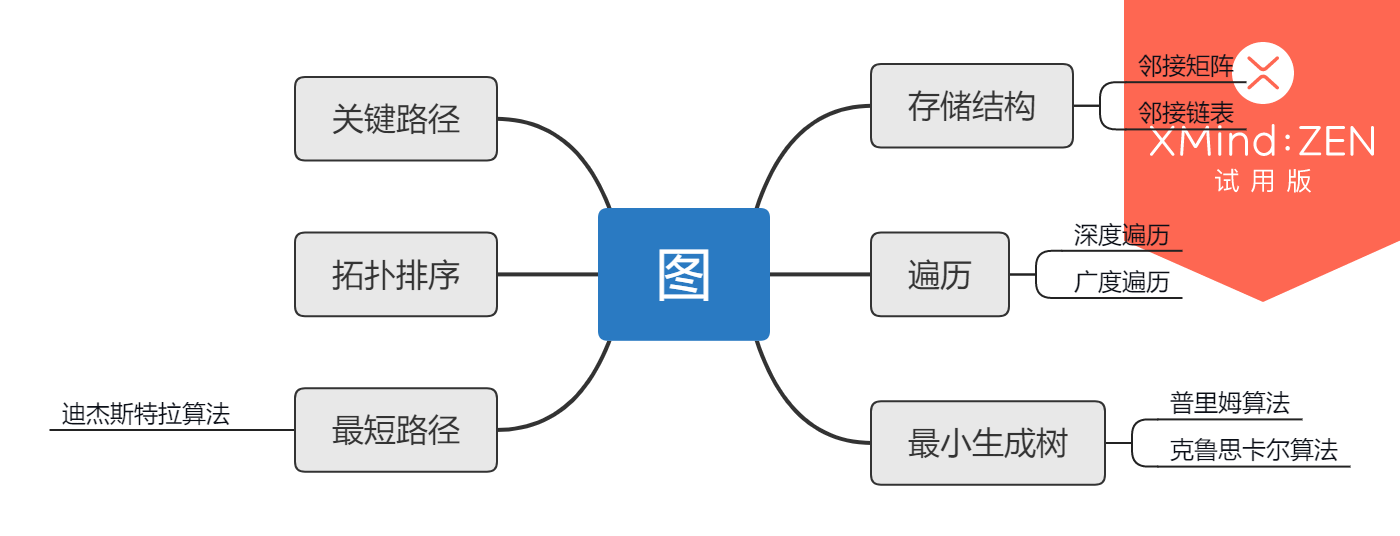
1.1图的思维导图
图的存储结构--图的遍历---最小生成树--最短路径---拓扑排序、关键路径,这些知识点需要都梳理。
1.2 图结构学习体会
谈谈你对图结构中的几个经典算法学习体会。具体有:
深度遍历算法
遍历邻接点的邻接点
可用于图着色算法
广度遍历算法
遍历一个顶点的所有邻接点
可用于六度空间算法
Prim和Kruscal算法
用于最小生成树
可用于公路村村通
Dijkstra算法
用于寻找最短路径
拓扑排序算法
选择没有前驱的结点并输出,只适用于AOV图
可用于判断是否是有向无环图
2.PTA实验作业(4分)
2.1 题目1:7-1 图着色问题
2.2 设计思路(伪代码或流程图)
int visited[1000]
int flag=0
main函数
创建邻接矩阵
输入图的顶点个数n,边数e,颜色数k和着色次数t
for p=1 to p<=t
count1=0;count2=0;flag=0 fl=0
for i=0 to i<=n
依次输入图的颜色并计算颜色的种类
end for
如果输入的颜色种类不等于k则输出No
else
for y=1 to y<=n visited[y]=0
DFS(G,1)
end for
if flag==1 输出No
else
for y=1 to y<=n
if visited[y]==0 DFS(G,y)
end for
if flag==1 输出No
else 输出Yes
end for
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
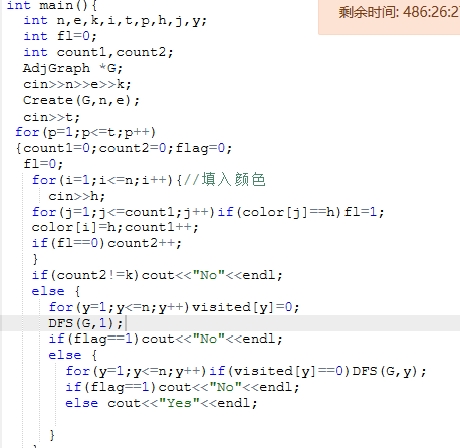
2.4 PTA提交列表说明。
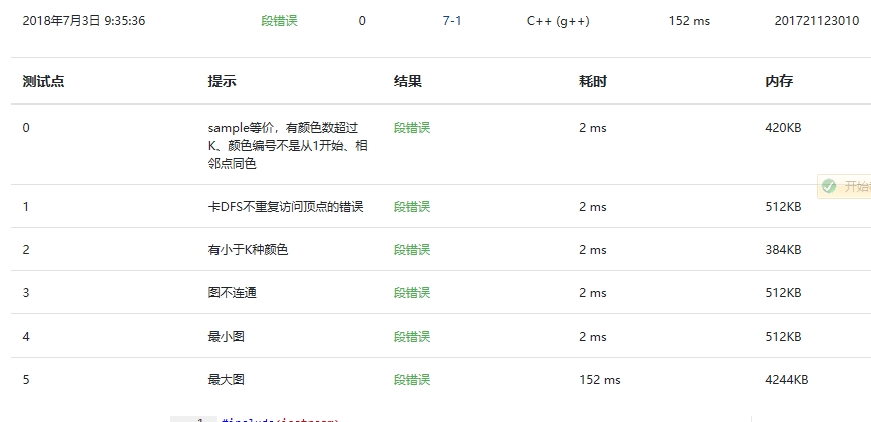
调试了N多遍,好多天,也很仔细地从头到尾检查了,觉得大致思路都没问题,但就是段错误,有点崩溃,会继续调试。。。。。。
2.1 题目1:7-3 六度空间
2.2 设计思路(伪代码或流程图)
int visited[1000]
void Sixdegree(graph g,int v)
cnt表示朋友数,degree表示层数,last记录该层最后一个结点
建立队列q1
visited[v]=1;
v 入队列
while 队列不为空且degree<=6
v1=队首元素
队首元素出队列
for i=1 to i<=g.n
if i结点未被访问且v1和i之间有通路{
visited[i]=1,结点i入队列
cnt自增;}
end for
if v1==last
degree自增
last等于队尾元素
end while
输出结果
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
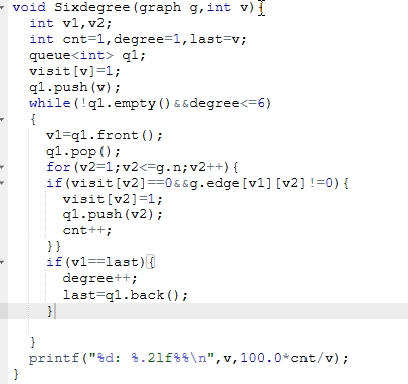
2.4 PTA提交列表说明。

这题也是调了很久还是段错误,可是检查了很多遍也没看出什么问题,感觉应该是和7-1一样的问题,就是运行不了,一开始 以为可能是我建图函数出问题,可是仔细看了几遍也没问题,然后又看六度空间函数,也没找出什么问题,真的邪了门了,会继续调试。。。。。。终于调试出来了,我参考了同学的建议把邻接矩阵直接改成二维数组来做就没有段错误的问题了,但是答案错误,仔细找了下发现自己将其当成有向图来写,创建二维数组时只让edge[k][x]=1而没让edge[x][k]=1,导致后面的顶点到前面没有通路,如下:
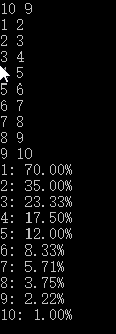
后来改了一下就正确了,如下:

然后答案就对了
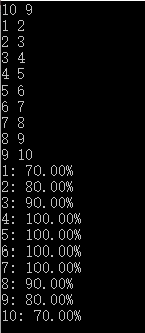
提交列表如下:
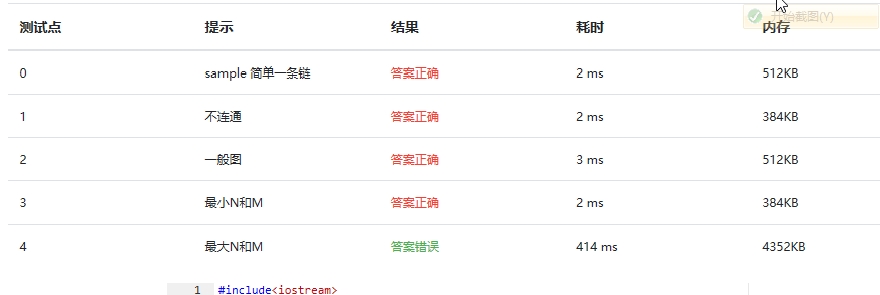
2.1 题目1:7-4 公路村村通
2.2 设计思路(伪代码或流程图)
int Prim(int G[MAXV][MAXV],int v)//prim算法计算最短路径
{
定义数组 lowcost[MAXV],closest[MAXV];
lowcost[1]=0;
closest[1]=0;
for i=2 to 顶点数 {
lowcost[i]=G[v][i];
closest[i]=v;
}
for i=2 to 顶点数 {
min置为INFINITY
for j=2 to 顶点数 {
在(V-U)中找出离U最近的顶点k
k记录最近顶点的编号
}
以last更新记录权值长度
lowcost[k]=0;
for j=2 to 顶点数{
若 顶点未被访图联通{
更新
k记录最近顶点
}
}
}
返回last的值
}
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)

2.4 PTA提交列表说明。
这题还是有段错误,会继续调试
3.截图本周题目集的PTA最后排名(3分)
本次题目集总分:310分
3.1 PTA排名(截图带自己名字的排名)
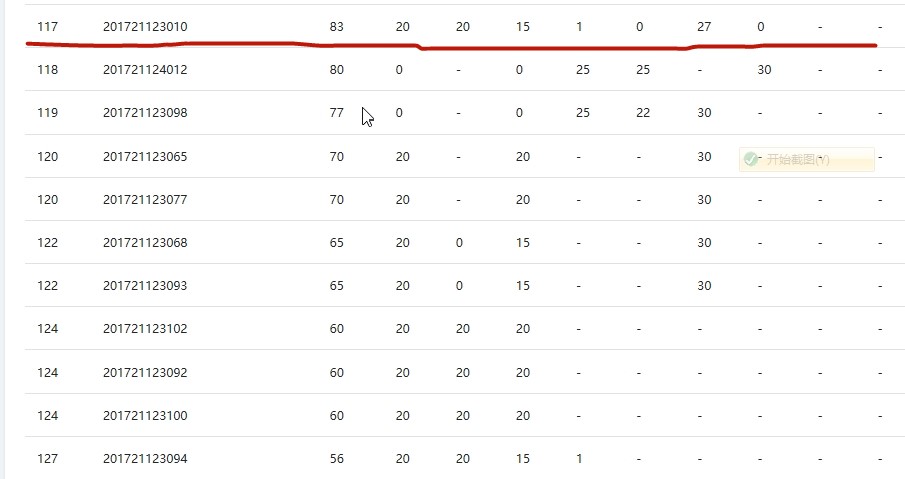
3.2 我的总分:83分
- 阅读代码(必做,1分)

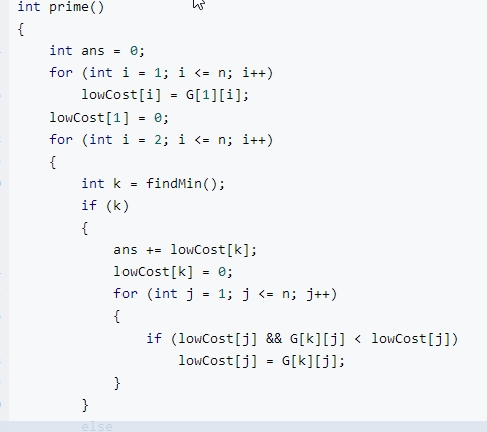


用的是最小生成树 的方法 ,然后 自己写的最小生成树 的思路 超时了,就是 对每一个 已经入队的 点 一个一个遍历 寻找下一个最短路径,但是 更好的方法是 ,对每一个点 入队 ,更新 到 未入队的点的最短距离 就是 距离比原先的距离小 就更新 这样每次对每个点 更新 那么就能保证 lowCost 中的 距离 在当前状态下就是最小的,然后每次 让 距离最短的 入队 就可以了。



