oj算法----动态规划----背包问题

oj算法----动态规划----背包问题

1.动态规划

1.1概念

动态规划(dynamic programming)是运筹学的一个分支，是求解决策过程(decision process)最优化的数学方法

1.2性质

动态规划一般用来处理最优解的问题。使用动态规划算法思想解决的问题一般具有最优子结构性质和重叠子问题这两个因素。

<1> 最优子结构

     一个问题的最优解包含其子问题的最优解，这个性质被称为最优子结构性质 

<2> 重叠子问题

     递归算法求解问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次。这种性质称为子问题的重叠性质。

1.3与分治法的区别

动态规划和分治法有相似之处，都是将待解决问题分解为若干子问题。不同之处，分治法求解时有些子问题被重复计算了许多次；动态规划实现了存储这些子问题的解，以备子问题重复出现，当重叠子问题出现，找到已解决子问题的解即可，避免了大量的重复计算。

1.4在优化

可以考虑在空间上进行优化，例如背包问题，将二维数组优化成两个一维数组，进而再优化成一个一维数组

2.背包问题

2.1背包问题又分成0/1背包问题，完全背包问题，以及多重背包问题（本质区别就是到底max多少种情况）

2.2 01背包问题

递推关系式

① j<w(i)      V(i,j)=V(i-1,j) 

② j>=w(i)     V(i,j)=max｛ V(i-1,j)，V(i-1,j-w(i))+v(i) ｝

 图解

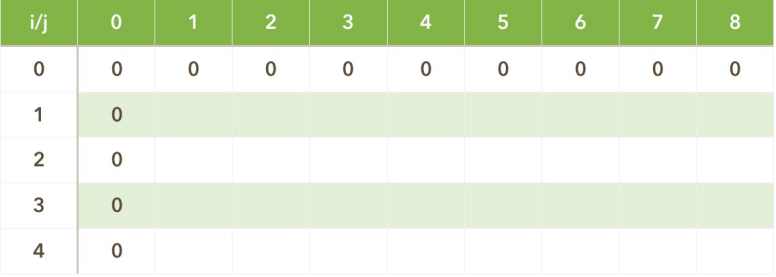
一定要注意初始化的问题

 

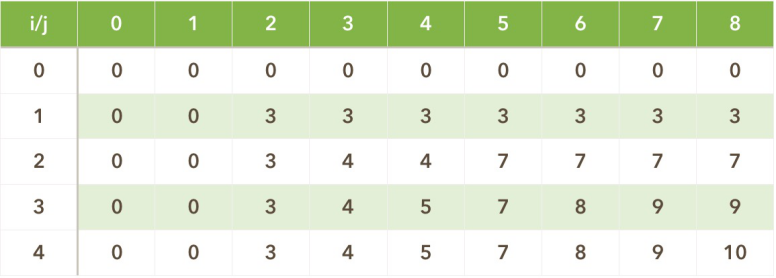
 空间优化

由上面的图可以看出来，每一次V(i)(j)改变的值只与V(i-1)(x) {x:1...j}有关，V(i-1)(x)是前一次i循环保存下来的值；

因此，可以将V缩减成一维数组，从而达到优化空间的目的，状态转移方程转换为 B(j)= max{B(j), B(j-w(i))+v(i)}；

并且，状态转移方程，每一次推导V(i)(j)是通过V(i-1)(j-w(i))来推导的，所以一维数组中j的扫描顺序应该从大到小(capacity到0)，否者前一次循环保存下来的值将会被修改，从而造成错误。

#include <stdio.h>
#include <string.h>
 
int f[1010],w[1010],v[1010];//f记录不同承重量背包的总价值，w记录不同物品的重量，v记录不同物品的价值
 
int max(int x,int y){//返回x,y的最大值
    if(x>y) return x;
    return y;
}
 
int main(){
    int t,m,i,j;
    memset(f,0,sizeof(f));  //总价值初始化为0
    scanf("%d %d",&t,&m);  //输入背包承重量t、物品的数目m
    for(i=1;i<=m;i++)
        scanf("%d %d",&w[i],&v[i]);  //输入m组物品的重量w[i]和价值v[i]
    for(i=1;i<=m;i++){  //尝试放置每一个物品
        for(j=t;j>=w[i];j--){//倒叙是为了保证每个物品都使用一次
            f[j]=max(f[j-w[i]]+v[i],f[j]);
            //在放入第i个物品前后，检验不同j承重量背包的总价值，如果放入第i个物品后比放入前的价值提高了，则修改j承重量背包的价值，否则不变
        }
    }
    printf("%d",f[t]);  //输出承重量为t的背包的总价值
    printf("\n");
    getch();
    return 0;
} 

2.3完全背包

每种物品的数量不限制

2.3.1 简单方法

根据第i种物品放多少件进行决策，所以状态转移方程为

   

与01背包相同，完全背包也需要求出NV个状态F[i][j]。但是完全背包求F[i][j]时需要对k分别取0,…，j/C[i]求最大F[i][j]值。（实际上就是更新每个状态的时候不再是max两种情况，放入一个或者放入0个，而是maxK种情况，放入0个，1个，2个，3个......直到k个）

这样代码应该是三层循环（物品数量，物品种类，背包大小这三个循环）

F[0][] ← {0}  
  
F[][0] ← {0}  
  
for i←1 to N  
  
    do for j←1 to V  
  
        do for k←0 to j/C[i]  
  
           if(j >= k*C[i])  
  
                then F[i][k] ← max(F[i][k],F[i-1][j-k*C[i]]+k*W[i])  
  
return F[N][V]

这样是三层循环，所以考虑优化

2.3.2 优化方法

 

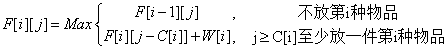
这里注意，当j>=C[i]时候，是对照F[i][j-C[j]]更新，而不是F[i-1][j-C[j]]。因为F[i][j-C[j]]状态本身包含了max了k-1种情况（他max了放入0个，放入1个......放入k-1的情况），而后者只max了一种情况，就是放入0个的情况！！！

2.3.3 0-1背包和完全背包的不同：

从二维数组上区别0-1背包和完全背包也就是状态转移方程就差别在放第i中物品时，完全背包在选择放这个物品时，最优解是F[i][j-c[i]]+w[i]即画表格中同行的那一个，而0-1背包比较的是F[i-1][j-c[i]]+w[i]，上一行的那一个。

从一维数组上区别0-1背包和完全背包差别就在循环顺序上，0-1背包必须逆序，因为这样保证了不会重复选择已经选择的物品，而完全背包是顺序，顺序会覆盖以前的状态，所以存在选择多次的情况，也符合完全背包的题意。状态转移方程都为F[i] = max(F[i],dp[F-c[i]]+v[i])。
2.3.4 代码实现完全背包

#include<cstdio>
#include<algorithm>
using namespace std;
int w[300],c[300],f[300010];
int V,n;
int main()
{
    scanf("%d%d",&V,&n);
    for(int i=1; i<=n; i++)
    {
        scanf("%d%d",&w[i],&c[i]);
    }
    for(int i=1; i<=n; i++)
        for(int j=w[i]; j<=V; j++)//注意此处，与0-1背包不同，这里为顺序，0-1背包为逆序
            f[j]=max(f[j],f[j-w[i]]+c[i]);
    printf("max=%d\n",f[V]);
    return 0;
}

2.4 多重背包

2.4.1 简单方法

就是max有限个m种情况

2.4.2 优化方法

转化为01背包求解：把第i种物品换成n[i]件01背包中的物品。考虑二进制的思想，考虑把第i种物品换成若干件物品，使得原问题中第i种物品可取的每种策略——取0..n[i]件——均能等价于取若干件代换以后的物品。另外，取超过n[i]件的策略必不能出现。

方法是：将第i种物品分成若干件物品，其中每件物品有一个系数，这件物品的费用和价值均是原来的费用和价值乘以这个系数。使这些系数分别为1,2,4,...,2^(k-1),n[i]-2^k+1，且k是满足n[i]-2^k+1>0的最大整数。例如，如果n[i]为13，就将这种物品分成系数分别为1,2,4,6的四件物品。

分成的这几件物品的系数和为n[i]，表明不可能取多于n[i]件的第i种物品。另外这种方法也能保证对于0..n[i]间的每一个整数，均可以用若干个系数的和表示，证明我也没看过这里就不贴上了，主要还是需要去理解代码，代码在下面给出。
2.4.3 代码实现

#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <cstring>
#define MAX 1000000
using namespace std;
 
int dp[MAX];//存储最后背包最大能存多少
int value[MAX],weight[MAX],number[MAX];//分别存的是物品的价值，每一个的重量以及数量
int bag;
 
void ZeroOnePack(int weight,int value )//01背包
{
    int i;
    for(i = bag; i>=weight; i--)
    {
        dp[i] = max(dp[i],dp[i-weight]+value);
    }
}
void CompletePack(int weight,int value)//完全背包
{
    int i;
    for(i = weight; i<=bag; i++)
    {
        dp[i] = max(dp[i],dp[i-weight]+value);
    }
}
void MultiplePack(int weight,int value,int number)//多重背包
{
    if(bag<=number*weight)//如果总容量比这个物品的容量要小，那么这个物品可以直到取完，相当于完全背包
    {
        CompletePack(weight,value);
        return ;
    }
    else//否则就将多重背包转化为01背包
    {
        int k = 1;
        while(k<=number)
        {
            ZeroOnePack(k*weight,k*value);
            number = number-k;
            k = 2*k;//这里采用二进制思想
        }
        ZeroOnePack(number*weight,number*value);
    }
}

int main()
{
    int n;
    while(~scanf("%d%d",&bag,&n))
    {
        int i,sum=0;
        for(i = 0; i<n; i++)
        {
            scanf("%d",&number[i]);//输入数量
            scanf("%d",&value[i]);//输入价值  此题没有物品的重量，可以理解为体积和价值相等
        }
        memset(dp,0,sizeof(dp));
        for(i = 0; i<n; i++)
        {
            MultiplePack(value[i],value[i],number[i]);//调用多重背包,注意穿参的时候分别是重量，价值和数量
        }
        cout<<dp[bag]<<endl;
    }
    return 0;
}
 

其他

参考链接

https://blog.csdn.net/niaonao/article/details/78249256

https://blog.csdn.net/qq_38984851/article/details/81133840

https://www.cnblogs.com/aiguona/p/7274222.html

拓展

1.硬币问题本质和背包问题一样，只不过有一种无解的状态

2.学习二进制压缩的思想，其思想十分的优雅和先进