OTSU算法学习 OTSU公式证明
OTSU算法学习 OTSU公式证明
1 otsu的公式如下,如果当前阈值为t,
w0 前景点所占比例
w1 = 1- w0 背景点所占比例
u0 = 前景灰度均值
u1 = 背景灰度均值
u = w0*u0 + w1*u1 全局灰度均值
g = w0(u0-u)*(u0-u) + w1(u1-u)*(u1-u) = w0*(1 – w0)*(u0 - u1)* (u0 - u1)
目标函数为g, g越大,t就是越好的阈值.为什么采用这个函数作为判别依据,直观是这个函数反映了前景和背景的差值.
差值越大,阈值越好.
下面是一段证明g的推导的matlab代码
|
syms w0 u0 u1 %w0 前景均值 u0 前景灰度均值 u1 背景灰度均值 %背景均值 w1 =1- w0; %全局灰度均值 u=w0*u0+w1*u1; %目标函数 g=w0*(u0-u)*(u0-u)+w1*(u1-u)*(u1-u); %化简的形式 g1 =w0*w1*(u0-u1)*(u0-u1); %因式展开 a1 = expand(g)%结果是 - u0^2*w0^2 + u0^2*w0 + 2*u0*u1*w0^2 - 2*u0*u1*w0 - u1^2*w0^2 + u1^2*w0 a2 = expand(g)%结果是 - u0^2*w0^2 + u0^2*w0 + 2*u0*u1*w0^2 - 2*u0*u1*w0 - u1^2*w0^2 + u1^2*w0 %对g进行因式分解 a2 = factor(g)%结果 -w0*(u0 - u1)^2*(w0 - 1) |
这里是matlab初等代数运算的讲解 http://wenku.baidu.com/link?url=SODqdtPjbNLhKPEvCjsHkOhMi9LMb34qIrnp9_QRBKUNqPLGLxRCuLJgL2sp1vhLk55b6hpp242-RTCVp6ma_7a7-0imT3WVyBcsTmQ-5HS
2 关于最大类间方差法(otsu)的性能:
类间方差法对噪音和目标大小十分敏感,它仅对类间方差为单峰的图像产生较好的分割效果。
当目标与背景的大小比例悬殊时,类间方差准则函数可能呈现双峰或多峰,此时效果不好,但是类间方差法是用时最少的。
3 代码实现
|
public int GetThreshValue(Bitmap image) { BitmapData bd = image.LockBits(new Rectangle(0,0, image.Width, image.Height), ImageLockMode.WriteOnly, image.PixelFormat); byte* pt =(byte*)bd.Scan0; int[] pixelNum = new int[256];//图象直方图,共256个点 byte color; byte* pline; int n, n1, n2; int total;//total为总和,累计值 double m1, m2, sum, csum, fmax, sb;//sb为类间方差,fmax存储最大方差值 int k, t, q; int threshValue =1;// 阈值 int step =1; switch(image.PixelFormat) { case PixelFormat.Format24bppRgb: step =3; break; case PixelFormat.Format32bppArgb: step =4; break; case PixelFormat.Format8bppIndexed: step =1; break; } //生成直方图 for(int i =0; i < image.Height; i++) { pline = pt + i * bd.Stride; for(int j =0; j < image.Width; j++) { color =*(pline + j * step);//返回各个点的颜色,以RGB表示 pixelNum[color]++;//相应的直方图加1 } } //直方图平滑化 for(k =0; k <=255; k++) { total =0; for(t =-2; t <=2; t++)//与附近2个灰度做平滑化,t值应取较小的值 { q = k + t; if(q <0)//越界处理 q =0; if(q >255) q =255; total = total + pixelNum[q];//total为总和,累计值 } //平滑化,左边2个+中间1个+右边2个灰度,共5个,所以总和除以5,后面加0.5是用修正值 pixelNum[k]=(int)((float)total /5.0+0.5); } //求阈值 sum = csum =0.0; n =0; //计算总的图象的点数和质量矩,为后面的计算做准备 for(k =0; k <=255; k++) { //x*f(x)质量矩,也就是每个灰度的值乘以其点数(归一化后为概率),sum为其总和 sum +=(double)k *(double)pixelNum[k]; n += pixelNum[k];//n为图象总的点数,归一化后就是累积概率 } fmax =-1.0;//类间方差sb不可能为负,所以fmax初始值为-1不影响计算的进行 n1 =0; for(k =0; k <255; k++)//对每个灰度(从0到255)计算一次分割后的类间方差sb { n1 += pixelNum[k];//n1为在当前阈值遍前景图象的点数 if(n1 ==0){continue;}//没有分出前景后景 n2 = n - n1;//n2为背景图象的点数 //n2为0表示全部都是后景图象,与n1=0情况类似,之后的遍历不可能使前景点数增加,所以此时可以退出循环 if(n2 ==0){break;} csum +=(double)k * pixelNum[k];//前景的“灰度的值*其点数”的总和 m1 = csum / n1;//m1为前景的平均灰度 m2 =(sum - csum)/ n2;//m2为背景的平均灰度 sb =(double)n1 *(double)n2 *(m1 - m2)*(m1 - m2);//sb为类间方差 if(sb > fmax)//如果算出的类间方差大于前一次算出的类间方差 { fmax = sb;//fmax始终为最大类间方差(otsu) threshValue = k;//取最大类间方差时对应的灰度的k就是最佳阈值 } } image.UnlockBits(bd); image.Dispose(); return threshValue; }
|
4 二维otsu算法
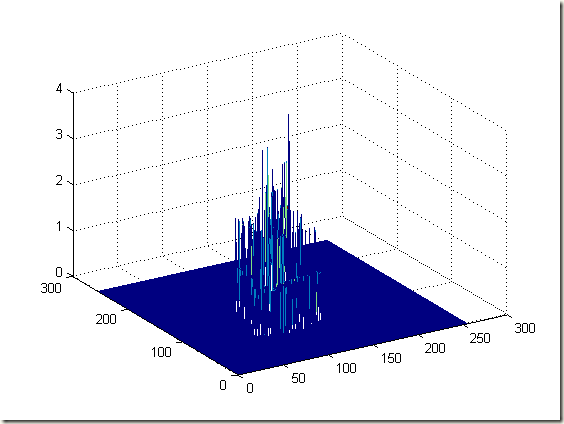
下图是二维otsu的立体图,是对右边的A进行二维直方图统计得到的图像, 遍历区域为5*5.
这是对应的matlab代码
|
%统计二维直方图 i 当前点的亮度 j n*n邻域均值亮度 function hist2 = hist2Function(image, n)
%初始化255*2565矩阵 hist2 = zeros(255,255);
[height, width]= size(image);
for i =1:height for j =1:width data = image(i,j);
tempSum =0.0; for l =-n:1:n for m =-n:1:n x = i + l; y = j+m;
if x <1 x =1; elseif x > width x = width; end
if y <1 y =1; elseif y > height y = height; end tempSum = tempSum + double(image(y,x)); end end
tempSum = tempSum /((2*n+1)*(2*n+1));
hist2(data,floor(tempSum))= hist2(data,floor(tempSum))+1; end end
%加载图像 imagea = imread('a.bmp'); %显示图像 %imshow(imagea); %显示直方图 %figure;imhist(imagea); %计算二维直方图 hist2 = hist2Function(imagea,2); %显示二维直方图 [x,y]=meshgrid(1:1:255); mesh(x,y,hist2)
|
<灰度图象的二维Otsu自动阈值分割法.pdf> 这篇文章讲解的不错.文章这里有下载http://download.csdn.net/detail/wisdomfriend/9046341
下面用数学语言表达一下
i :表示亮度的维度
j : 表示点区域均值的维度
w0: 表示在阈值(s,t)时 所占的比例
w1: 表示在阈值(s,t)时, 所占的比例
u0(u0i, u0j): 表示在阈值(s,t)时时 的均值.u0时2维的
u1(u1i, u1j): 表示在阈值(s,t)时的均值.u1时2维的
uT: 全局均值
和一维otsut函数类似的目标函数
sb = w0(u0-uT)*(u0-uT)’ + w1(u1-uT)*(u1-uT)’
= w0[(u0i-uTi)* (u0i-uTi) + (u0j-uTj)* (u0j-uTj)] + w1[(u1i-uTi)* (u1i-uTi) + (u1j-uTj)* (u1j-uTj)]
这里是代码实现.出自这篇文章:http://blog.csdn.net/yao_wust/article/details/23531031
|
int histogram[256][256]; double p_histogram[256][256]; double Pst_0[256][256];//Pst_0用来存储概率分布情况 double Xst_0[256][256];//存储x方向上的均值矢量 int OTSU2d(IplImage * src) { int height = src->height; int width = src->width; long pixel = height * width;
int i,j;
for(i =0;i <256;i++)//初始化直方图 { for(j =0; j <256;j++) histogram[i][j]=0; }
IplImage * temp = cvCreateImage(cvGetSize(src),8,1); cvSmooth(src,temp,CV_BLUR,3,0);
for(i =0;i < height;i++)//计算直方图 { for(j =0; j < width;j++) { int data1 = cvGetReal2D(src,i,j); int data2 = cvGetReal2D(temp,i,j); histogram[data1][data2]++; } }
for(i =0; i <256;i++)//直方图归一化 for(j =0; j <256;j++) p_histogram[i][j]=(histogram[i][j]*1.0)/(pixel*1.0);
Pst_0[0][0]= p_histogram[0][0]; for(i =0;i <256;i++)//计算概率分布情况 for(j =0;j <256;j++) { double temp =0.0; if(i-1>=0) temp = temp + Pst_0[i-1][j]; if(j-1>=0) temp = temp + Pst_0[i][j-1]; if(i-1>=0&& j-1>=0) temp = temp - Pst_0[i-1][j-1]; temp = temp + p_histogram[i][j]; Pst_0[i][j]= temp; }
Xst_0[0][0]=0* Pst_0[0][0]; for(i =0; i <256;i++)//计算x方向上的均值矢量 for(j =0; j <256;j++) { double temp =0.0; if(i-1>=0) temp = temp + Xst_0[i-1][j]; if(j-1>=0) temp = temp + Xst_0[i][j-1]; if(i-1>=0&& j-1>=0) temp = temp - Xst_0[i-1][j-1]; temp = temp + i * p_histogram[i][j]; Xst_0[i][j]= temp; }
double Yst_0[256][256];//存储y方向上的均值矢量 Yst_0[0][0]=0* Pst_0[0][0]; for(i =0; i <256;i++)//计算y方向上的均值矢量 for(j =0; j <256;j++) { double temp =0.0; if(i-1>=0) temp = temp + Yst_0[i-1][j]; if(j-1>=0) temp = temp + Yst_0[i][j-1]; if(i-1>=0&& j-1>=0) temp = temp - Yst_0[i-1][j-1]; temp = temp + j * p_histogram[i][j]; Yst_0[i][j]= temp; }
int threshold1; int threshold2; double variance =0.0; double maxvariance =0.0; for(i =0;i <256;i++)//计算类间离散测度 for(j =0;j <256;j++) { longdouble p0 = Pst_0[i][j]; longdouble v0 = pow(((Xst_0[i][j]/p0)-Xst_0[255][255]),2)+ pow(((Yst_0[i][j]/p0)-Yst_0[255][255]),2); longdouble p1 = Pst_0[255][255]-Pst_0[255][j]-Pst_0[i][255]+Pst_0[i][j]; longdouble vi = Xst_0[255][255]-Xst_0[255][j]-Xst_0[i][255]+Xst_0[i][j]; longdouble vj = Yst_0[255][255]-Yst_0[255][j]-Yst_0[i][255]+Yst_0[i][j]; longdouble v1 = pow(((vi/p1)-Xst_0[255][255]),2)+pow(((vj/p1)-Yst_0[255][255]),2);
variance = p0*v0+p1*v1;
if(variance > maxvariance) { maxvariance = variance; threshold1 = i; threshold2 = j; } }
//printf("%d %d",threshold1,threshold2);
return(threshold1+threshold2)/2;
}
|
总结: 二维otsu算法得到一个阈值,然后对图像做二值化.仍然不能解决光照不均匀二值化的问题.比一维otsu效果好一些,但不是很明显.这个算法的亮点在于考虑的点的附近区域的均值.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号