转:http://www.52nlp.cn/unconstrained-optimization-one
估计有些读者看到这个题目的时候会觉得很数学,和自然语言处理没什么关系,不过如果你听说过最大熵模型、条件随机场,并且知道它们在自然语言处理中被广泛应用,甚至你明白其核心的参数训练算法中有一种叫LBFGS,那么本文就是对这类用于解无约束优化算法的Quasi-Newton Method的初步介绍。
事实上,这个系列的作者是我的师兄jianzhu,他在中文分词、语言模型方面的研究很深入,如果大家对于srilm的源代码感兴趣,可以参考他个人博客上写的“srilm阅读文档系列”,很有帮助。我曾经向他约过稿,他说业余时间在学数学,比较忙,还以为他没有时间给52nlp写文章,没想到今天晚上他突然交给了我这篇文档,比较长,我会分几部分陆续放在博客上。这里非常感谢他对52nlp的支持,以下内容作者为jianzhu。
本篇文档主要介绍无约束最优化问题,同时初步介绍解该类问题目前常用的一种算法即Quasi-Newton Method (拟牛顿法)。在介绍无约束最优化问题之前,我们首先会从直观上引入无约束最优化的概念,并在此基础上引入解这类问题的两个重要概念:步长和方向。由步长的选择引入重要概念line search,由方向的选择引入重要概念Quasi-Newton Method。因此本篇介绍文档主要分为以下几个部分:无约束最优化问题引入,Line Search ,Quasi-Newton Method和算法总结。
1.无约束最优化
对无约束最优化不熟悉的读者也许要问,什么是无约束最优化。这里以一个例子来说明该问题。
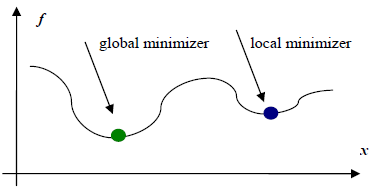
上图所示为一元函数f(x)的图像,无约束最优化问题,即不对定义域或值域做任何限制的情况下,求解函数f(x)的最小值,上面显示两个最小值点:一个为全局最小值点,另一个为局部最小值点。受限于算法复杂度等问题,目前大部分无约束最优化算法只能保证求取局部最小值点。这时读者不免要问,既然只能求取局部最小值点,那为什么这类算法还能应用呢。这是因为实际应用中,许多情形被抽象为函数形式后均为凸函数,对于凸函数来说局部最小值点即为全局最小值点,因此只要能求得这类函数的一个最小值点,该点一定为全局最小值点。
理解了上面的无约束最优化问题之后,我们就可以开始介绍无约束最优化的求解过程了,对于无约束最优化的求解首先我们需要选择一个初始点x_0,如下所示:
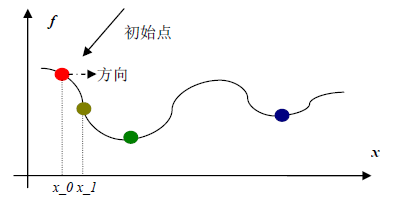
初始点选择好之后,就可以按照各种不同的无约束最优化求解算法,求解最小值点了。求解过程中主要涉及两个概念,即从初始点开始沿“哪个方向”以及“走多远”到达下一个点处。所谓“走多远”即之前提的“步长”的概念,“哪个方向”即方向概念。
2.Line Search
Line search主要用于解决之前提到的步长的概念,即方向确定好之后,需要确定从当前点x_k沿着该方向走多远,以便走到下一个合适的点x_k+1。若用p_k代表从第k个点走向第k+1点的方向,x_k代表当前点,x_k+1代表下一个点,a_k代表步长,则存在如下的等式:
x_k+1 = x_k + a_k * p_k (1)
这里简要介绍一下p_k,大部分line search方法要求p_k为下降方向,即从当前点沿着p_k方向移动后导致函数值减少。由于目标是求取一个函数的最小值,因此最优的情况是求取沿p_k方向满足f(x_k+1)为全局最小的a_k值,可用下式表示为:
Ø (a_k) = f(x_k+1) = f(x_k + a_k * p_k) (2)
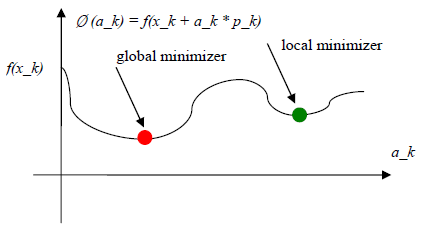
由于直接求取满足Ø (a_k)为全局最小值的a_k涉及到大量f(x_k + a_k * p_k)的计算,若从求导角度计算最小值,还会涉及到▽f_k+1的计算,计算量较大。因此从计算量角度考虑,可以采用如下较为折中的策略。
方向确定好之后,每一步的line Search主要涉及两个问题:1)什么样的a_k是合理的 2)如何选择a_k的长度。下面将沿这两个面展开讨论,首先讨论“什么样的a_k是合理的”,确定了该问题之后,我们就可以在此基础上选择a_k了。
未完待续:无约束最优化二
注:原创文章,转载请注明出处“我爱自然语言处理”:www.52nlp.cn
本文链接地址:http://www.52nlp.cn/unconstrained-optimization-one




