【转】推荐系统入门实践：世纪佳缘会员推荐

版本	作者	联系	日期
1.0	周巍然	weiran.chow@gmail.com	20120723
2.0	严 程	supersteven198701@gmail.com	20120821
3.0	严 程	supersteven198701@gmail.com	20120831

 

摘要：

     本文以2011年举办的第一届数据挖掘邀请赛的"世纪佳缘会员推荐"赛题为例，尝试了5种排序方法来为新注册会员推荐容易受到亲睐的老会员。

     先看5种排序方法的测试结果，以便朋友们有针对性地浏览本文。

	基于5倍交叉验证 NKCG@10	基于training set验证 NKCG@10
随机模型		0.08659561709415893
基于投票加权的排序	0.5760898362334391	0.15788352658143304
基于投票加权平均的排序	0.6345833528026847	0.2571459631326702
SVM-Rank（投票加权平均+Profile特征）	0.6344312058678667	0.2570729864787669
基于威尔逊区间法的排序	0.6373419863408559	0.26356889450029836
基于贝叶斯平均的排序	0.6359828316337668	0.25369412463315366

     可以发现，基于威尔逊区间法的排序，目前针对该问题取得了最好的推荐结果。其中，基于training set验证是为了方便与随机模型结果对比。

 

说明：

     (1)本项目来自2011年举办的"第一届数据挖掘邀请赛"，笔者周巍然亲身参与了比赛的整个过程，本文1.0版为笔者周巍然在赛后根据自己的体会及他人经验整理而成。

            (2)  在周巍然的引导下，笔者严程开始涉足互联网推荐系统这一新兴而又实用的领域，将这次比赛的项目作为入门训练。在周巍然的一些改进思路下继续研究，同时也尝试引入Learning to rank方法、以及时下非常流行的各种排序算法（如Reddit评论排序算法），希望能够进一步提升推荐算法的性能，于是就有了2.0和3.0版。特别地，在3.0版中将前3种方法根据数学含义更名，笔者认为新的命名更为贴切。

            (3) 本文是本人有关互联网推荐系统设计的一次践行结果，本文适合作为初学者对推荐系统的入门实践练习。本文全部代码及测试数据可免费下载，有任何问题欢迎直接联系任一笔者。

 

其中，1.0版实现了"投票加权"的排序与推荐

           2.0版补充实现了"投票加权平均"和"基于SVM-Rank进行Learning"的排序与推荐

           3.0版补充实现了"基于威尔逊区间"和"基于贝叶斯平均"的排序与推荐，该方法思想来自于阮一峰老师的博客，特此感谢！

 

前言

   背景：Amazon的数百万图书，Netflix的10万部电影，淘宝的8亿件在线商品，以及数以亿万计用户的资料和行为记录……互联网公司最近十年的迅猛发展伴随着海量数据的积累。然而，在线用户常常面对过多的选择而显得无所适从。心理学研究证实这类情境下的用户有时做出放弃交易的决定，从而造成大量潜在的用户流失。统计技术的发展能够为在线服务商提供更有效的推荐算法，在帮助用户走出信息过载困境、改善用户体验的同时，还能够挖掘商品长尾、提升企业价值。在今天，用户不再局限于通过搜索引擎来寻找感兴趣的信息，推荐系统无所不在地为我们发现自己的潜在需求。

　　本文主题：推荐在社交网络中的应用同样受到业界重视【1,2】。目标是为世纪佳缘网站提供会员推荐的智能算法，改善会员推荐的精度，增加网站黏度。

   本文目标：通过算法设计提供一个推荐系统，该系统有潜力为世纪佳缘网站的新注册会员推荐潜在的老会员，使得这些老会员尽可能受到新会员的亲睐。

   本文内容：算法设计思路、算法具体设计及代码、算法优劣的评测指标、算法推荐结果。

 

问题定义

    世纪佳缘网站在会员访问其网站时，会按照一定规则在页面的特定位置，给会员A推荐（rec）他/她可能感兴趣的会员B，此时A仅仅能看到B的头像（真人照片）。如果A进入B的主页进行查看，则发生了点击（click），此时A能浏览B的详细资料。在浏览B的资料后，如果A觉得有进一步的兴趣，则会通过站内信件（msg）与B联络。会员A对同一会员B的click、msg行为有可能多次发生。同一会员B也可能被系统多次推荐给会员A。另外，会员A本身也可能被系统推荐给其他会员。

    通过构造有效的统计评分算法模型，评估给定的候选会员集合中哪些会员更容易获得特定会员 A 的青睐。例如，如果需要给会员 A 推荐（rec）某 10 名指定的候选会员，则构造的模型应该能够将 1-10 号候选会员按照一定的优先级排序，排在前面的会员被认为更容易获得 A 的喜爱，从而引起 click（点击查看会员资料） 或 msg（给该会员发站内信） 的行为。根据推荐效果为事件进行排序： msg > click > rec，对应到评分算法模型中时，其权重依次减小。

 

评测指标

    性能良好的评分模型，应该能够给予那些引起msg或click的候选会员更高的评分（排序靠前），从而推荐给指定会员。本次竞赛的主要排名标准为Learning to Rank 问题领域广为使用的Normalized Discounted Cumulative Gain（NDCG）【3】。

    与经常用来比较两个序之间的相关程度的肯德尔和谐系数相比，NDCG指标的不同之处在于，它更强调和关注两个序中排名靠前的部分的相关程度。这与本次竞赛项目的实际需求正好相符，因为我们更希望将与会员 A 有可能发生 msg 行为的候选会员排名靠前。

         NDCG数学定义如下：

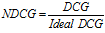
     这里 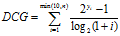。 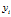表示模型给出的排序中，排名为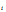的候选会员的实际 ACTION 值（msg=2，click=1，rec=0）。 对每一位获得推荐建议的会员 A，都需要计算一个相应的 NDCG。所有获得推荐建议的会员对应的 NDCG 的平均值，作为排名的主要依据。

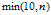     表示计算 NDCG 时仅采用排序前 10 的候选会员的 ACTION 进行计算，因此将尽可能多的 msg 或 click 排在前面至关重要。指数变换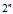是为了增大ACTION 间的差异以凸显msg和click 的重要性。折扣因子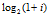用来强调越能将 msg 会员排名靠前的算法越好。例如，两种不同的推荐算法给出的排序对应的真实 ACTION 如下表所示，由于 RANK 1 算出的 NDCG 为 0.8045，而 RANK 2算出的 NDCG 仅有 0.7579，我们认为 RANK 1 对应的算法更好。

     这里给出一个计算 NDCG 的例子。假设某统计评分模型对 5 位会员进行了评分，以确定哪位会员更可能获得会员 A 的青睐（评分越高表示兴趣越大）：

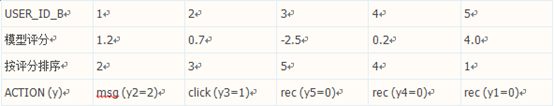
     因此对于会员A，

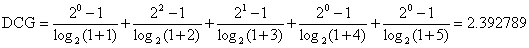
     如果能够获得的评分足够理想，从而能够完美地预测出会员A关于5位会员的兴趣排序，则此时相应的DCG称为Ideal DCG：

     从而对会员A，

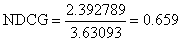
     NDCG的详细使用说明见"NDCG的示例程序.txt"。

 

数据说明

     本文提供了世纪佳缘网站中某城市会员在最近三个月内完整的交互行为数据 以及相关会员资料。共包含 4 个数据集：train.txt，profile_f.txt，profile_m.txt 和 test.txt。

train.txt 包含约 860 万条交互记录，每条记录包括 4 个属性，涉及近 6 万名会 员。格式如下：

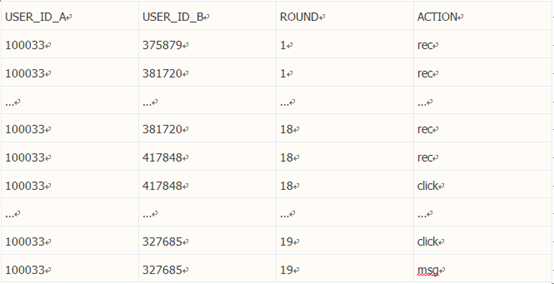
     在上例中，该网站在第1轮推荐中为会员100033推荐了会员375879，但会员100033并没有点击会员375879的资料进行查看（rec），系统也没有将会员375879再次推荐给会员100033。同样在第1轮中，会员381720被推荐给会员100033，虽然没有被点击，系统仍然在第18轮推荐在再次重复了这一推荐。在第18轮推荐中，会员100033在获得推荐后，仅仅查看了会员417848的资料（click），但没有进一步的行为。在第19轮推荐时，会员100033在查看了会员327685的资料后，发出了站内信件（msg）。对同一会员的不同推荐批次间存在时间顺序，即：第2批推荐发生的时间要晚于第1批推荐发生的时间。两批推荐之间的时间间隔由很多因素决定，通常取决于会员登录网站的频率，以及浏览不同页面的数量等。这些因素还会影响会员获得的推荐批次总数。

     一般而言，同一位会员B会被推荐给多位不同的会员，也可能在不同批次中，多次被推荐给同一位会员A。另外，A没有点击B的资料进行查看（rec），通常是由于多种原因造成的。有可能A对B的第一印象（推荐列表中显示的头像）不佳，或者A对在即将下线时获得的推荐不予理睬，又或者是A已经找到合适的交往对象而对其余推荐置之不理，甚至是会员当时的心情，都有可能造成rec（即不发生click）。总之，婚恋网站的用户浏览行为具有较大的随意性，多次推荐同一会员有时会增加点击的概率。对rec类样本的深入分析或许有助于提升推荐系统性能。

     在实际情况中，两位会员间较少发生多次msg的行为，这可能是经过线上交流后的两位会员常常会转为线下交流的原因造成的（如在站内信件中互留联系电话等）。参赛队可以自行通过数据证实或分析这一点。对线上多次发生msg交流的样本进行分析能否提升模型性能，尚不明确。

     男女会员资料（包括部分择偶要求）分别记录在profile_m.txt和profile_f.txt中。每位会员包含34个特征变量（feature），我们提供了字段列表来说明不同特征变量的含义。

test.txt 文件中包含了用来在线验证推荐算法效果的会员配对（interaction），及每对会员在三个月内的推荐次数。比赛过程中，为防止过度拟合现象的发生，竞赛排名系统仅仅从test.txt中随机选择约40%的USER_ID_A及相应样本进行NDCG的计算，据此进行排名。在竞赛结束后，系统会基于所有会员配对重新计算各参赛队模型的NDCG，并给出最终排名。由于比赛结束后无法再进行在线算法测评，因此本文算法改进主要基于train.txt进行交叉验证来进行测评。

     注意：本数据集由上海花千树信息科技有限公司提供，仅能用于本次竞赛的分析、建模用途。不得用于任何其他商业用途。以学术研究和论文发表为目的的，请与上海花千树信息科技有限公司联系并获取授权。竞赛委员会不具有授权权力。

 

解决方案

  数据准备

     为选取合适的数据进行模型训练与测试，需要将train.txt中的数据，基于5倍交叉验证思想，按照4:1随机分配，4份用于模型训练（命名为train_train.txt），1份用于模型测试（命名为train_test.txt）。

该步骤使用到了附件代码中的splitdata.py，通过给定不同的k值，实现5种不同的数据4:1分配方式。

  评分模型测评方案

      本文使用了2种方式来对比测评本文提出的模型效果。

    第一，按照一般性的数据挖掘模型验证方法，为防止过拟合【4】，需要使用5倍交叉验证中的1份数据来测试模型，给出相应测评分值。为方便介绍，本文仅以k=2这一种条件得到交叉验证所需数据，进行后续的模型训练与测评（由于处理过程的随机性，k取其它值的结果相差不大）。

     第二，为与竞赛官方提供的随机推荐模型给出的测评分值进行对比，以体现本文设计的模型效果，需要使用整个train.txt数据集测试模型，并给出相应测评分值。

  评分模型测评示例

     这里以第二种测评方式来说明，根据某种具体的评分模型，得到用户推荐顺序后，如何评测模型性能。

     基于附件代码中的label_train.py和train.txt，得到结果文件label_train.txt，该文件中包含针对每个新用户userA的推荐用户的action列表userB_Action_List。文件中每行按照userA升序排列，针对userA推荐的每个userB，可能存在多个action值，仅给出权重最高的action值（msg=2，click=1，rec=0）。

     假定基于某种模型，得到train.txt中每个新用户userA的推荐用户列表排序文件model_ranks.txt，该文件中每行同样按照userA升序排列，与label_train.txt中相对应。

     于是，基于附件代码中的evaluate.py、label_train.txt和model_ranks.txt就可以计算分别得到 NDCG@10和NDCG@20分值。例如根据附件NDCG_Example中的示例文件和程序，得到随机模型的NDCG@10和NDCG@20分值分别为：

(0.08659561709415893, 0.11637114804038115)

  评分模型设计

     本文所涉及的问题是一个典型的信息排序问题，通过排序先后给出推荐结果顺序。

    由于数据存在稀疏性及冷启动问题，也就是对新注册的用户进行推荐，这是本问题最大的难点。 针对稀疏数据和冷启动的数据特性，经典的算法诸如，最近邻的协同过滤算法、PageRank 排序算法、E-Greedy 排序算法、关联规则挖掘等并不太奏效，因为对于新注册的用户没有用户行为可分析。

     而最直接的想法是，根据分别记录在 profile_m.txt 和 profile_f.txt 中男女会员资料（包括部分择偶要求），其中每位会员包含 34 个特征变量（feature）。在考虑到特征之间的择偶要求是否匹配，建立一个回归模型，根据会员 A 和会员 B 的交互行为进行评分，如 msg 给出2分，click 给出1分，rec给出 0分，然而这样做收效甚微。事实上，因为人的行为太随机了，而且人往往重相貌高于其他， 不会仅仅因为你年龄、身高符合要求就和你 msg。profile可能并不奏效，用户行为才是真正值得我们挖掘的信息。

    大众受欢迎度 + 少量的 profile 信息也许是解决冷启动问题的最佳方式【5】。但本文同样尝试了另外两类流行的方法。一类是，结合基于投票加权平均的大众欢迎度和少量Profile特征作为特征向量，利用SVM-Rank进行排序的方法，以便了解利用用户Profile信息之间的配对是否能够进一步提高推荐效果。另一类是，借鉴时下非常流行的2个著名网站的评论排序算法（Reddit评论排序算法、IMDB电影热门度排序算法）来尝试提高推荐效果。

 

以下分别介绍5种模型方法的设计思路。

 

(1) 基于投票加权的大众欢迎度（代码见：version1(weighted votes)）

       Train.txt中第二列为被推荐用户，这些用户大多为老用户。根据这些用户被推荐的历史记录，按照一定的模型，可以得到每个老用户受大众欢迎的程度。该模型定义如下：

Popularity = msg_weight * msg_times + click_weight * click_times + rec_weight * rec_times

   上式中各参数含义非常明确，分别表示3种行为（msg|click|rec）的权重与次数的加权和。很容易理解，某个老用户被rec，click，甚至msg的次数越多，某种程度上就说明该用户更加受到公众的喜爱，三种行为的权重顺序为msg > click > rec，依次取值100，10，1。

  基于上述模型和train_train.txt，就可以得到多数老用户的大众欢迎程度。由于采用随机分配原则，train_train.txt中的大部分老用户，同样会出现在train_test.txt中。有了这些老用户的大众欢迎度排名，针对train_test.txt中的大部分被推荐用户，就可以根据相应的大众欢迎度进行排名，如果某个用户没有出现在train_train.txt中，则采用设置popularity为0的简单处理办法。最终可以得到针对train_test.txt中userA的推荐用户顺序列表文件myranks_train_test.txt。然后根据上述评分模型评测方法，可以计算得到本模型针对train_test.txt的NDCG@10和NDCG@20分值：

(0.5760898362334391, 0.6026498518875004)

    同理基于该模型可得到针对train.txt中userA的推荐用户顺序列表文件myranks_train.txt。然后根据上述评分模型评测方法，可以计算得到本模型针对train.txt的NDCG@10和NDCG@20分值：

(0.15788352658143304, 0.19271909879690152)

 

(2) 基于投票加权平均的大众欢迎度（代码见：version2-1(average weighted votes)）

   基于投票加权的大众欢迎度模型，仅考虑了每个老用户被推荐的总次数以及相应行为权重的加权和信息，但忽略了一个重要信息。例如，某2个老用户A和B的加权和相同，均为100，但用户A被推荐了20次，而用户B仅被推荐了10次，即用户B在更少的推荐次数内得到了同样的访问量。因此，我们可以认为用户B相对来讲拥有更高的大众欢迎度。

    基于这种思路，我们改进了上述模型，得到新的投票加权平均模型：

Popularity = ( msg_weight * msg_times + click_weight * click_times + rec_weight * rec_times) / (msg_times + click_times + rec_times)

    类似地，这里三种行为权重msg > click > rec，依次取值100，10，1。

   按照类似的处理步骤，基于该模型，针对train_test.txt中userA的推荐用户顺序列表文件myranks_train_test.txt。然后根据上述评分模型评测方法，可以计算得到本模型针对train_test.txt的NDCG@10和NDCG@20分值：

(0.6251315909409053, 0.6531515387910409)

    同理基于该模型可得到针对train.txt中userA的推荐用户顺序列表文件myranks_train.txt。然后根据上述评分模型评测方法，可以计算得到本模型针对train.txt的NDCG@10和NDCG@20分值：

(0.22950347745869737, 0.2728895216170754)

    在此基础上，当我们尝试针对三种行为使用不同的权重时，结果会有微妙的变化。最终，我们经验性地发现，当三种行为权重msg > click > rec，依次取值2，1.5，1时，能得到相对最好的结果，分别为：

(0.6345833528026847, 0.6619046966636642)

(0.2571459631326702, 0.30000037338792146)

     这里的0.25XXXX相比随机模型的0.08XXXX已经有了很大提升，足以说明本模型已极大地提升了推荐效果。

 

(3) 基于SVM-Rank（投票加权平均 + Profile构成特征） （代码见： version2-2(average weighted votes + SVM-Rank)）

     虽然上述基于大众欢迎度的评分模型已经极大地提升了推荐系统的效果，但至今我们没有使用过用户的任何Profile信息，而这些信息很有可能成为我们忽视的重要信息。

     从附件"数据库表.xlsx"中我们可以方便地提取一些重要特征字段，这些字段很可能会直接影响到用户userA是否会在查看某个userB的资料（click）后进而给他发送站内信息（msg）。这里我们提取了如下4个主要特征字段：

           Last_login：用户是否活跃（active），如果最近3个月都未登陆过，新用户可能不太会想跟TA联系；

          Status：用户是否处于征友状态（demand），如果已经在跟他人联系，将不易被推荐；

          Login_count：登陆次数（count），如果某个用户登陆次数太少，新用户可能会觉得跟他联系希望不大；

          Avatar：是否有头像（picture），虽然某些新用户不要求对方有头像，但如果有头像，肯定会起到加分的作用。

    再结合上述大众欢迎度（popularity），这里共计有5个特征，构成特征向量：

Feature_vector = （popularity，active，demand，count，picture）

    要想充分利用这些特征向量信息来训练一个有效的评分模型，最直接的想法就是利用一种用于排序问题的SVM方法：SVM-Rank。

         SVM-Rank这一方法是经典的Learning to rank问题中的一种重要方法【6】，传统的SVM方法是一种用于解决分类问题的机器学习方法，这里SVM-Rank通过将排序问题转化为分类问题，来间接实现某种信息的排序。

         要使用SVM-Rank，可以通过其官网【7】进行了解学习。该程序具备特定的输入与输出格式，以及某些重要的参数设置。其输入格式遵从Learning to rank问题领域的标准测试用数据集LETOR【8】的格式要求，如下所示：

      其中，第二列qid:n为某次查询的编号，这里共包含3次查询，每次返回4个结果。第一列为每次查询结果中对应4个结果的相对排序。后面依次给出了5个特征序号及对应的特征值。#后为注释信息，会被程序自动忽略。

             回到我们的问题，我们已经提取了5个特征，基于train.txt、profile_m.txt和profile_f.txt我们可以轻松获取每个老用户的特征向量。那么要利用SVM-Rank，就必须将这些特征向量按照给定的格式生成SVM-Rank训练和预测所需的文件。

            以5倍交叉验证的模型测评方式为例：

     首先，我们基于train_train.txt，利用上述投票加权平均的大众欢迎度模型计算多数用户的欢迎度排名user_popularity.txt。

     其次，基于user_popularity.txt，profile_m.txt和profile_f.txt计算大多数老用户的特征向量文件user_feature_vector.txt以及后面将被SVM-rank使用的预测数据集user_feature_vector_for_predict.txt。

     然后，按照给定的格式生成SVM-Rank训练模型所需的输入文件user_svm_train_file.txt，并使用SVM-Rank训练模型参数。需要注意的是，训练集中需要包含为每个用户userA推荐的用户列表的真实排序。为某个用户userA推荐一个包含N个用户的列表，就相当于一次查询，返回N个结果。作为训练集，这N个结果的排序必须是已知的。遗憾的是，竞赛中未能提供这样一种数据来反应所有老用户的实际排序，为此，我们只能采用上述大众欢迎度user_popularity.txt的结果来为这N个用户排序，以便构成训练集。

     最后，利用SVM-Rank和user_feature_vector_for_predict.txt预测大多数用户的分值，对所有用户的分值进行排序，就可以针对train_test.txt或train.txt得到所有被推荐用户的排序，进而得到模型的测评分值。

     基于该评分模型，针对train_test.txt中userA的推荐用户顺序列表文件myranks_train_test.txt。然后根据上述评分模型评测方法，可以计算得到本模型针对train_test.txt的NDCG@10和NDCG@20分值：

(0.6344312058678667, 0.661812638898174)

     同理基于该模型可得到针对train.txt中userA的推荐用户顺序列表文件myranks_train.txt。然后根据上述评分模型评测方法，可以计算得到本模型针对train.txt的NDCG@10和NDCG@20分值：

(0.2570729864787669, 0.300026754320666)

           与上述模型结果进行比较，发现将大众欢迎度与用户profile信息进行结合，采用Learning to rank的方法并不能对结果有明显提升。

 

(4) 基于威尔逊区间的大众欢迎度（代码见：version3(Wilson Interval)）

    上述基于投票加权平均的排序方法，是比较常规的依据经验设计的排序模型，而本小节将要介绍的基于威尔逊区间的排序算法是来源于具备强大理论基础的统计学知识。

    最初接触到基于威尔逊区间排序是来自于阮一峰老师的博客【9】，其博客上先后连载了6篇不同的排序算法。其中，Delicious和Hacker News、Reddit、Stack Overflow及牛顿冷却定律等算法主要永固解决一定时间内的热门话题排序问题，排序受时间影响很大；而威尔逊区间及贝叶斯平均更为灵活，可以解决与时间无关的排序问题。

    本小节关注基于威尔逊区间的排序问题。大概原理根据阮一峰老师的介绍，再经过自己的整理介绍如下。

    首先将用户对某一话题或评论的投票问题进行如下假设：

• 每个用户的投票都是独立事件
• 用户只有两个选择，要么投赞成票，要么投反对票
• 如果投票总人数为n，其中赞成票为k，那么赞成票的比例p就等于k/n

     那么针对某个评论的大量用户投票事件就可以转化为一个统计学上的二项分布问题。在样本足够多，即投票数量n越大时，概率p可信度越大，如果p越高，就说明该话题越受欢迎，这没有问题。但问题出在对于某些话题投票数n相对太少，这时的概率p的可信度会大大降低，即使p很高，也不敢妄下结论说该话题非常受欢迎。

     根据以上假设，我们知道p是"二项分布"中某个事件（投赞成票）的发生概率，因此我们可以计算出p的置信区间。所谓"置信区间"，是指以某个概率而言，p会落在的那个区间。比如，某个话题的赞成率是80%，但是这个值不一定可信。根据统计学，我们只能说，有95%的把握可以断定，赞成率在75%到85%之间，即置信区间是[75%, 85%]。这样我们就可以得到一个根据置信概率确定排名的算法框架，分为以下三步：

• 计算每个话题的"赞成率"（即赞成票的比例）
• 计算每个"赞成率"的置信区间（以95%的概率）
• 第三步，根据置信区间的下限值，进行排名。这个值越大，排名就越高

     置信区间的实质，就是进行可信度的修正，弥补样本量过小的影响。如果样本多，就说明比较可信，不需要很大的修正，所以置信区间会比较窄，下限值会比较大；如果样本少，就说明不一定可信，必须进行较大的修正，所以置信区间会比较宽，下限值会比较小。

     现在话题的排名问题转化为计算二项分布的置信区间问题，统计学上广泛使用的"正态区间"方法只适用于样本足够多的情形。为了解决小样本的置信区间计算准确性问题，1927年，美国数学家 Edwin Bidwell Wilson提出了一个修正公式，被称为"威尔逊区间"，很好的解决了这个问题。基于威尔逊区间的置信区间计算公式如下：

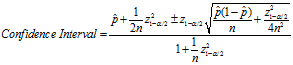
           上述公式中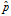，表示某一话题的"赞成票比例"，n表示样本大小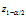，表示对应某个置信水平的z统计量，这是一个常量，可以通过查表得到。一般情况下，在85%和95%的置信水平下z统计值分别为1.0和1.6。

     威尔逊置信区间的下限值为：

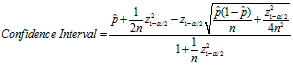
      可以看到，当n的值足够大时，这个下限值会趋向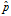。如果n非常小（投票人很少），这个下限值会大大小于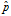。实际上，起到了降低"赞成票比例"的作用，使得该项目的得分变小、排名下降。

这就是目前Reddit评论使用的主要排名算法。

     现在回到我们这里所要面对的问题，即如何应用威尔逊区间法给出世纪佳缘会员的排名。威尔逊区间法将实际排序问题抽象为二项分布的统计问题，这里将世纪佳缘每个老会员看作一个话题，在过去有很多其他会员对他们进行了rec，click甚至msg三种操作，可以看作3种投票，所以无法直接应用威尔逊区间法进行排序。

     但是，根据经验，某个老会员被其它会员进行click或msg，都说明其它会员对这个老会员有一定好感，2种情形都可认为是"投赞成票"，而如果老会员仅仅是被系统推荐rec，说明其它会员不感兴趣，则可以认为是"投反对票"，由此，可以将问题转化为一个"二项分布"的统计问题。

      这里，我们给定三种事件rec，click和msg以不同的权重（分别为1，1.5，2），则对于某个老会员，

      赞成票数为：

Ups = msg_weight * msg_times + click_weight * click_times

      反对票数为：

Downs = rec_weight * rec_times

      那么投票的赞成率p = ups / (ups + downs)，于是就可以使用威尔逊区间法给出排序。

     具体在排序算法中的核心函数，即计算针对每个老会员的投票赞成率的置信区间时，参考率Reddit评论排序的开源代码【10】。

     基于该评分模型，针对train_test.txt中userA的推荐用户顺序列表文件myranks_train_test.txt。然后根据上述评分模型评测方法，可以计算得到本模型针对train_test.txt的NDCG@10和NDCG@20分值：

(0.6373419863408559, 0.6640676330359446)

     同理基于该模型可得到针对train.txt中userA的推荐用户顺序列表文件myranks_train.txt。然后根据上述评分模型评测方法，可以计算得到本模型针对train.txt的NDCG@10和NDCG@20分值：

(0.26356889450029836, 0.30645765290261523)

           与基于投票加权平均的排序模型结果进行比较，发现该模型仍有进一步提高。

 

(5) 基于贝叶斯平均的大众欢迎度（代码见：version4(Bayes Average)）

     除了威尔逊区间法之外，贝叶斯平均法【11】也非常适合于解决与时间无关的排序问题。威尔逊区间法很好地解决了投票人数过少、导致结果不可信的问题，但同时也存在一个致命问题，即马太效应：排行榜前列总是那些票数最多的项目，新项目或者冷门项目，很难有出头机会，排名可能会长期靠后。

     举例来说，一部好莱坞大片有10000个观众投票，一部小成本的文艺片只有100个观众投票。这两者的投票结果，怎么比较？如果使用"威尔逊区间"，后者的得分将被大幅拉低，这样处理是否公平，能不能反映它们真正的质量？一个合理的思路是，如果要比较两部电影的好坏，至少应该请同样多的观众观看和评分。既然文艺片的观众人数偏少，那么应该设法为它增加一些观众。

     基于这个思路，IMDB数据库在其网站的电影推荐功能中提出了贝叶斯平均法进行排序。具体计算公式如下：

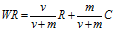
       其中，

                   - WR， 加权得分（weighted rating）

　　    - R，该电影的用户投票的平均得分（Rating）

　　    - v，该电影的投票人数（votes）

　　    - m，排名前250名的电影的最低投票数（现在为3000）

　　    - C， 所有电影的平均得分（现在为6.9）

    仔细研究这个公式，我们会发现，IMDB为每部电影增加了3000张选票，并且这些选票的评分都为6.9。这样做的原因是，假设所有电影都至少有3000张选票，那么就都具备了进入前250名的评选条件；然后假设这3000张选票的评分是所有电影的平均得分（即假设这部电影具有平均水准）；最后，用现有的观众投票进行修正，长期来看，v/(v+m)这部分的权重将越来越大，得分将慢慢接近真实情况。

    这样做拉近了不同电影之间投票人数的差异，使得投票人数较少的电影也有可能排名前列。

    把这个公式写成更一般的形式：

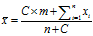
      其中，

　　    - C，投票人数扩展的规模，是一个自行设定的常数，与整个网站的总体用户人数有关，可以等于每个项目的平均投票数

　　    - n，该项目的现有投票人数

                  - x，该项目的每张选票的值

                 - m，总体平均分，即整个网站所有选票的算术平均值

     这种算法被称为"贝叶斯平均"（Bayesian average）。因为某种程度上，它借鉴了"贝叶斯推断"（Bayesian inference）的思想：既然不知道投票结果，那就先估计一个值，然后不断用新的信息修正，使得它越来越接近正确的值。

    现在回到我们这里要解决的问题，每个老会员可以被看作一个项目，所有新注册用户对某个老会员进行rec，click，msg可以看作不同评分（分别为1，1.5，2）的投票，每一次事件相当于一次投票。这样进行抽象后，就很容易利用贝叶斯平均法来解决我们这里的会员推荐问题。

     假定总的老会员数量为num，那么对于某个老会员i：

     投票人数n_i = msg_times + click_times + rec_times

     投票得分score_i = msg_weight * msg_times + click_weight * click_times + rec_weight * rec_times

     每个老会员的平均投票数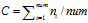

     每次投票的平均得分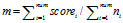

     基于该评分模型，针对train_test.txt中userA的推荐用户顺序列表文件myranks_train_test.txt。然后根据上述评分模型评测方法，可以计算得到本模型针对train_test.txt的NDCG@10和NDCG@20分值：

(0.6359828316337668, 0.6632682632885964)

     同理基于该模型可得到针对train.txt中userA的推荐用户顺序列表文件myranks_train.txt。然后根据上述评分模型评测方法，可以计算得到本模型针对train.txt的NDCG@10和NDCG@20分值：

(0.25369412463315366, 0.2963307946419093)

             与基于投票加权平均的排序模型结果进行比较，发现该模型推荐效果有一定提高，但略逊于基于威尔逊区间法的推荐效果。

      后记：在阮一峰老师的博客上，分析贝叶斯平均法的缺陷时，提到该方法是假设针对每个项目，用户的投票符合正态分布，如果实际的投票不符合这一假设，则推荐结果可能并不符合实际。对此，他推荐阅读William Morgan的"How to rank products based on user input"一文【12】，结合多项分布和贝叶斯平均法，通过估计每一分布期望的途径，有可能得到更符合实际情况的排序。通过仔细阅读该文，发现当使用简单的线性打分函数时，基于多项分布和贝叶斯平均法，与本文使用的第二种方法完全一样，也就是说，我们从统计学理论上为第二种方法找到了依据！

 

总结与讨论

    本文涉及互联网推荐系统领域广泛存在的冷启动问题，基于一些经典的推荐算法，如协同过滤、PageRank等并不奏效，于是采用基于大众欢迎度的投票算法来达到一定的推荐效果。最后在试图采用Learning to rank方法，充分利用用户的注册信息时，发现并没有给问题带来更好的解决效果。

    基于各种模型的测评分值如下表所示。

    具体每种模型算法的使用步骤见附件代码中的"run.txt"。

    目前，互联网领域最为广泛的推荐模式是联系用户与商品，即为某个注册用户推荐他可能感兴趣的某件商品，以便通过个性化推荐留住客户，提高流量的转化率、订单成交率。而本文的问题略有不同，是解决如何为用户推荐其他用户的问题。

   本文涉及到为新注册用户推荐他可能感兴趣的老用户，是典型的数据挖掘领域冷启动问题。在实际互联网应用中，用户的行为太过于随机，新用户是否对推荐的某个老用户感兴趣，可能完全凭借第一感觉，并不会严格根据某些资料配对（如身高、学历）来决定是否去了解一个老用户。因此，基于老用户在注册后积累的大众欢迎度或人气，来解决这里的冷启动问题，也许是相对最好的方式。

 

参考资料

1. TOBY SEGARAN，《集体智慧编程》， 2009
2. 项亮，《推荐系统实践》， 2012
3. http://en.wikipedia.org/wiki/Discounted_Cumulative_Gain
4. http://en.wikipedia.org/wiki/Overfitting
5. http://www.jiangfeng.me/blog/149
6. http://www.jiangfeng.me/blog/123
7. http://www.cs.cornell.edu/people/tj/svm_light/svm_rank.html
8. http://research.microsoft.com/en-us/um/beijing/projects/letor//
9. http://www.ruanyifeng.com/blog/2012/03/ranking_algorithm_wilson_score_interval.html
10. https://github.com/reddit/reddit/blob/master/r2/r2/lib/db/_sorts.pyx
11. http://www.ruanyifeng.com/blog/2012/03/ranking_algorithm_bayesian_average.html
12. http://masanjin.net/blog/how-to-rank-products-based-on-user-input