04 解链式法则和乘积法则

视频地址：https://www.bilibili.com/video/av10435213/

我们现在上一章节中，学习了幂次函数求导法和正弦函数求导。并且使用图像法更加直观的理解了这些运算过程。

当时想用这些求导公式在现实生活中运用，我们需要对这些公式进行混合、组合、调整。所以我们学习一下更复杂的组合函数如何求导。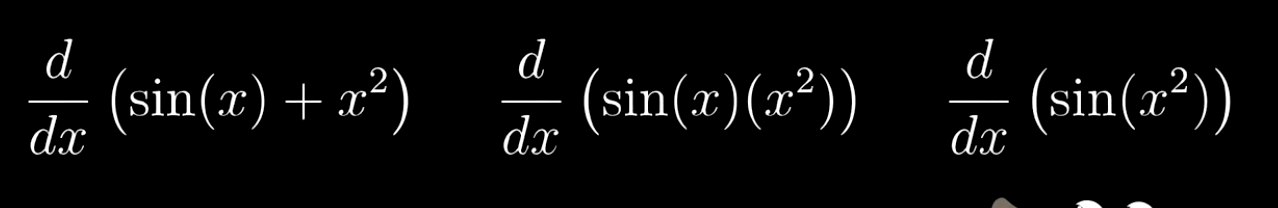

为了避免死记硬背，我们还是会使用一些像图像法这样更加直观的方式来理解这些公式。

上面包括了最常见的三种函数组合求导方式。函数相加求导，函数相乘求导，和复合函数求导。

了解了这三种求导方式，我们就能运用这三种公式将将一个复杂的组合一层一层的剥开，然后最终求得结果。

加法法则相对简单，我们先从这个法则开始：

现在我们将sin(x)和x²的函数曲线绘制出】那么，我们在坐标系中得到两个函数曲线，让后将每一个点上的值都相加我们会得到一个新的函数曲线就是f(x)=sin(x)+x²的函数曲线：

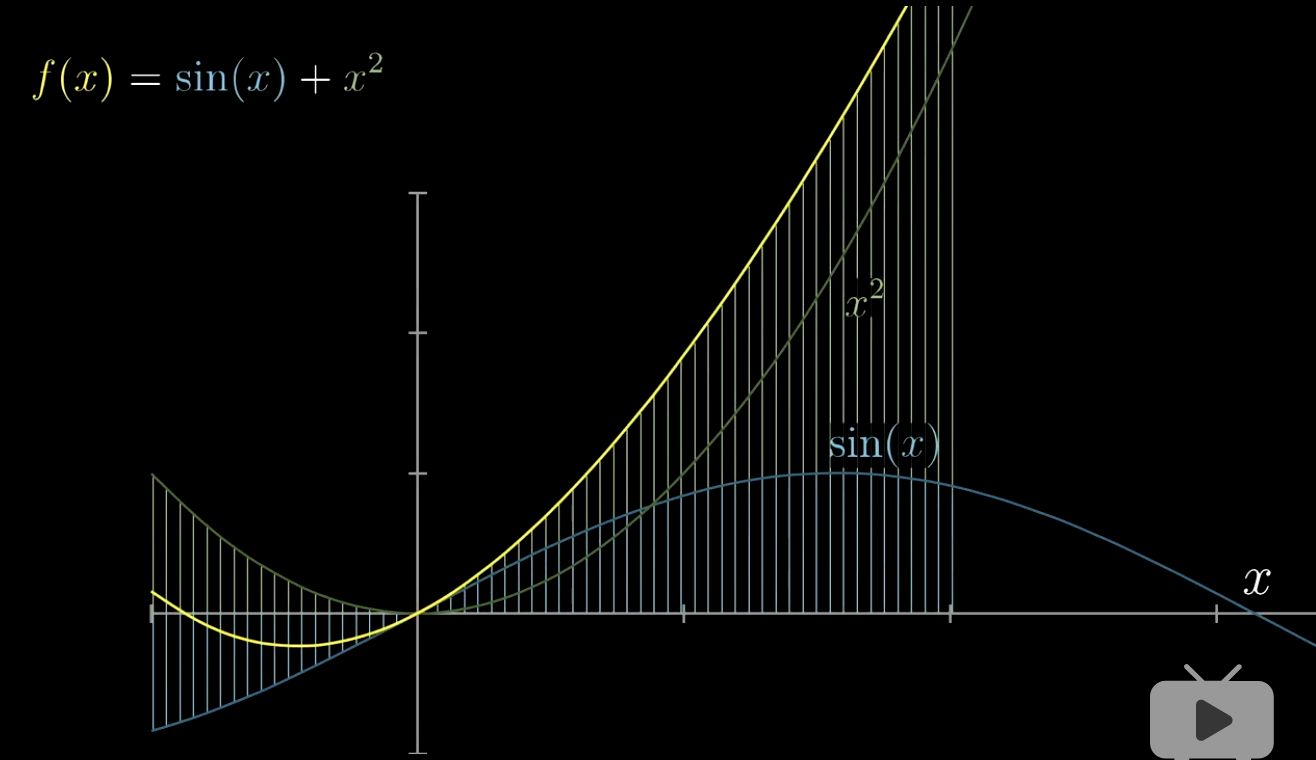
我们先取一个函数中一个点的值比如0.5，我们得到f(0.5)=sin(0.5)+0.5²

我们给x一个微小的变化值：dx那么df=d(sin(x))+d(x²)

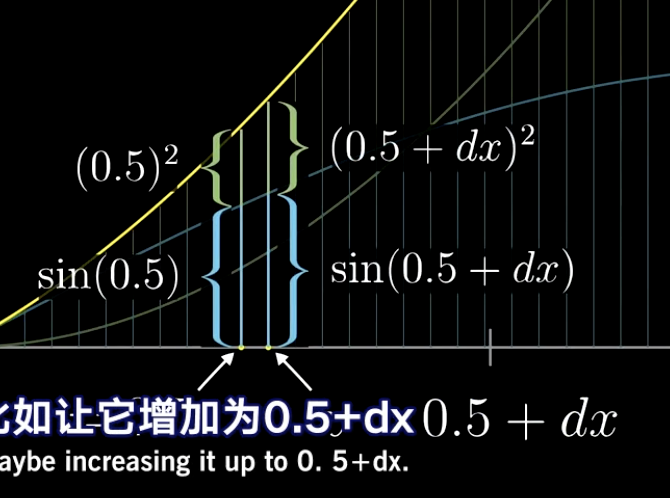
df/dx=d(sin(x))/dx+d(x²)/dx：

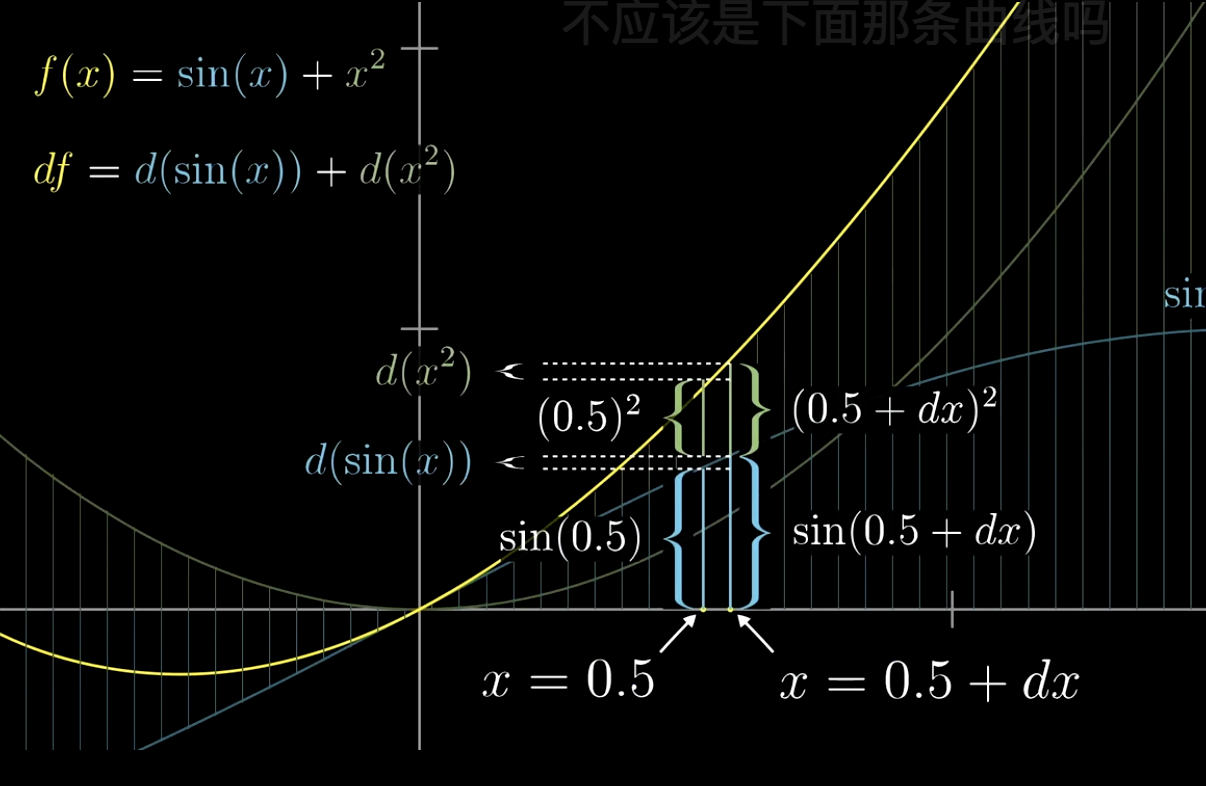
由此我们可以清晰的看到求导的加法法则：

 

不过乘积法则可不是是类似规律d(f(x)*g(x))≠(dg/dx)*(dh/dx)

我们还是以sin(x)*x²为例子：

 

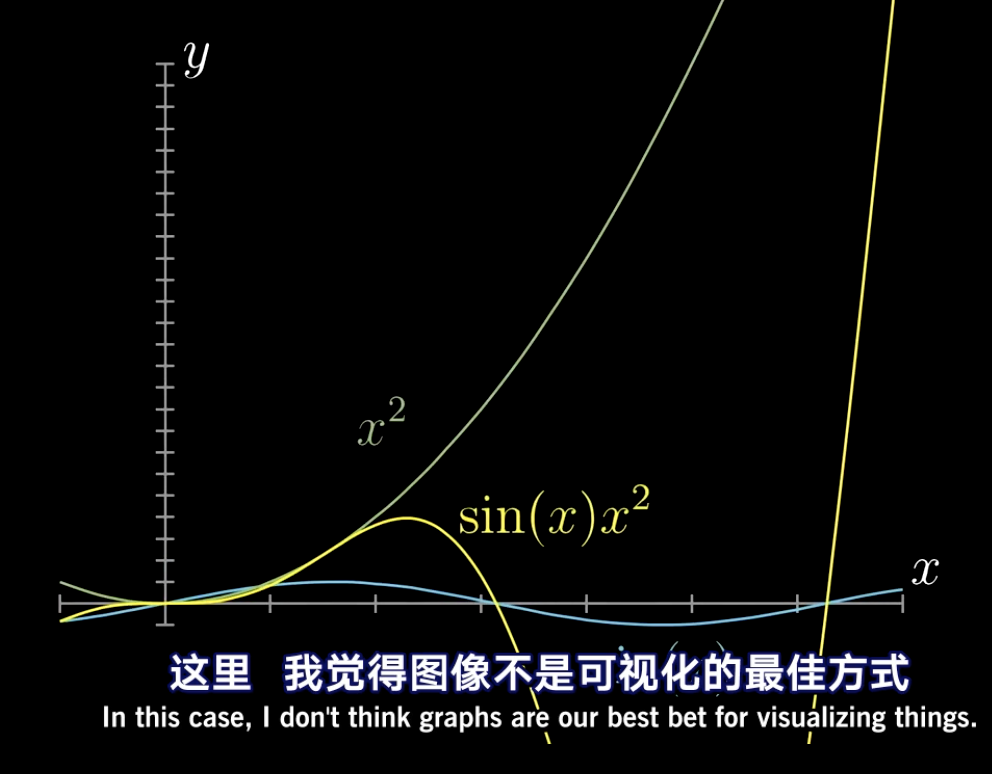
这个新得到的乘积函数曲线就没法像相加那么直观的找到规律了。

不过，面对两个数字相乘，在几何学上的意义正好是求矩形面积，使用这个方法，几何求解发也许能更加直观的理解乘积法则。

我们想象一个矩形，他的一个边随着x的变化呈现出正弦函数的变化规则，另外一个边则呈现出二次幂方程的变化规则：

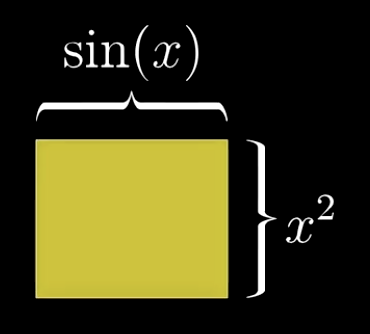
我们可以看到，f(x)随着x值的变化而产生的变化，与这个矩形面积随着x值的变化而产生的变化值是一致的。

不过，当x产生变化的时候到底发生了什么，好像还是不是很好理解。

我们在旁边加上一个标尺，标出随着x的变化，矩形形状的变化也许能更加直观一些当，值发生变化时：

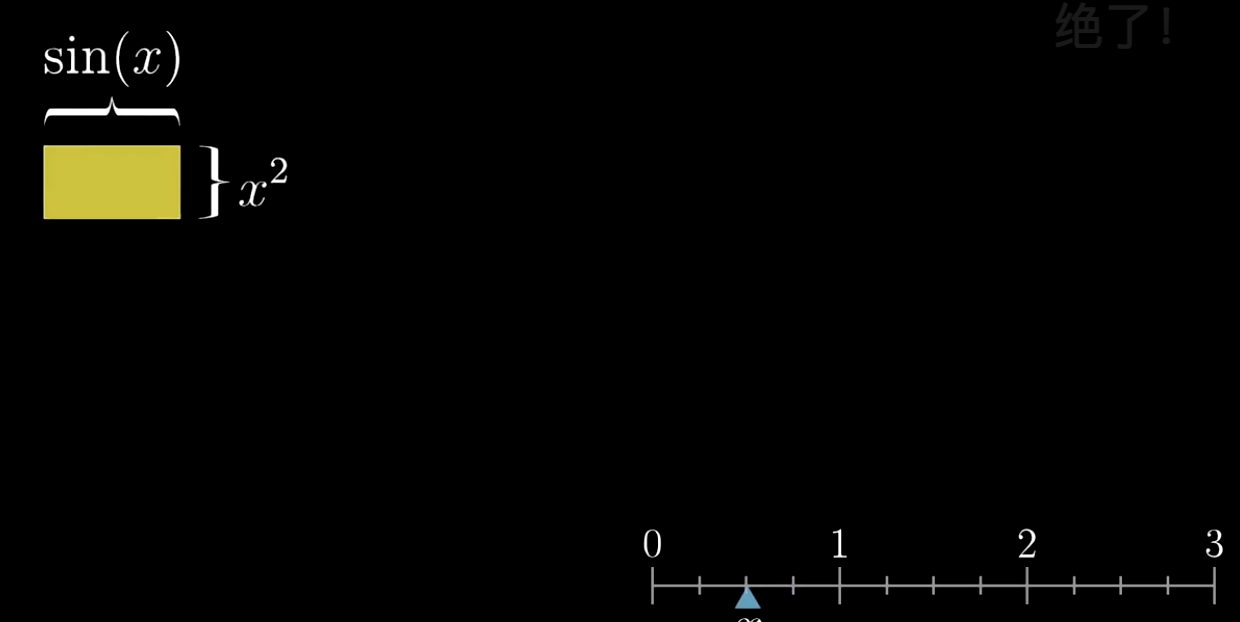
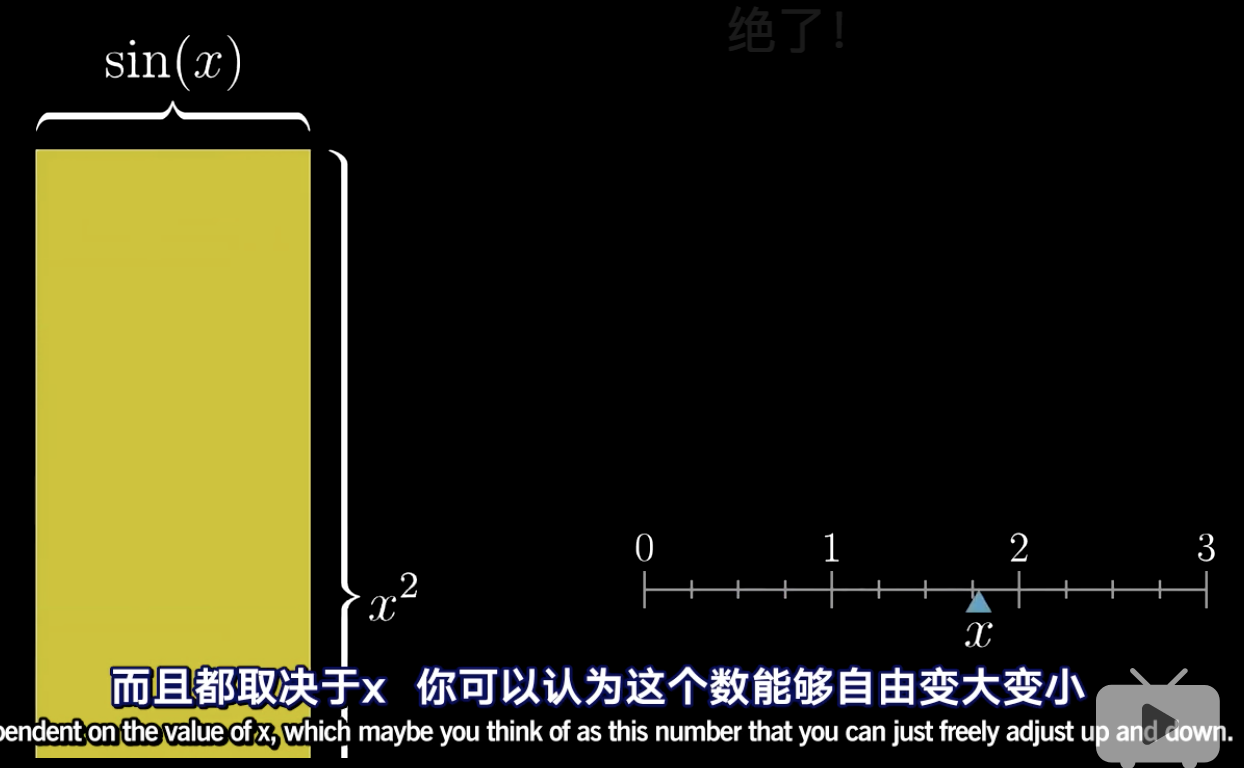
总之随着x的增加，一个边像正弦函数一样，在1到-1之间来回摆动。另外一个边则快速的以自身平方的速度增加。

那么当x的值产生一个微小的变化时，这个矩形的面积也随之产生了微小的变化：

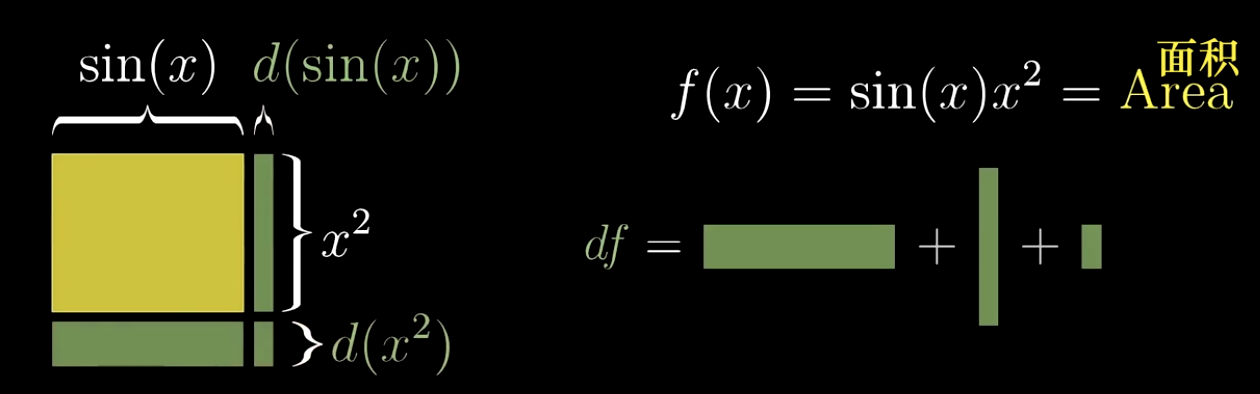
嗯，还是那个熟悉的味道。

图中右侧横着的绿色方块它的宽度就是sin(x)的值。高度是x²随着x的变化而产生的变化，也就是d(x²)。这个方块的面积就是sin(x)*d(x²)

图中右侧竖着的绿色方块它的宽高就是x²的值。高度是sin(x)随着x的变化而产生的变化，也就是d(sin(x))。这个方块的面积就是x²*d(sin(x))

而最右侧的小方块则再一次的被忽略。

那么总的面积变化就是sin(x)*d(x²)+x²*d(sin(x))，我们知道面积与f(x)是相等的则

df=sin(x)*d(x²)+x²*d(sin(x))

所以我们得到了乘积公式：

 

现在再来看复合函数。

 

我们拿f(x)=sin(x²)这个符合函数为例子。 

这回之前的两种方式都无法直观的用在这个函数上了。

将f(x)拆解一下。

f(x)=g(h(x)) 

h(x)=x²

g(x)=sin(x)

然后我们换一种可视化的方式来分析这个问题。

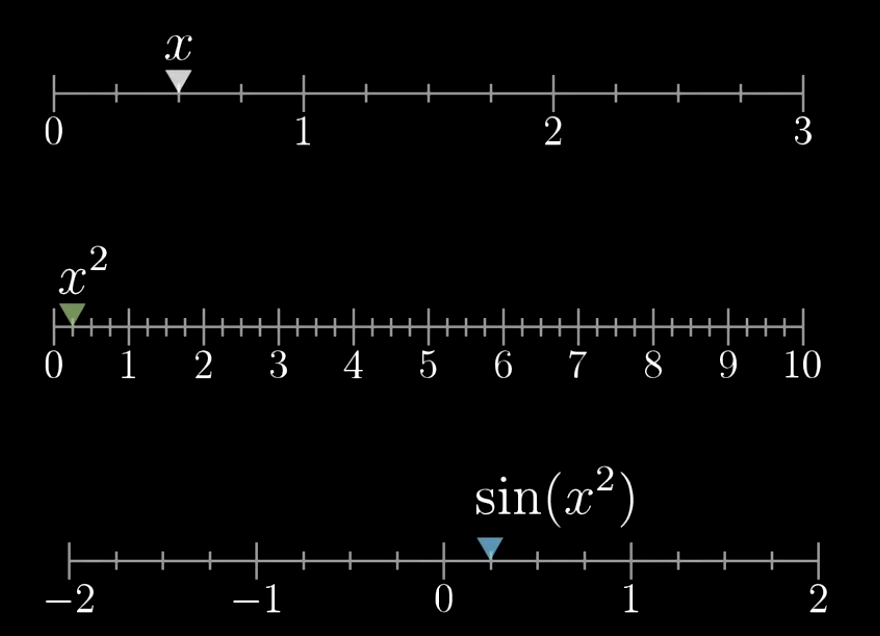
第一条线代表的是x的变化。

第二条线则是由对应的h(x)函数值。

第三条线是对应的f(x)函数值。

当x在原来的基础上产生了微小变化dx的时候。

在第二条线上产生的变化dh=2x*dx

这个变化再传导到第三条线，df=d(sin(h))=cos(h)*dh=cos(h)*2xdx=cos(x²)*2x*dx

df/dx=cos(x²)*2x

所以通过链式法则，我们看到，

dg(h(x))/dx=dh(x)*d(g(h(x)))

dg(h(x))/dx=(dg/dh)*(dh/dx)=dg/dx=dg/dx