03 几何法求导

视频链接：https://www.bilibili.com/video/av10396996/

 

这一节课，我们会用可视化的方式直观的思考导数公式的意义。

并鼓励你永远不要忘记，微小的变化才是导数的意义。

在一个公式f(x)中，当我们的x轴取值发生了dx的微小变化时，相应的在y轴产生了一个df的变化。

df/dx也就是这个变化的变化率。这就是导数的意义。

我们知道当f(x)=x²时，我们的变化率会随着x的增加而增加。

当x=0时，是切线斜率是0

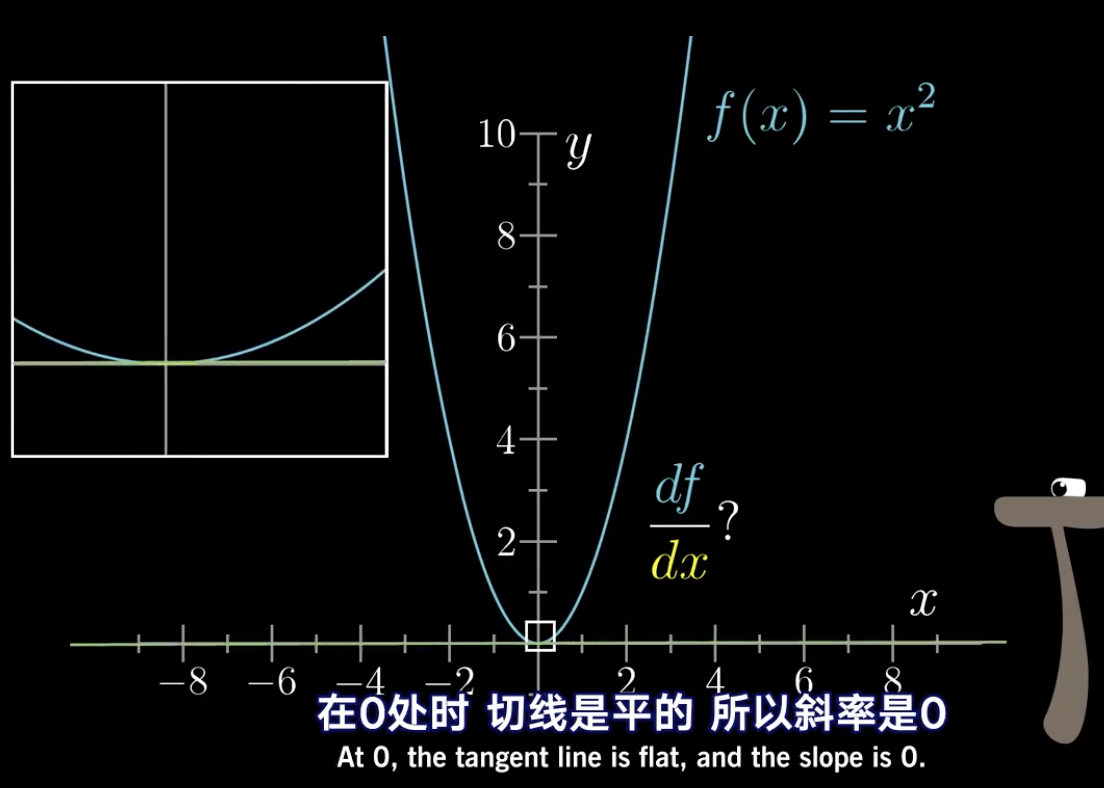
当x=1时，它的斜率稍微变得陡峭。

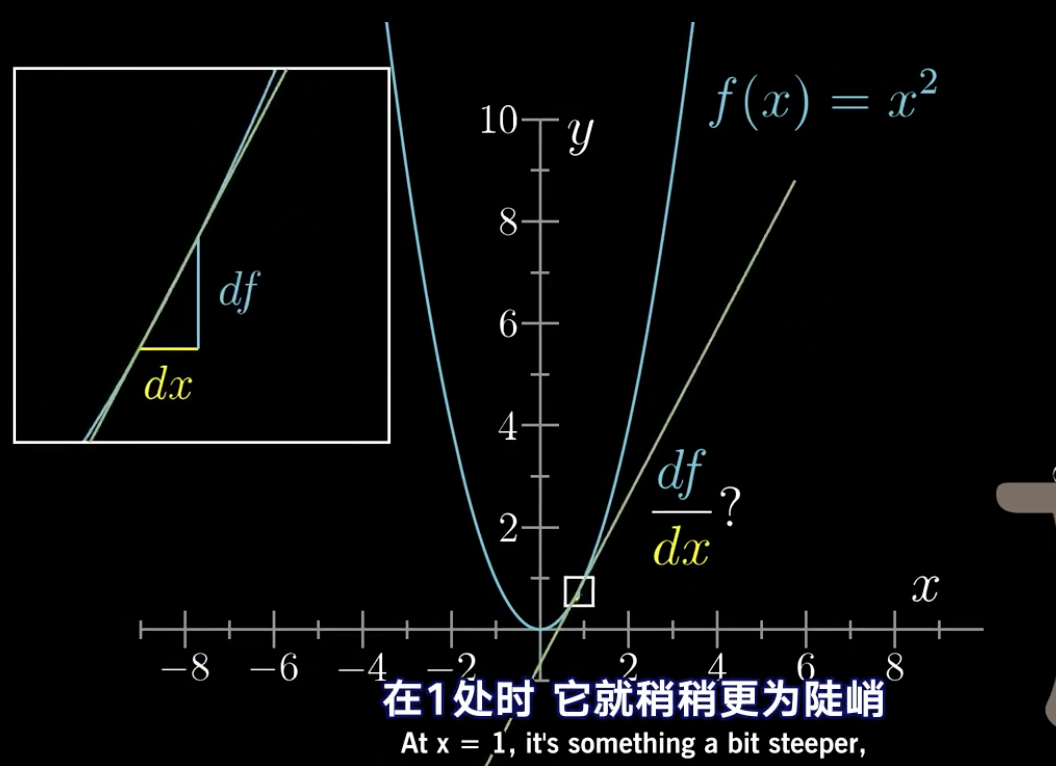
而随着x的增加，会越来越陡峭。

接下来我们用更直观的方式来理解。

x²，可以理解为一个边长为x的正方形面积。

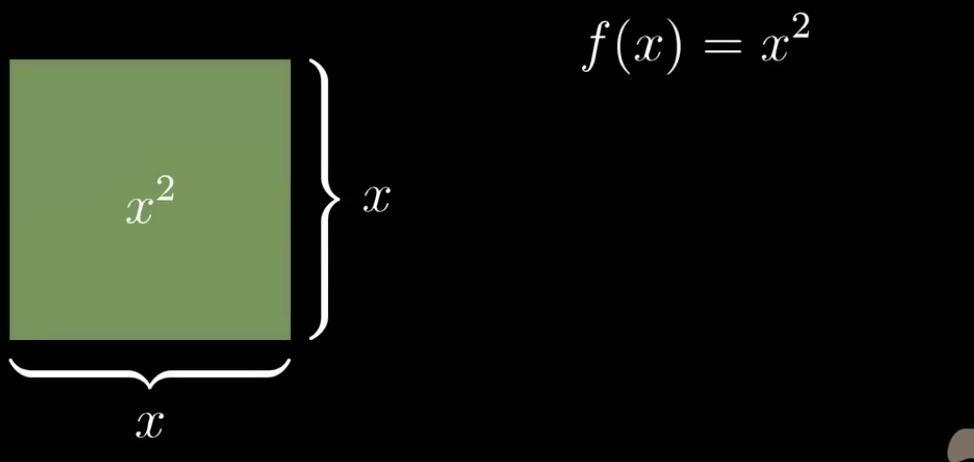
上图这个正方形，我们这个正方形设随着x增加的而增加的面积为df那么：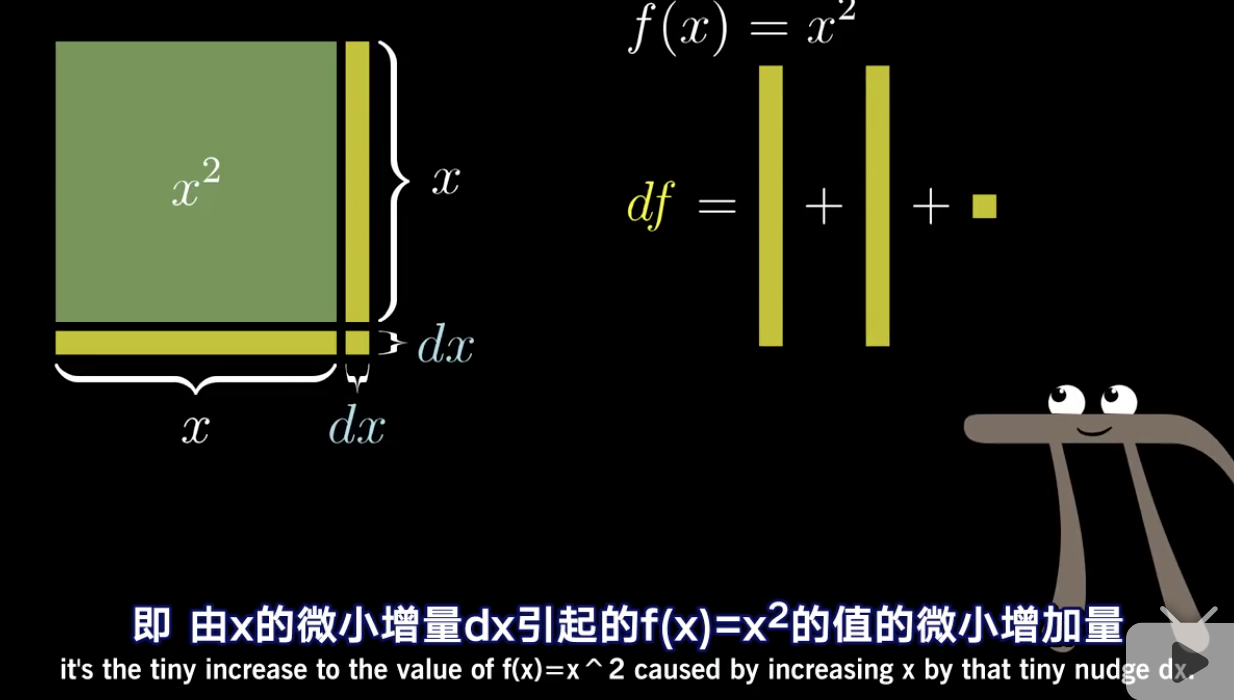

 

增加的面积为两个竖条的面积各自为：x*dx  而小方块的面积为: dx²

那么df=2x*dx+dx²

df/dx=2x + dx

当dx逐渐缩小，dx可以忽略不计。

我们就得到f(x²)的导数是 2x

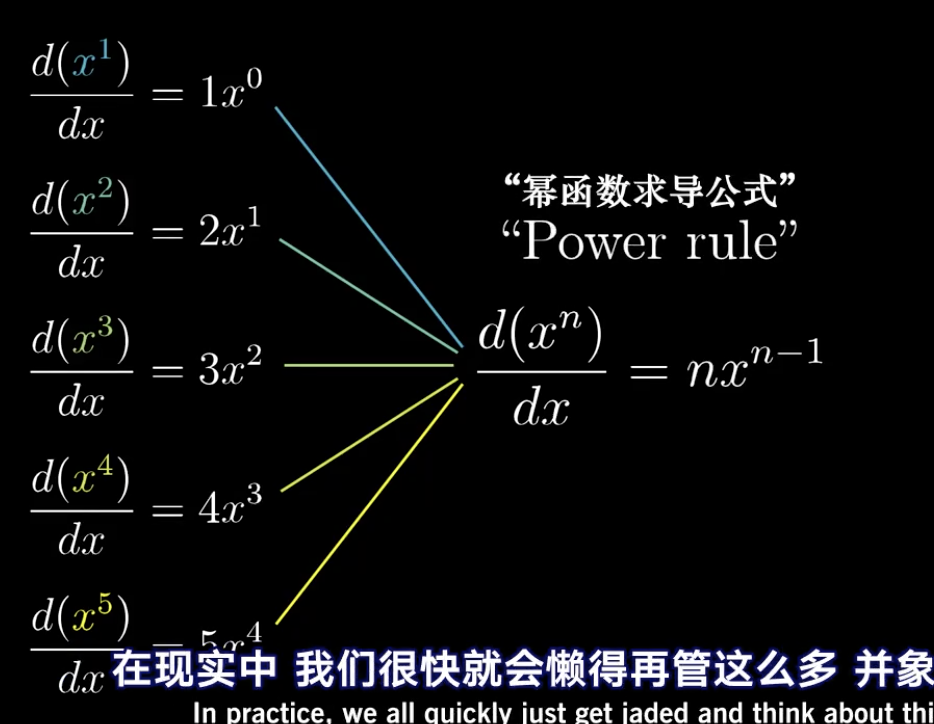
同样的道理可以直观的推导到三次方的公式上。

x³理解为一个边长为x的立方体。

用上面的方法可以很容易的直观想象出，为什么x³求导公式是3x²

但是x三次方以上的幂函数我们很难用几何图形的方式想象他的形状。毕竟我们的大脑是在三维空间中进化来的。

一下就是x的n次幂求导公式的推导。虽然不能直接用集合图形法来证明，

但是把这个公式中的各个相加的项与我们之前公式中的项相对应，还是可以帮助你更好的理解这个推导的过程。

而且图像法也可以告诉我们，数学公式是有现实意义的，并非只是纯粹的计算技巧。

 

课程中还给出了一个思考题：自己通过图形法推导1/x的导数。

视频中还给出了提示：

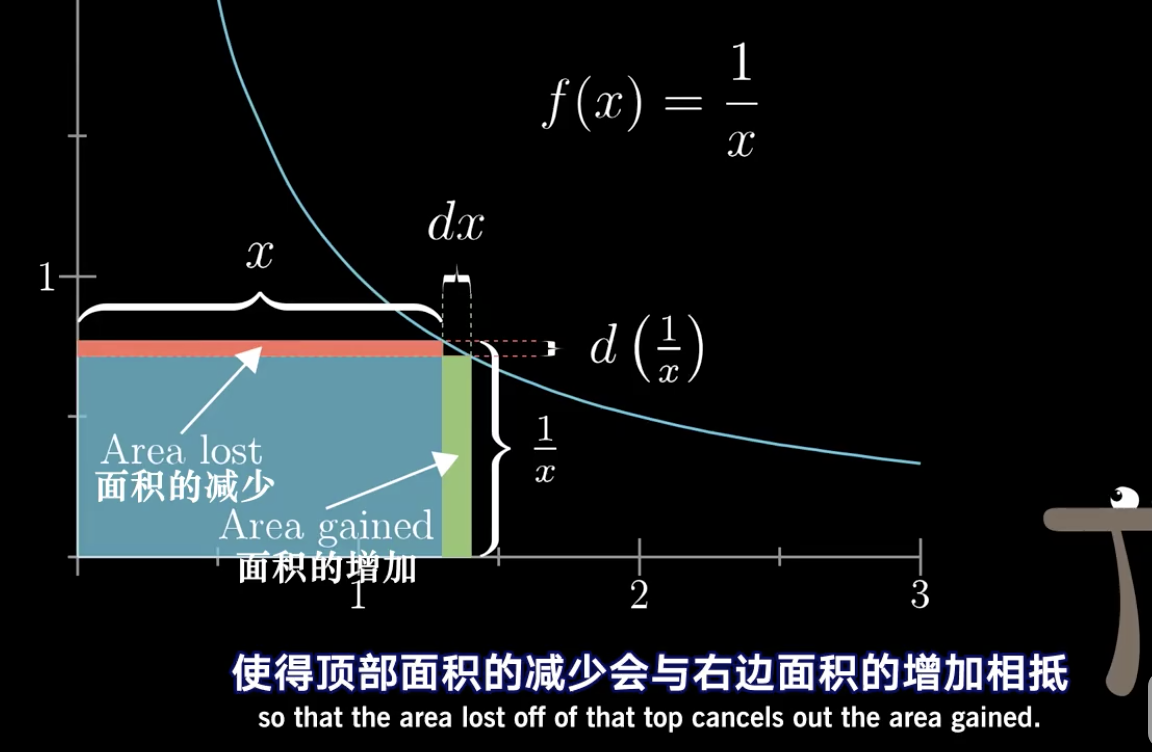
使用图形法，我们可以知道：1/x*x=1

这一点很明显。而1/x*x可以看做是一个底为1/x，高为x的矩形的面积。而这个矩形随着x的变化面积永远都为1

那么当x增加了dx时，右边的面积增加了途中绿色的部分，约等于1/x*dx，上面也就是红色部分的面积改变为df*x

因为该矩形的面积不变，所以

1/x*dx+df*x=0

df*x=-1/x*dx

df/dx=-1/x²

 

 

最后，我们来看看正弦函数的求导法。

关于正弦函数求导，视频中主要使用了单位圆进行辅助推导。

对单位圆不熟悉的可以先移步：
https://zh.wikipedia.org/wiki/%E5%8D%95%E4%BD%8D%E5%9C%86

不了解单位圆后面的证明看着可能会有些地方难以理解

我们先将sin(θ)的函数曲线绘制出来，然后看他的切线变化，大致得到这样一个图形。

当2π*n+π/2时，切线是平的。而当2π*n+π时，切线的斜率最陡峭。而且呈现出周期性。

这个形状与cos(θ)的函数很像。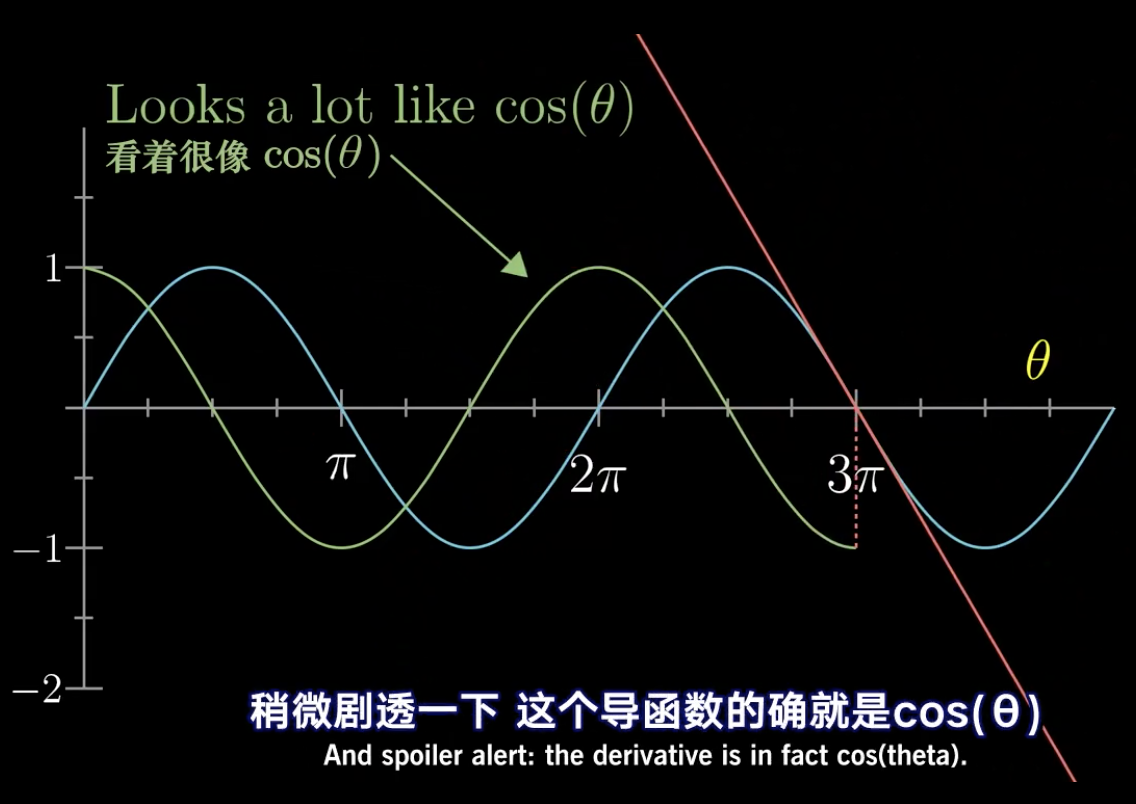

现在我们就用单位圆来看一下sin(θ)的求导公式是不是cos(θ)

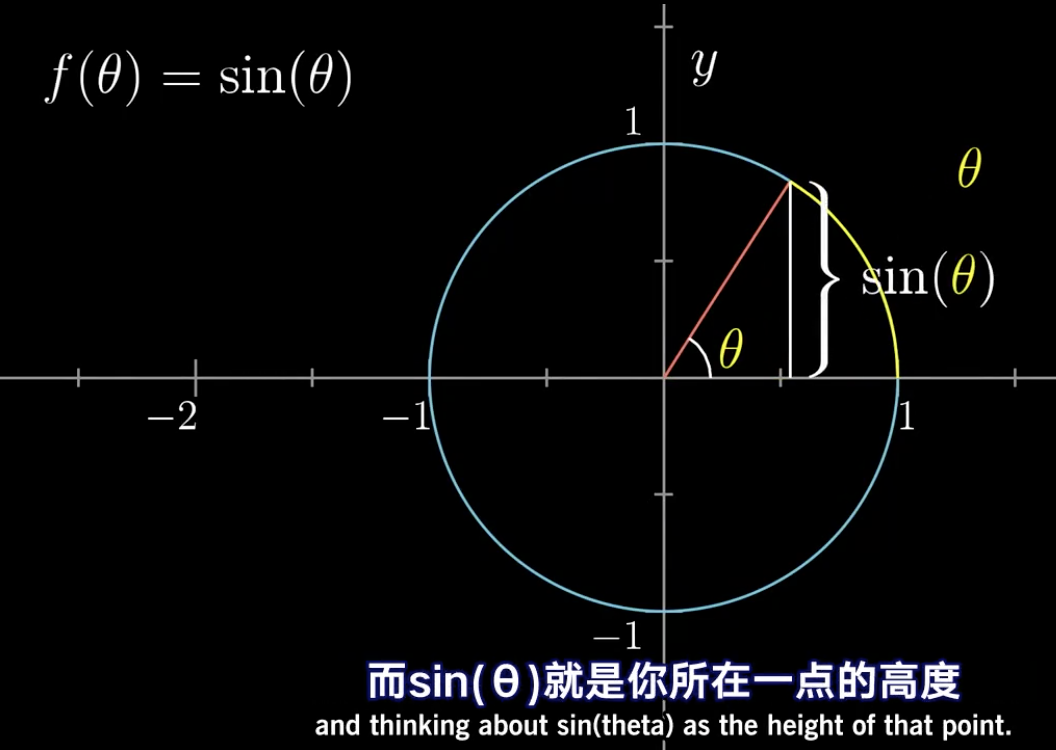
如图在单位园公式为x²+y²=1，随着θ的变化，y的值正好就是sin(θ)的值。

而θ的值与黄色的部分的长度也是相等的。

等等，为什么θ和值会θ角度下，对应的弧度长度一致呢？

其实很简单。因为x²+y²=1，绘制出的圆的半径为1。在这个图中可以很明显的看到这一点。

那么这个的周长就是2π。的变化是从0到2π随着θ的变化而均匀变化。

θ自身的变化也是从0到2π，均匀变化。很明显他们的值是一一对应的。

 

当θ值发生微小变化的时候，比如增加了dθ

圆弧也随之增加dθ。而y的值增加了看做d(sin(θ))

当我们去的dθ非常小的时候，dθ的值约等于下图中相似三角形的斜边的值。

我们用y值的变化d(sin(θ))/dθ，从图中的相似三角形可以看出，正好是邻边比斜边的，也就是cos(θ)

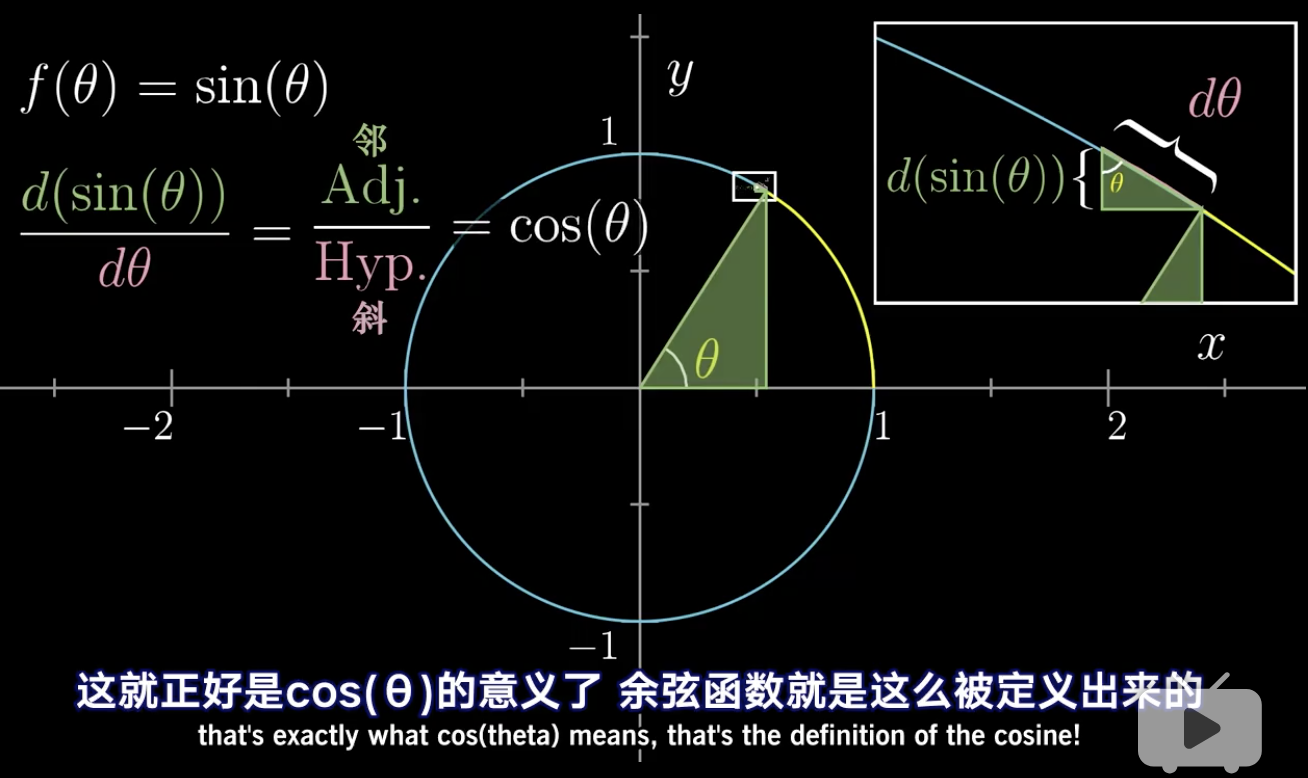
 很明显cos(θ)求导公式就是cos(θ)

那么你是否可以使用上面的方式证明一下。