01 微积分的本质 (2)

整理3Blue1Brown的课程内容，方便随时翻看。

原视频地址：https://www.bilibili.com/video/av10308208/

前文中，我们用一种先切分划分微小值的方式，将一个大问题划分为若干小问题，然后获得一个求得近似解的方法。

之后，我们通过将划分值不断缩小的方式，将原来的问题变成另外一个我们已经可以解决的问题。最后得到精确的结果。

通过这种方法，我们重新推导了计算圆的面积的公式。

现在我们看看这种方法在其他的地方如何发挥作用。

 

例如，已知骑车在每个时间点上的速度，求这段时间骑车走了多远的距离。

我们可以用每个时间点的速度乘以这段微小的时间，然后相加求和，就是这一整段时间走的距离的近似值。

从图中，我们可以看出，最后我们将一个物理学的问题，变成了几何学的问题。这是不是很有趣？

还有很多的问题都可以这样来计算，我们将一个复杂的问题，拆解为若干近似于a*b然后相加求和的问题(如上面的速度乘以时间)，

其中每一个乘法计算中的a都是相同的。（如上一例子中，每一个时间点之间的距离是相同的，也就是vt中的t是相同的）

那么我们就可以将问题转化为若干细长的矩形面积(a*b不就是求矩形面积的公式？)相加取得近似值的问题。

若是我们取的a（在这个汽车例子中的t）取值越小，我们最终获得的值就越精确，而且越发靠近求下图面积的问题的。

等等，这个形状的面积似乎也不是那么好求得。

似乎我们不会像求圆的面积的时候那么的幸运，得到图形正好是一个三角形。

如上题我们求一个汽车从发动到停止这段时间经过的距离，最后我们得到的这样一个形状，我们要怎么求它的面积呢？

一个二次函数的曲线下的面积要怎么求呢？

 

视频告诉我们，当你在数学上遇到一个特别难解的问题是，不要想着正面硬解，这样你往往会撞上南墙。

相反，你应该带着不明确的目的不断把玩这些概念。

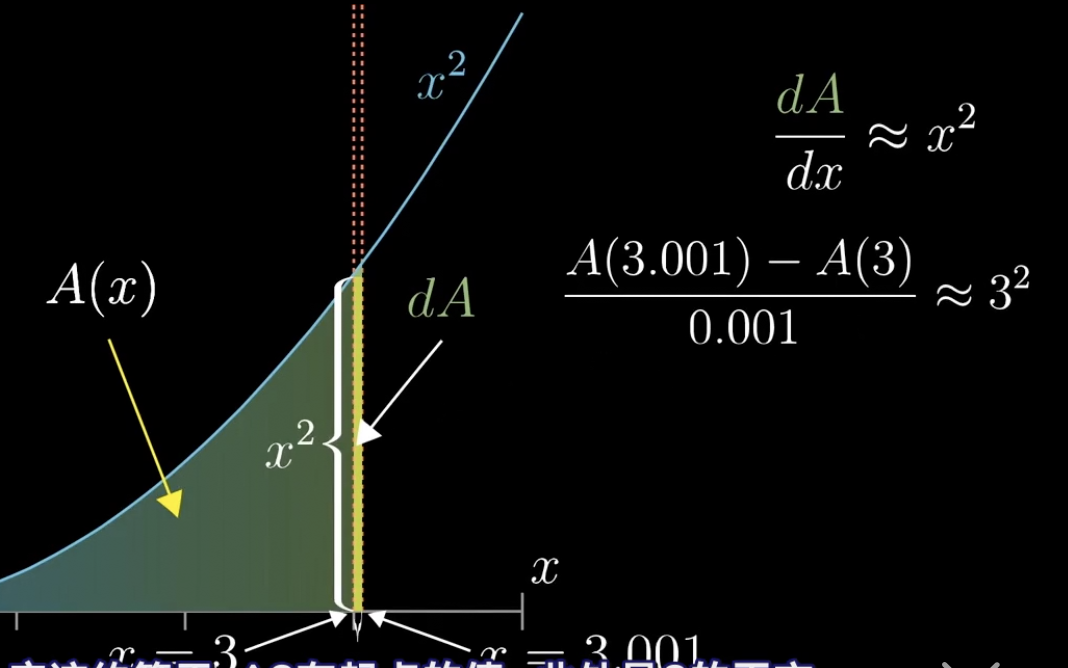
我们将二次函数，x²函数曲线下的面积设置A(x)

那么A(x)与x²之间有什么特殊关系呢？

如果我们将x的值增加一点点，那A(x²)的值回发生怎样的变化呢？

我们把增加的面积叫做dA，x的增加值叫做dx

我们将这个增加的面积近似看做一个矩形。

我们可以得到：

dA≈x²*dx   由此我们得到： dA/dx≈x²

这里我们dx的值取的越小，那么这个dA的面积就越接近矩形的面积。dA/dx也就越接近x²

我们将x=3,dx0.001代入这个公式可以得到

 

现在我们还是不知道神秘的A(x)，但是我们有了这样一个一个公式：dA/dx≈f(x)

dx取值越小，这个公式就越精确。