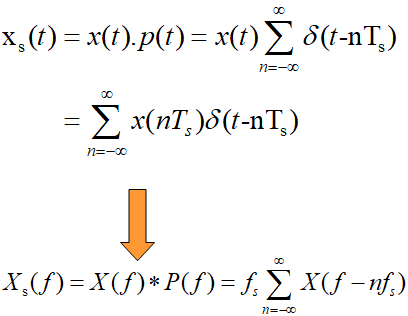FS,FT,DFS,DTFT,DFT,FFT的联系和区别
转自:https://www.cnblogs.com/WHaoL/p/6111528.html
1.Fourier变换的几种可能形式

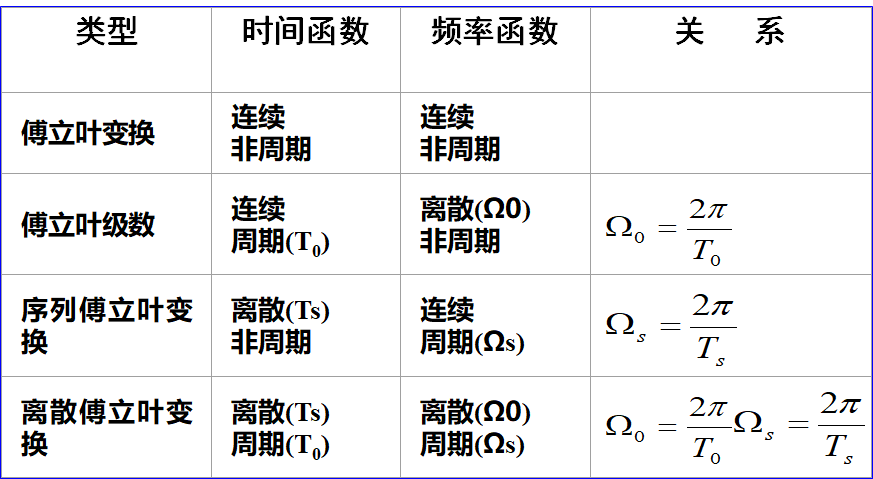
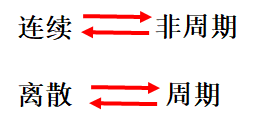
对应关系为:
![]()
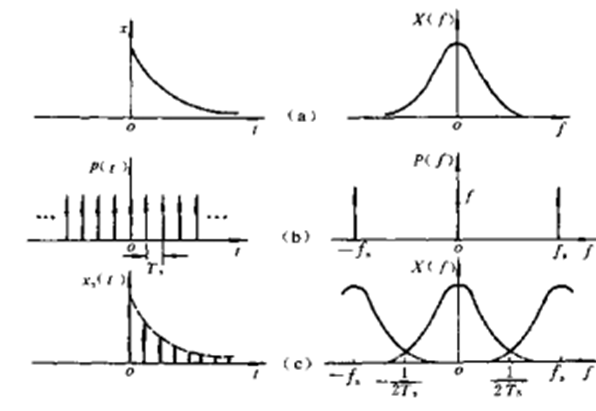
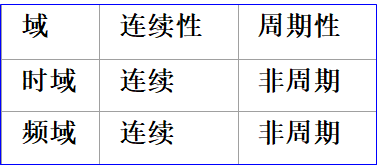
在自然界中除了存在温度,压力等在时间上连续的信号,还存在一些离散信号,离散信号可经过连续信号采样获得,也有本身就是离散的。例如,某地区的年降水量 或平均增长率等信号,这类信号的时间变量为年,不在整数时间点的信号是没有意义的。用于离散信号频谱分析的工具包括DFS,DTFT和DFT。
2.FS
FS(Fourier Series)傅里叶级数展开,它用于分析连续周期信号,时域上任意连续的周期信号可以分解为无限多个正弦信号之和,在频域上就表示为离散非周期的信号,即时域连续周期,对应频域离散非周期的特点。

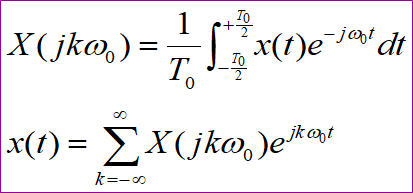


3.FT
FT(Fourier Transform)是傅里叶变换,它主要用于分析连续非周期信号,由于信号是非周期的,它必包含了各种频率的信号,所以具有时域连续非周期,对应频域连续非周期的特点。

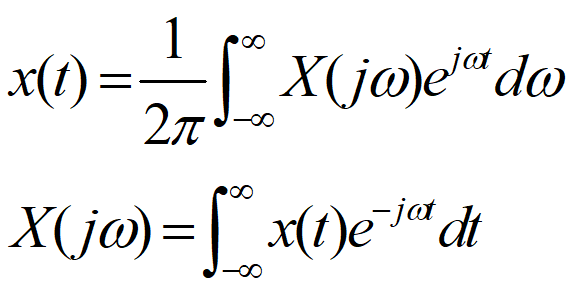

4.DTFT
DTFT(Discrete Time Fourier Transform)是离散时间傅里叶变换 ,它用于离散非周期序列分析,根据连续傅里叶变换要求连续信号在时间上必须可积这一充分必要条件,那么对于离散时间傅里叶变换,用于它之上的离散序列也必须满足在时间轴上级数求和收敛的条件;由于信号是非周期序列,它必包含了各种频率的信号,所以DTFT对离散非周期信号变换后的频谱为连续的,即有时域离散非周期,对应频域连续周期的特点。



当离散的信号为周期序列时,严格的讲,离散时间傅里叶变换是不存在的,因为它不满足信号序列绝对级数和收敛(绝对可和)这一傅里叶变换的充要条件,但是采用DFS这一分析工具仍然可以对其进行傅里叶分析。
5.DFS
DFS(Discrete Fourier Series)离散傅里叶级数,用于离散周期信号分析。我们知道周期离散信号是由无穷多相同的周期序列在时间轴上组成的,假设周期为N,即每个周期序列都有N个元素,而这样的周期序列有无穷多个,由于无穷多个周期序列都相同,所以可以只取其中一个周期就足以表示整个序列了,这个被抽出来表示整个序列特性的周期称为主值周期,这个序列称为主值序列。然后以N对应的频率作为基频构成傅里叶级数展开所需要的复指数序列ek(n)=exp(j*2pi*k*n/N),用主值序列与复指数序列取相关(乘加运算),得出每个主值在各频率上的频谱分量,这样就表示出了周期序列的频谱特性。DFS有时域离散周期,对应频域离散周期的特点。
根据DTFT,对于有限长序列作Z变换或序列傅里叶变换都是可行的,或者说,有限长序列的频域和复频域分析在理论上都已经解决;但对于数字系统,无论是Z 变换还是序列傅里叶变换的适用方面都存在一些问题,重要是因为频率变量的连续性性质(DTFT变换出连续频谱),不便于数字运算和储存。
6.DFT
DFT是为适应于数字计算机计算的傅里叶变换(FT),对于信号x(t)若要在计算机上实现傅里叶变换和傅里叶逆变换,需要做到:①把连续信号(包括时域和频域)都改为离散数据,②把计算范围收缩到一个有限的区间;③实现正,逆傅里叶变换。参考DFS,可以采用类似DFS的分析方法对解决以上问题。可以把有限长非周期序列假设为一无限长周期序列的一个主直周期,即对有限长非周期序列进行周期延拓,延拓后的序列完全可以采用DFS进行处理,即采用复指数基频序列和此有限长时间序列取相关,得出每个主值在各频率上的频谱分量以表示出这个“主值周期”的频谱信息。
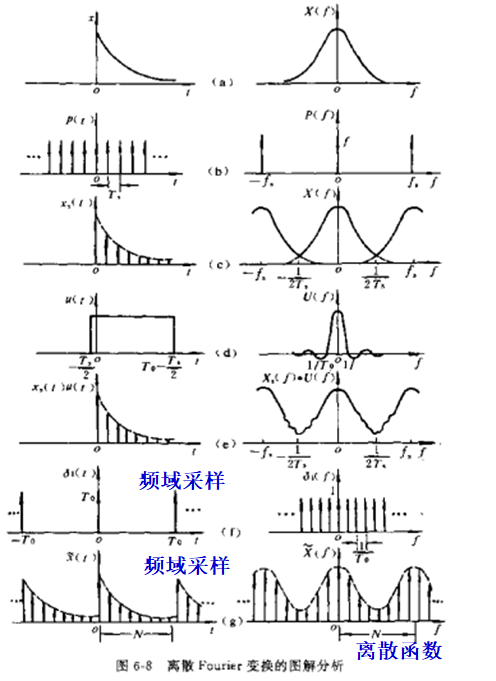
DFT(Discrete Fourier Transform)离散傅里叶变换,用于离散周期信号分析。由于DFT借用了DFS,这样就假设了序列的周期无限性,但在处理时又对区间作出限定(主值区间),以符合有限长的特点,这就使DFT带有了周期性。另 外,DFT只是对一周期内的有限个离散频率的表示,所以它在频率上是离散的,就相当于DTFT变换成连续频谱后再对其采样,此时采样频率等于序列延拓后的周期N,即主值序列的个数。(DFS是在时域上先采样后做FS变换,DFT是先在时域上采样,再FT变换,即DTFT变换,然后时域截断,最后再将DTFT变换后的连续频域上采样,即DFT对连续时间信号有三个过程:时域采样->时域截断->频域采样)
(1)时域采样
(2)时域截断
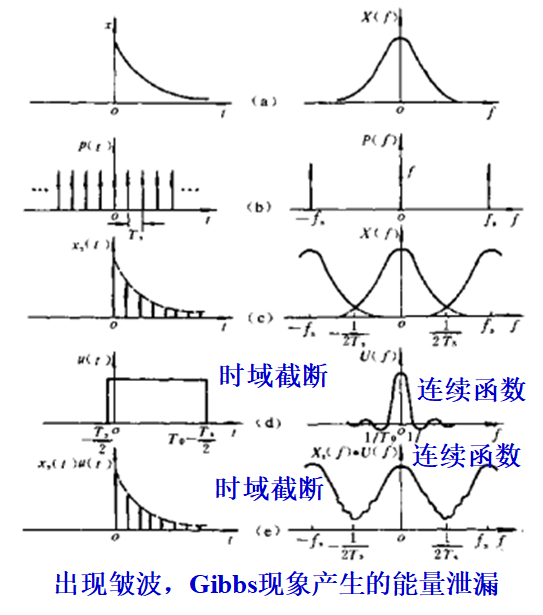

(3)频域采样
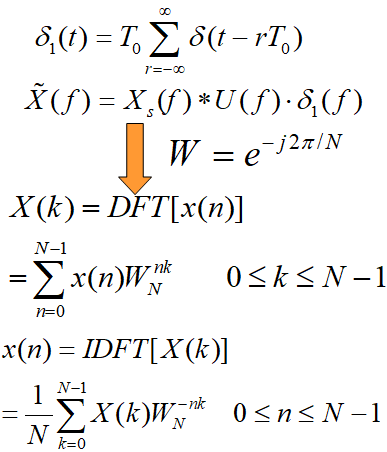
7.DFS,DTFT,DFT,FFT的联系与区别
下面谈谈DFS,DTFT,DFT,FFT的联系与区别
DFT与FFT其实是一个本质,FFT是DFT的一种快速算法。
DFS是discrete fourier seriers,对离散周期信号进行级数展开。DFT是将DFS取主值,DFS是DFT的周期延拓。计算上DFS是在时域上先采样后做FS变换,DFT是先在时域上采样,再FT变换,即DTFT变换,然后再将DTFT变换后的连续频域上采样。
DTFT是对Discrete time fourier transformation,是对序列的FT,是先在时域中采样,后傅里叶变换,得到连续的周期谱,而DFT,FFT得到是有限长的非周期离散谱,不是一个。
DFS、DTFT与FS、FT的差别在于,前两者都是先在时域上采样,然后进行FS和FT变换,便于计算机进行数字运算和存储。
DTFT与DFT的关系
我们知道,一个N点离散时间序列的傅里叶变换(DTFT)所的频谱是以(2*pi)为周期进行延拓的连续函数,由采样定理我们知道,时域进行采样,则频域周期延拓;同理,如果在频域进行采样,则时域也会周期延拓。离散傅里叶变换(DFT)就是基于这个理论,在频域进行采样,一个周期内采N个点(与序列点数相同) ,从而将信号的频谱离散化,得到一的重要的对应关系:一个N点离散时间信号可以用频域内一个N点序列来唯一确定,这就是DFT表达式所揭示的内容。
至于离散傅里叶变换DFT,其实也是对数字信号变换到频域进行分析处理,它对数字信号处理的作用相当大。数字信号处理脱离了模拟时期对信号进行处理完全依赖于器件的情况,可以直接通过计算来进行信号处理。如数字滤波器,只是用系统的系数对进入的数字信号进行一定的计算,信号出系统后即得到处理后的数据在时域 上的表达。
离散傅里叶变换在理解上与连续信号的傅里叶变换不太相同,主要是离散信号的傅里叶变换涉及到周期延拓,以及圆周卷积等。
快速傅里叶变换FFT其实是一种对离散傅里叶变换的快速算法,它的出现解决了离散傅里叶变换的计算量极大、不实用的问题,使离散傅里叶变换的计算量降低了 一个或几个数量级,从而使离散傅里叶变换得到了广泛应用。另外,FFT的出现也解决了相当多的计算问题,使得其它计算也可以通过FFT来解决。