整型并查集实现

并查集概念：

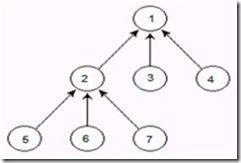
并查集是一种很有效对数据进行分类的数据结构，在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中，其特点是看似并不复杂，但数据量极大，若用正常的数据结构来描述的话，往往在空间上过大，计算机无法承受；即使在空间上勉强通过，运行的时间复杂度也极高，根本就不可能在比赛规定的运行时间（1～3秒）内计算出试题需要的结果，只能采用一种全新的抽象的特殊数据结构——并查集来描述。如图，就是一个并查集的结构：

 

 

并查集节点：

//使用数组表示，适用场合是固定大小的数组
struct Tree_node{
    int index;   //节点下标
    int parent;  //无父节点是为-1
    int value;   //节点值
    int rank;    //节点的秩
};
typedef struct Tree_node NODE;

NODE node[10]; //声明一个全局的数组

 

查找最高节点操作1：

//没有璐姐压缩的版本
int find_(NODE *n){
    int index = n->index;
    while(node[index].parent != -1){
        index = n->parent;
    }
    return index;
}

查找最高节点操作2：

//含有路径压缩的版本
int find(NODE *n){
    int final = find_(n); //先找到最终的父节点
    int index = n->index;
    while(node[index].parent != -1){
        node[index].parent = final;  //进行路径压缩
        index = node[index].parent;
    }
    return index;
}

 

并操作：

int union_(NODE *x,NODE *y){
    int final;
    int x_parent = find(x);
    int y_parent = find(y);
    if (node[x_parent].rank == node[y_parent].rank){
        node[y_parent].parent = x_parent;
        node[x_parent].rank += 1;
        final = x_parent;
    }else if(node[x_parent].rank > node[y_parent].rank){
        node[y_parent].parent = x_parent;
        final = x_parent;
    }else {
        node[x_parent].parent = y_parent;
        final = y_parent;
    }
    return final;
}

 

测试数据：

int main(){

    int i;
    int m1,m2,m0;
    m1 = m2 = m0 = 0;
    int p0[3];
    int p1[4];
    int p2[3];

    for(i=0;i<10;i++){
        node[i].index = i;
        node[i].parent = -1;
        node[i].rank = 0;
        node[i].value = i + 10;
        if(node[i].value % 3 == 0){
            p0[m0++] = i;
        }else if((node[i].value % 3 == 1)){
            p1[m1++] = i;
        }else{
            p2[m2++] = i;
        }
    }
   
    union_(&node[p0[0]],&node[p0[1]]);
    union_(&node[p0[2]],&node[p0[1]]);

    union_(&node[p1[0]],&node[p1[1]]);
    union_(&node[p1[2]],&node[p1[3]]);
    union_(&node[p1[2]],&node[p1[1]]);

    union_(&node[p2[0]],&node[p2[1]]);
    union_(&node[p2[2]],&node[p2[1]]);
   
    cout<<"ending is coming..";
    system("pause");
   
}