数据科学流程之维数约简
当数据集中包含大量特征时：
- 有些特征包含丰富的预测信息；
- 有些特征之间具有一定的相关性；
- 有些特征只包含噪声或不相关信息；
只保留有意义的特征不仅可以使数据集易于管理，而且可以使预测结果不受数据中噪声的影响，预测精度更好。
维数约简
消除输入数据集的某些特征，创建一个有限特征的数据集（包含所有需要的信息），以更有效的方式预测目标变量。
注：多维数组约简算法的一个主要假设：数据包含加性高斯白噪声。（加性高斯白噪声可以从我们的数据集中分离出来，它是一个线性噪声。）
ps：关于加性高斯白噪声指路博客：https://www.cnblogs.com/jiangkejie/p/10289876.html
维数约简可以减少噪声的集合跨度，以此减少噪声的能量。
一. 协方差矩阵
1. 协方差
协方差是对两个随机变量联合分布线性相关程度的一种度量。
- 两个随机变量越线性相关，协方差越大；
- 线性无关，协方差为零。
随机变量X,Y的协方差：
cov(X,Y) = E[(X-E[X])(Y-E[Y])]
cov(X,Y) = cov(Y,X) （协方差对称）
随机变量X与自身的协方差就是X的方差：
cov(X,X) = E[(X-E[X])(X-E[X])]
即
var(X) = cov(X,X) = E[(X-E[X])²]
2. 相关系数
相关系数（Correlation coefficient）是按积差方法计算，同样以两变量与各自平均值的离差为基础，通过两个离差相乘来反映两变量之间相关程度。
- 相关系数取值在-1到1之间；
- 相关系数为0时，称两个变量不相关；
- 相关系数为1时，称两个变量完全相关，即具有线性关系；
- 越接近于0说明两个变量的相似度越小；
- 越接近于1说明两个变量的相似度越大。
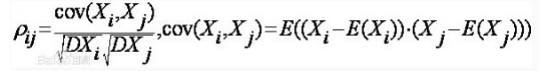
一般地，相关系数>0.8称为高度相关，相关系数<0.3称为低度相关，其他称为中度相关。
(一.2)
1 from sklearn.datasets import load_iris #载入鸢尾花数据 2 iris = load_iris() 3 print(iris.feature_names) 4 print(iris.data.shape)
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'] (150, 4)
1 import numpy as np 2 cov_data = np.cov(iris.data.T) 3 print(cov_data)
[[ 0.68569351 -0.042434 1.27431544 0.51627069] [-0.042434 0.18997942 -0.32965638 -0.12163937] [ 1.27431544 -0.32965638 3.11627785 1.2956094 ] [ 0.51627069 -0.12163937 1.2956094 0.58100626]]
1 import numpy as np 2 cov_data = np.corrcoef(iris.data.T) 3 print(cov_data)
[[ 1. -0.11756978 0.87175378 0.81794113] [-0.11756978 1. -0.4284401 -0.36612593] [ 0.87175378 -0.4284401 1. 0.96286543] [ 0.81794113 -0.36612593 0.96286543 1. ]]
输出矩阵的第一行第一个是数据集的'sepal length'和本身的协方差/相关系数；第一行第二个是数据集的'sepal length'和'sepal width'的协方差/相关系数；第二行第一个是数据集的
'sepal length'和'sepal width'的协方差/相关系数；第二行第三个是数据集的'sepal width'和'petal length'的协方差/相关系数。。。以此类推，所以会对称。
注：使用协方差矩阵和相关系数矩阵计算相关性的话，cov()和corrcoef()内输入数据必须每行是一个变量（特征），每列是一个样本，所以需要把数据进行转置。（具体算法参考例 一.2 ）
cov()/corrcoef()是协方差/相关系数矩阵，是对称矩阵，每个元素是各个向量元素之间的协方差/相关系数。
3. 热力图
矩阵图形化表示——heatmap() 热力图
1 import seaborn as sns #导入seaborn包和可视化绘图工具 2 import matplotlib.pyplot as plt 3 sns.heatmap(cov_data,annot = True)
1 sns.heatmap(cov_data,annot = True,cmap = 'rainbow')
参数annot(annotate标注的缩写)默认取值False;如果是True，在热力图每个方格写入矩阵对应位置数据。
参数cmap从数字到色彩空间的映射。
发现：
- 主对角线元素为1，因为变量自相关系数为1
- 第1和第3，第1和第4，第3和第4特征之间具有高度相关性；
- 第2特征与其他特征相关度较低。潜在特征量应该为2.
相关特征可能包含相似属性，因而可以约简高度相关特征。
维数约减算法很多，如PCA,LFA,LDA,LSA,ICA,T-SNE等。
二. 主成分分析
1.主成分分析
主成分分析（Principal component Analysis, PCA），又称主元分析，主分量分析，旨在利用降维的思想简化数据。
PCA的主要思想是通过对原始变量相关矩阵内部结构的关系研究，找出影响效果某一要素的几个综合指标，使综合指标为原来变量的线性拟合。
将n维特征映射到p维上，这p维是新的正交特征，被称为主成分。
p维特征是在原有m维特征的基础上重新构造出来的，不仅保留了原始变量的主要信息，且彼此间不相关，又比原始变量具有某些更优越的性质。 ——抓住主要矛盾
注：p维是从协方差矩阵上提取出来的，因而具有正交属性
2.PCA算法步骤
PCA（n_components=None, copy=True, whiten=False, svd_solver='full'）
参数：
n_components: 所要保留的主成分个数n，缺省时默认为None。赋值为int，如n_components=1,将把原始数据降到一个维度；赋值为string，如n_components='mle'，将自动选取特征个数n，使得满足所要求的方差百分比。
copy: 表示是否在运行时将原始训练数据复制一份，缺省时默认为True。若为True，则在原始数据副本上进行运算，原始数据不改变。若为False，则在运行PCA算法后，原始训练数据的值改变。
whiten: 白化，使得每个特征具有相同的方差，缺省时默认False。
svd_solver: 指定奇异值分解SVD的方法，缺省时默认auto。有四个可选择的值：{'auto','full','arpack','randomized'}
返回值：
n_components_: 返回所保留的成分个数n；
components_: 返回具有最大方差的成分；
explained_variancce_ratio_: 返回保留的n个成分各自的方差百分比。
2.1 特征分解
特征分解是奇异值分解的一个特例，一般PCA库都是基于SVD实现。
svd_solver参数：
指定奇异值分解SVD的方法：’auto‘,'full','arpack','randomized'
'full'：传统意义上的SVD，使用scipy库对应的SVD实现。
'randomized'和'arpack'：一般适用于数据量大，数据维度多，同时主城分数比例又较低的PCA降维，使用了加快SVD的随机算法。
区别：randomized使用scikit-learn的SVD实现；
arpack使用scipy库的sparse的SVD实现。
'auto'：PCA算法自行在前面三种中做权衡，选择一个合适的SVD算法来降维。
一般来说，使用默认值就够了。
2.2 Randomized PCA
scikit-learn提供了一种基于随机SVD（Randomized SVD）的更快的算法，它是一种更轻的，近似迭代分解的方法。
虽然使用随机SVD进行满秩重建并不十分理想，其基向量在每次迭代过程中会被局部优化，但是做矩阵分解时，随机SVD比经典SVD算法速度更快，只需要几个步骤就能与经典算法结果极其近似。因此，当训练数据集很大时，它是一个很好的选择。
当数据集的规模非常小时，Randomized PCA输出结果与经典PCA相当接近，但当这两种算法应用于大数据集时，其对比结果会显著不同。
1 from sklearn.decomposition import PCA 2 pca_2c = PCA(n_components=2)#初始化PCA，降为2维 3 X_pca_2c = pca_2c.fit_transform(iris.data)#把数据集里'data'部分进行标准化拟合,得到约简后的数据 4 X_pca_2c.shape
(150, 2)
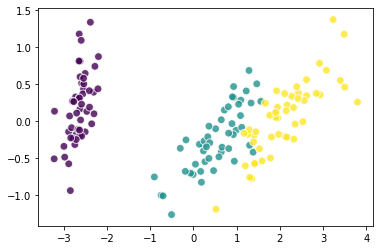
1 plt.scatter(X_pca_2c[:,0],X_pca_2c[:,1],c=iris.target,alpha=0.8,
s=60,marker='o',edgecolors='white') #plt.scatter参数x，y：表示的是大小为(n,)的数组，也就是我们即将绘制散点图的数据点；c:可以是'color'也可以是一个二维数组（一行的那种）；
alpha:0-1之间的实数；s:是一个实数或者是一个数组大小为(n,)，这个是一个可选的参数;marker:数据点的形状，默认为'o'（圆点）；
edgecolors:数据点边缘颜色
2 plt.show()
1 pca_2c.explained_variance_ratio_
array([0.92461872, 0.05306648])
pca_2c.explained_variance_ratio_.sum()
0.9776852063187949
pca_2c.components_
array([[ 0.36138659, -0.08452251, 0.85667061, 0.3582892 ],
[ 0.65658877, 0.73016143, -0.17337266, -0.07548102]])
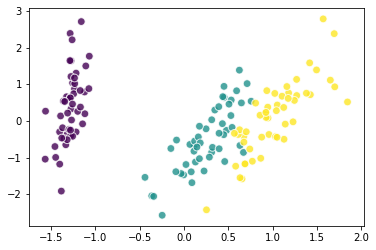
1 pca_2cw = PCA(n_components=2,whiten=True)#初始化PCA，降为2维并且白化 2 X_pca_2cw = pca_2cw.fit_transform(iris.data) 3 plt.scatter(X_pca_2cw[:,0],X_pca_2cw[:,1],c=iris.target,alpha=0.8, 4 s=60,marker='o',edgecolors='white') 5 plt.show()#数值范围变为2倍 6 pca_2cw.explained_variance_ratio_.sum()
0.9776852063187949
1 pca_1c = PCA(n_components=1)#初始化PCA，降为1维 2 X_pca_1c = pca_1c.fit_transform(iris.data) 3 plt.scatter(X_pca_1c[:,0],np.zeros(X_pca_1c.shape),c=iris.target,alpha=0.8, 4 s=60,marker='o',edgecolors='white') 5 plt.show() 6 pca_1c.explained_variance_ratio_.sum()
0.924618723201727
1 pca_95pc = PCA(n_components=0.95)#初始化PCA 2 X_pca_95pc = pca_95pc.fit_transform(iris.data) 3 print(pca_95pc.explained_variance_ratio_.sum()) 4 print(X_pca_95pc.shape)
0.9776852063187949 (150, 2)
