Leetcode数组类算法题1
1.
给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是,你不能重复利用这个数组中同样的元素。
示例:
给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]
使用count,返回的是被查找元素的个数。如果有,返回1;否则,返回0。注意,map中不存在相同元素,所以返回值只能是1或0。
使用find,返回的是被查找元素的位置,没有则返回map.end()。
//方法二:hashmap //关联容器是对容器概念的一个改进,将值与键关联在一起 //可以降低一重时间复杂度 class Solution { public: vector<int> twoSum(vector<int>& nums, int target) { unordered_map<int,int>m; vector<int>res; for (int i=0;i<nums.size();i++) { m[nums[i]]=i; } for (int j=0;j<nums.size();j++) { int t = target- nums[j]; if (m.count(t) && m[t]!=j){//判断的先后顺序一定不能弄错了 res.push_back(j); res.push_back(m[t]); break; } } return res; } };
11.
给定 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且 n 的值至少为 2。
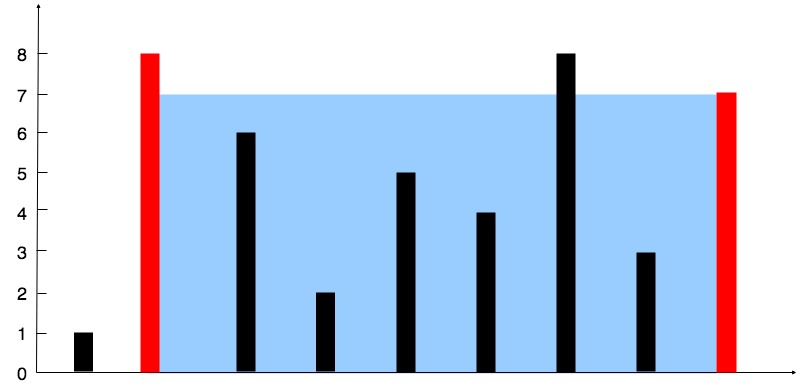
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例:
输入: [1,8,6,2,5,4,8,3,7]
输出: 49
//因为要求最大面积,所以游标从两边一起卡
class Solution { public: //这个时间复杂度只有O(n) //使用while循环,一定要找准那个让循环增加或者减少的那个点,非常重要。 //using namespace std; int maxArea(vector<int>& height) { int max = 0, i = 0, j = height.size() - 1; while (i < j) { max = std::max(max,std::min(height[i],height[j]) * (j - i)); if (height[i] < height[j]) i++; else j--; } return max; } }; //这种方法复杂度太大了,尽管结果通过了,能不暴力写就不要这样写 /* int maxArea(vector<int>& height) { int sum = 0;int sum1,sum2; for (int i=0;i<height.size();i++) { for(int j=i+1;j<height.size();j++) { sum1 = (j-i)*height[i]; sum2 = (j-i)*height[j]; if (height[j]>=height[i]&&sum1>=sum) sum = sum1; else if (height[j]<height[i]) { if (sum2>sum) sum = sum2; } } } return sum; }*/
15.
给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
例如, 给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为:
[
[-1, 0, 1],
[-1, -1, 2]
]
1.将数组排序
2.定义三个指针,i,j,k。遍历i,那么这个问题就可以转化为在i之后的数组中寻找nums[j]+nums[k]=-nums[i]这个问题,也就将三数之和问题转变为二数之和---(可以使用双指针)
//不能借鉴two sum的HashMap方法,就算用set去除重复也不好处理!
Python版本:
class Solution: def threeSum(self, nums: List[int]) -> List[List[int]]: nums.sort() res =[] i = 0 for i in range(len(nums)): if i == 0 or nums[i]>nums[i-1]: l = i+1 r = len(nums)-1 while l < r: s = nums[i] + nums[l] +nums[r] if s ==0: res.append([nums[i],nums[l],nums[r]]) l +=1 r -=1 while l < r and nums[l] == nums[l-1]: l += 1 while r > l and nums[r] == nums[r+1]: r -= 1 elif s>0: r -=1 else : l +=1 return res
C++版本1:(暴力计算肯定是超时的)
用双指针的方法
class Solution { public: vector<vector<int>> threeSum(vector<int>& nums) { vector<vector<int>> three;
vector<int>num; if (nums.size() >=3) { sort(nums.begin(), nums.end()); int first, last; for (int i = 0; i < nums.size() - 2; i++)//这是一个剪枝的过程,对第一个游标进行处理 { if (i>0 && nums[i] == nums[i - 1])
//后面这个判断是必须的,为什么呢?因为同样的数字只能处理一次!(当不需要两个数字同时用的时候)删掉会变成[[-1,-1,2],[-1,0,1],[-1,0,1]] continue; first = i + 1; last = nums.size() - 1; int sum; while (first != last)//用first和last两边游标同时逼近是减少时间复杂度的利器 { sum = nums[i] + nums[first] + nums[last]; if (sum < 0) first++; if (sum > 0) last--; if (sum == 0) { if (nums[first] != nums[first - 1]||first==i+1) { num.push_back(nums[i]); num.push_back(nums[first]); num.push_back(nums[last]); three.push_back(num); num.clear();//这一步非常重要! } first++; } } } } return three; } };
C++版本2:(有部分实例通不过,比如000的情况,继续思考)这种方法是模仿的two sum的方法!
//暴力计算的方法肯定是超时的! class Solution { public: vector<vector<int>> threeSum(vector<int>& nums) { vector<vector<int>>m; unordered_map<int,int> p; //至少要一重循环的 //vector<int>nums1=sort(nums); sort(nums.begin(),nums.end()); if (nums.size()>=3){ for (int i=0;i<nums.size();i++) { p[nums[i]]=i; } for (int i=0;i<nums.size()-2;i++) { if (i>0 && nums[i] == nums[i - 1]) continue; p[nums[i]]=i; vector<int>res; //这个前后可能有重复的,我怎么判断呢? for(int j=i+1;j<nums.size()-1;j++) { p[nums[j]]=j; int t = -nums[i]-nums[j]; //因为有两个-1,这个判断时候优先判断的是前面的一个 //if(p[t]<j) if (p.count(t) && p[t]>i && p[t]>j) { res.push_back(nums[i]);res.push_back(nums[j]);res.push_back(t); //break; m.push_back(res); res.clear(); } //m.push_back(res); } } } return m; } };
26.删除排序数组中的重复项
给定一个排序数组,你需要在原地删除重复出现的元素,使得每个元素只出现一次,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。
示例 1:
给定数组 nums = [1,1,2],
函数应该返回新的长度 2, 并且原数组 nums 的前两个元素被修改为 1, 2。
你不需要考虑数组中超出新长度后面的元素。
示例 2:
给定 nums = [0,0,1,1,1,2,2,3,3,4],
函数应该返回新的长度 5, 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。
你不需要考虑数组中超出新长度后面的元素。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以“引用”方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参做任何拷贝
int len = removeDuplicates(nums);
// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中该长度范围内的所有元素。
for (int i = 0; i < len; i++) {
print(nums[i]);
}
C++方法1:(这种方法没有原地修改数组)
class Solution { public: int removeDuplicates(vector<int>& nums) { vector<int>nums1; int len = nums.size(); //nums1[0] = nums[0]; //if (nums != NULL) if(nums.size()==0){ return 0; } nums1.push_back(nums[0]); for (int i=1;i<len;i++) { if(nums[i]!=nums[i-1]) nums1.push_back(nums[i]); } nums = nums1; return nums.size(); } };
C++方法2:(空间开销比前面一种小)
//用C++双指针的方法 class Solution { public: int removeDuplicates(vector<int>& nums) { int i=0,j=0; while(j<nums.size()) { int tmp = nums[j]; nums[i++] = nums[j++];//是相等过之后i和j分别+1 while(j<nums.size() && tmp == nums[j]) j++; } return i; } };
35. 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
你可以假设数组中无重复元素。
示例 1:
输入: [1,3,5,6], 5
输出: 2
示例 2:
输入: [1,3,5,6], 2
输出: 1
示例 3:
输入: [1,3,5,6], 7
输出: 4
示例 4:
输入: [1,3,5,6], 0
输出: 0
Python版本:(二分法查找)
class Solution(object): def searchInsert(self, nums, target): low = 0 high = len(nums) while low < high: mid = low + (high - low)/2 if nums[mid] > target: high = mid elif nums[mid] < target: low = mid +1 else: return mid return low
C++版本1:(这种题目非常简单)
class Solution { public: int searchInsert(vector<int>& nums, int target) { ////这个数组本来就排好序了 for(int i=0;i<nums.size();i++) { if(target==nums[i]) return i; else if (target<nums[i]) return i; //else // return nums.size(); else if (target>nums[nums.size()-1]) return nums.size(); } return 0; } };
C++版本2:(可以用lower_bound函数)
class Solution { public: int searchInsert(vector<int>& nums, int target) { int position = lower_bound(nums.begin(),nums.end(),target)-nums.begin(); return position; } };
C++版本3:常规方法----二分法
class Solution { public: int searchInsert(vector<int>& nums, int target) { int low = 0, high = nums.size();//二分法的high最好比最后一个数值位数大一个 int mid; while(low<high) { mid = low+(high-low)/2; if (nums[mid]>target) high = mid; else if (nums[mid]<target) low = mid + 1; else return mid; } return low; } };
53. 最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
进阶:
如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的分治法求解。
//要考虑全部是负数的情况
Python解法:
class Solution(object): def maxSubArray(self, nums): """ :type nums: List[int] :rtype: int """ for i in range(1, len(nums)): nums[i]= nums[i] + max(nums[i-1], 0) return max(nums)
C++解法一:(只要遍历两次)
class Solution { public: //找到一个具有最大和的连续子数组 int maxSubArray(vector<int>& nums) { int ans=0; int max=0; //这个负数的情况在这个函数里应该怎么处理? //if(max(nums)<0) // return std::max(nums);
//考虑全部是负数的情况 int max1=INT_MIN;//应该是数组的最小范围了 for(int i=0;i<nums.size();i++){ max1 = std::max(max1,nums[i]); } if (max1<0) return max1; for(int i=0;i<nums.size();i++) { ans+=nums[i]; if (ans<=0) ans=0; if (ans>max) max = ans; } return max; } };
C++解法二:(动态规划)
这道题根据题目关键词,“最大”“连续”,可以判断是一道动态规划,附上这道题目的wiki链接https://zh.wikipedia.org/wiki/%E6%9C%80%E5%A4%A7%E5%AD%90%E6%95%B0%E5%88%97%E9%97%AE%E9%A2%98 方法如下:
- 定义一个函数f(n),以第n个数为结束点的子数列的最大和,存在一个递推关系f(n) = max(f(n-1) + A[n], A[n]);
- 将这些最大和保存下来后,取最大的那个就是,最大子数组和。因为最大连续子数组 等价于 最大的以n个数为结束点的子数列和 附代码
class Solution { public: int maxSubArray(vector<int>& nums) { if(nums.size() == 0) return NULL; int res = INT_MIN; int f_n = -1; for(int i = 0; i < nums.size(); ++i){ f_n = max(nums[i], f_n + nums[i]); res = max(f_n, res); } return res; } };
66. 加一
给定一个由整数组成的非空数组所表示的非负整数,在该数的基础上加一。
最高位数字存放在数组的首位, 数组中每个元素只存储一个数字。
你可以假设除了整数 0 之外,这个整数不会以零开头。
示例 1:
输入: [1,2,3]
输出: [1,2,4]
解释: 输入数组表示数字 123。
示例 2:
输入: [4,3,2,1]
输出: [4,3,2,2]
解释: 输入数组表示数字 4321。
Python解法一:
(python 先通过list恢复成一个数 然后加1 再恢复成一个list)
class Solution(object): def plusOne(self, digits): """ :type digits: List[int] :rtype: List[int] """ value = 0 length = len(digits) for i in range(length): value += digits[length-i-1]*pow(10,i) value1 = value+1 res=[] while (value1 != 0): p = value1%10 value1 = value1/10 res.append(p) return list(reversed(res))
Python解法二:
class Solution(object): def plusOne(self, digits): """ :type digits: List[int] :rtype: List[int] """ return map(int, str(int(''.join(map(str,digits))) + 1))
C++ 解法:(活用insert函数)
class Solution { public: vector<int> plusOne(vector<int>& digits) { int carry = 1; for(int i = digits.size() - 1 ; i >= 0; i--){ int tmp = (digits[i] + carry) % 10; carry = (digits[i] + carry)/10; digits[i] = tmp; if(carry == 0)//因为这样,前面就不要动了,可以节省运行时间 break; } //这是判断最前面一个数字的情况 if(carry != 0) digits.insert(digits.begin(),1); return digits; } };
88.合并两个有序数组
给定两个有序整数数组 nums1 和 nums2,将 nums2 合并到 nums1 中,使得 num1 成为一个有序数组。
说明:
初始化 nums1 和 nums2 的元素数量分别为 m 和 n。
你可以假设 nums1 有足够的空间(空间大小大于或等于 m + n)来保存 nums2 中的元素。
示例:
输入:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6], n = 3
输出: [1,2,2,3,5,6]
(非常经典、常规的解法)
class Solution { public: void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) { int i1 = m - 1, i2 = n - 1; while(i1 >= 0 && i2 >= 0) { if(nums1[i1] > nums2[i2]) { nums1[i1 + i2 + 1] = nums1[i1]; i1--; } else { nums1[i1 + i2 + 1] = nums2[i2]; i2--; } } //如果是i1的话,多下来的话,直接用,位置不变 while(i2 >= 0) { nums1[i1 + i2 + 1] = nums2[i2]; i2--; } } };
118. 杨辉三角
给定一个非负整数 numRows,生成杨辉三角的前 numRows 行。

在杨辉三角中,每个数是它左上方和右上方的数的和。
示例:
输入: 5
输出:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
Python解法:
def generate(self, numRows): """ :type numRows: int :rtype: List[List[int]] """ result = [] for i in range(numRows): now = [1]*(i+1) if i >= 2: for n in range(1,i): now[n] = pre[n-1]+pre[n] result += [now] pre = now return result
C++ 解法:
如果单纯只是输出结果,确实不复杂,两个循环加上一个递归方法就能解决问题,代码也很优雅。但是提交的时候却没有通过,提示执行超时,显示的测试用例是输入数为30。仔细阅读了代码之后,做了2轮优化。1,递归是非常消耗资源的,仔细观察杨辉三角为对称结构,因此只需要递归其中一半的数据就可以,另外一半通过循环直接赋值;2,再仔细观察发现每一行的第二个和倒数第二个值为行数的值减一,这个特殊的地方可以直接返回计算值,而不需要递归计算,减少性能消耗。两次优化之后,终于提交成功
class Solution {//速度非常快,非常常规的思路! public: vector<vector<int>> generate(int numRows) { vector<vector<int>> vec(numRows); //相当于动态内存分配,相当于有numRows这么多的vector<int>结构 if(!numRows)
return vec; vec[0].push_back(1); if(numRows==1) return vec; vec[1].push_back(1); vec[1].push_back(1); if(numRows==2) return vec; for(int i=2;i!=numRows;++i) { vec[i].push_back(1); for(int j=0;j!=i-1;++j) {
vec[i].push_back(vec[i-1][j]+vec[i-1][j+1]);
} vec[i].push_back(1); } return vec; } };
119. 杨辉三角II
给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行。
在杨辉三角中,每个数是它左上方和右上方的数的和。
示例:
输入: 3
输出: [1,3,3,1]
进阶:
你可以优化你的算法到 O(k) 空间复杂度吗?
//当执行代码vector<int> v(2,5)时,在内存里建立了2个整形元素空间,值是5.
//assgin功能:将区间[first,last)的元素赋值到当前的vector容器中,或者赋n个值为x的元素到vector容器中,这个容器会清除掉vector容器中以前的内容。
C++ 解法1:(没有看懂)
class Solution { public: vector<int> getRow(int rowIndex) { vector<int> cur(1,1),pre; while(rowIndex--){ pre.assign(cur.begin(), cur.end()); cur.push_back(1); for(int i=1;i<cur.size()-1;i++) cur[i]=pre[i-1]+pre[i]; } return cur; } };
C++解法2:(用到了递归的思想)3=1+1+1 比较难想到
class Solution { public: vector<int> getRow(int rowIndex) { vector<int> rows(rowIndex + 1,1);//建立了这么多整型空间,值是1 for(int i = 0 ; i <= rowIndex; ++i){ for(int j = i - 1 ; j > 0 ; --j){ rows[j] += rows[j-1]; } } return rows; } };
121.买卖股票的最佳时机
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票),设计一个算法来计算你所能获取的最大利润。
注意你不能在买入股票前卖出股票。
示例 1:
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
示例 2:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
动态规划 前i天的最大收益 = max{前i-1天的最大收益,第i天的价格-前i-1天中的最小价格}
Python解法:
class Solution: def maxProfit(self, prices): """ :type prices: List[int] :rtype: int """ min_p, max_p = 999999, 0 for i in range(len(prices)): min_p = min(min_p, prices[i]) max_p = max(max_p, prices[i] - min_p) return max_p
C++ 解法:
(还是经典的dp思路)
class Solution { public: int maxProfit(vector <int>& prices) {
//简单动态规划方法
//这种不断用到前面结果的题目,用动态规划是一种好的方法 if(prices.size() <= 1) return 0; int min = prices[0], max = 0; for(int i = 1; i < prices.size(); i++) { max = std::max(max, prices[i] - min); min = std::min(min, prices[i]); } return max; } };
122. 买卖股票的最佳时机II
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
Python解法:
class Solution(object): def maxProfit(self, prices): profit = 0 for day in range(len(prices)-1): differ = prices[day+1] - prices[day] if differ > 0: profit += differ return profit
C++解法:(这道题目没有那么难,也不要想的太复杂了)
class Solution { public: int maxProfit(vector<int>& prices) { int res = 0; for (int i = 1; i < prices.size(); i++) if (prices[i] > prices[i - 1])
res += (prices[i] - prices[i - 1]); return res; } };
167. 两数之和 II - 输入有序数组
给定一个已按照升序排列 的有序数组,找到两个数使得它们相加之和等于目标数。
函数应该返回这两个下标值 index1 和 index2,其中 index1 必须小于 index2。
说明:
返回的下标值(index1 和 index2)不是从零开始的。
你可以假设每个输入只对应唯一的答案,而且你不可以重复使用相同的元素。
示例:
输入: numbers = [2, 7, 11, 15], target = 9
输出: [1,2]
解释: 2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。
C++解法:(指针对撞,减少开销)去用left和right比,可以减少一重循环
/*class Solution { public: //这个解法时间开销太大了 vector<int> twoSum(vector<int>& numbers, int target) { //int count = 0; vector<int>res(2); for (int i=0;i<numbers.size();i++) { for (int j=i+1;j<numbers.size();j++) { if(numbers[i]+numbers[j] == target) { //res.push_back(i+1); //res.push_back(j+1); res[0]=i+1; res[1]=j+1; break; //return res; } //break; } } return res; } };*/ //多用while循环,不要条件反射只会用for //第二种解法属于指针对撞的解法,可以降低时间复杂度,复杂度是O(n) //也可以用二分法,时间复杂度也是O(n) class Solution { public: vector<int> twoSum(vector<int>& numbers, int target) { vector<int> result; int left = 0, right = numbers.size() - 1; while(left < right){ if(numbers[left] + numbers[right] == target){ result.push_back(left + 1); result.push_back(right + 1); break; } else if(numbers[left] + numbers[right] > target){ right--; } else if(numbers[left] + numbers[right] < target){ left++; } } return result; } };
169. 求众数
给定一个大小为 n 的数组,找到其中的众数。众数是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在众数。
示例 1:
输入: [3,2,3]
输出: 3
示例 2:
输入: [2,2,1,1,1,2,2]
输出: 2
从第一个数开始count=1,遇到相同的就加1,遇到不同的就减1,减到0就重新换个数开始计数,总能找到最多的那个
C++解法1:
class Solution { public: int majorityElement(vector<int>& nums) { sort(nums.begin(),nums.end()); int i=0; int n=1; while(i<nums.size()-1) { while(i+1<nums.size() && nums[i+1]==nums[i]) { n++; i++; } if(n > (nums.size()/2)) return nums[i]; n=1; i++; } return nums[i]; } };
C++解法2:(自己写的,比较容易想)
class Solution { public: int majorityElement(vector<int>& nums) { sort(nums.begin(), nums.end()); int count = 1;//1 1 1 2 2 2 2 int i = 1; while(i<nums.size()) { if(nums[i]==nums[i-1]) { count++; if (count>nums.size()/2) return nums[i]; } else if (nums[i]!=nums[i-1]) { count=1; } i++; } return nums[0]; } };
209. 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的连续子数组。如果不存在符合条件的连续子数组,返回 0。
示例:
输入: s = 7, nums = [2,3,1,2,4,3]
输出: 2
解释: 子数组 [4,3] 是该条件下的长度最小的连续子数组。
进阶:
如果你已经完成了O(n) 时间复杂度的解法, 请尝试 O(n log n) 时间复杂度的解法。
//这种解法非常好!! class Solution { public: int minSubArrayLen(int s, vector<int>& nums) { int start=-1, minlength=nums.size()+1, sum=0; for (int i=0;i<nums.size();i++) { sum+=nums[i]; while (sum >= s) { minlength=min(minlength, i-start); start++; sum-=nums[start]; } } return minlength == nums.size()+1 ? 0 : minlength; } }; /* //这种解法也可以,比较容易理解!! class Solution { public: int minSubArrayLen(int s, vector<int>& nums) { int n = nums.size(); int sum = 0; int min = n + 1; for (int start = 0, end = 0; start < n && end < n;) { while (sum < s && end < n) sum += nums[end++]; while (sum >= s && start < n) { if (min > (end - start)) min = end - start; sum -= nums[start++]; } } if (min == (n + 1)) return 0; return min; } };*/
217. 存在重复元素
给定一个整数数组,判断是否存在重复元素。
如果任何值在数组中出现至少两次,函数返回 true。如果数组中每个元素都不相同,则返回 false。
示例 1:
输入: [1,2,3,1]
输出: true
示例 2:
输入: [1,2,3,4]
输出: false
示例 3:
输入: [1,1,1,3,3,4,3,2,4,2]
输出: true
Python解法:(直接用set)
class Solution: def containsDuplicate(self, nums): """ :type nums: List[int] :rtype: bool """ set1 = set(nums) if len(set1) == len(nums): return False else: return True
C++ 解法一:(用map去做,后面的键值存储出现了多少次)
class Solution { public: bool containsDuplicate(vector<int>& nums) { map<int,int> nums1;//一开始默认的初始值就是0 for(int i = 0;i<nums.size();i++) { nums1[nums[i]]++; if(nums1[nums[i]] == 2) return true; } return false; } };
C++解法二: (用set去做)
class Solution { public: bool containsDuplicate(vector<int>& nums) { set<int> s(nums.begin(),nums.end()); if(s.size() != nums.size()) return true; return false; } };
C++解法三:(最普通直接的解法,但是是最快的)
class Solution { public: bool containsDuplicate(vector<int>& nums) { if(nums.empty()) return false;
//注意判断空的情况 sort(nums.begin(),nums.end()); for(int i = 0;i<nums.size()-1;i++) { if(nums[i] == nums[i+1]) return true; } return false; } };
219. 存在重复元素II
给定一个整数数组和一个整数 k,判断数组中是否存在两个不同的索引 i 和 j,使得 nums [i] = nums [j],并且 i 和 j 的差的绝对值最大为 k。
示例 1:
输入: nums = [1,2,3,1], k = 3
输出: true
示例 2:
输入: nums = [1,0,1,1], k = 1
输出: true
示例 3:
输入: nums = [1,2,3,1,2,3], k = 2
输出: false
class Solution { public: //正常循环判断解法显示堆栈溢出,这是为什么呢? bool containsNearbyDuplicate(vector<int>& nums, int k) { unordered_map<int,int> m; for(int i=0;i<nums.size();i++) { if(m.count(nums[i]) && i-m[nums[i]]<=k) return true; m[nums[i]] = i; } return false; } };
414. 第三大的数
给定一个非空数组,返回此数组中第三大的数。如果不存在,则返回数组中最大的数。要求算法时间复杂度必须是O(n)。
示例 1:
输入: [3, 2, 1]
输出: 1
解释: 第三大的数是 1.
示例 2:
输入: [1, 2]
输出: 2
解释: 第三大的数不存在, 所以返回最大的数 2 .
示例 3:
输入: [2, 2, 3, 1]
输出: 1
解释: 注意,要求返回第三大的数,是指第三大且唯一出现的数。
存在两个值为2的数,它们都排第二。
Python解法:
class Solution: def thirdMax(self, nums: List[int]) -> int: nums = list(set(nums)) if len(nums) < 3: return max(nums) nums.sort(reverse=True) return nums[2]
C++解法:(用list和set的特性)---速度最好的方法
class Solution { public: int thirdMax(vector<int>& nums) { int small_fir=nums[0],small_sec=INT_MIN,i=1; long res=INT_MIN-1L; while(i<nums.size()&&nums[i]==small_fir) i++; if(i>=nums.size()) return small_fir; small_sec=nums[i]; if(small_fir<small_sec) swap(small_fir,small_sec); for(;i<nums.size();i++) { if(nums[i]<small_sec) res=max((long)nums[i],res); else if(nums[i]>small_fir) { res=small_sec; small_sec=small_fir; small_fir=nums[i]; } else if(nums[i]<small_fir&&nums[i]>small_sec) { res=small_sec; small_sec=nums[i]; } } return res==INT_MIN-1L?small_fir:(int)res; } };
448. 找到所有数组中消失的数字
给定一个范围在 1 ≤ a[i] ≤ n ( n = 数组大小 ) 的 整型数组,数组中的元素一些出现了两次,另一些只出现一次。
找到所有在 [1, n] 范围之间没有出现在数组中的数字。
您能在不使用额外空间且时间复杂度为O(n)的情况下完成这个任务吗? 你可以假定返回的数组不算在额外空间内。
示例:
输入:
[4,3,2,7,8,2,3,1]
输出:
[5,6]
【笔记】将所有正数作为数组下标,置对应数组值为负值。那么,仍为正数的位置即为(未出现过)消失的数字。
举个例子:
-
原始数组:[4,3,2,7,8,2,3,1]
-
重置后为:[-4,-3,-2,-7,
8,2,-3,-1]
结论:[8,2] 分别对应的index为[5,6](消失的数字)
class Solution { public: vector<int> findDisappearedNumbers(vector<int>& nums) { for (int i = 0; i < nums.size(); ++i) nums[abs(nums[i])-1] = -abs(nums[abs(nums[i])-1]); vector<int> res; for (int i = 0; i < nums.size(); ++i){ if (nums[i] > 0) res.push_back(i+1); } return res; } };
比较容易想,但是有差错,且使用了额外的空间
class Solution { public: vector<int> findDisappearedNumbers(vector<int>& nums) { sort(nums.begin(),nums.end()); vector<int>nums1; nums1.push_back(nums[0]); for(int i=1;i<nums.size();i++) { if(nums[i]!=nums[i-1]) nums1.push_back(nums[i]); else continue; } vector<int>nums2; for(int i=0;i<nums1.size();i++) { if(nums1[i+1]==nums1[i]+1) continue; else if (nums1[i+1]!=nums1[i]+1) //nums2.push_back(nums[i]+1); { int num = nums1[i+1]-nums1[i]; for(int j=1;j<num;j++) { nums2.push_back(nums1[i]+j); } } } return nums2; } };



