【第3章】微积分问题的计算机求解

极限问题的解析解

单变量函数的极限

假设已知函数f(x),则极限问题一般描述为

\[L=\lim_{x \to x_0} f(x) \]

此外，还有单边极限问题

\[L=\lim_{x \to x_0^-} f(x) \quad \text{左极限} \\ L=\lim_{x \to x_0^+} f(x) \quad \text{右极限} \]

matlab同样可以做这些极限运算

L=limit(fun,x,x0)    %求极限
L=limit(fun,x,x0,'left'或'right')    %求单边极限

举个例子

试求解极限问题

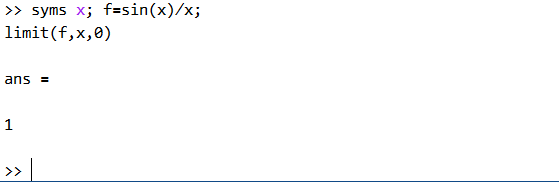
\[\lim_{x \to \infty} \frac{sin(x)}{x} \]

matlab代码

syms x; f=sin(x)/x; 
limit(f,x,0)

运行结果截图

多变量函数的极限

若想求出二元函数的极限

\[L=\lim_{x \to x_0 \atop y \to y_0} f(x) \]

我们可以嵌套使用limit()函数。

L1=limit(limit(f,x,x0),y,y0) 或
L1=limit(limit(f,y,y0),x,x0)

如果x0或y0不是确定的值，而是另一个变量的函数，例如 $ x \to g(y) $ ，则上述极限求取顺序不能交换。

函数导数的解析解

函数的导数和高阶导数

如果函数fun和自变量x都已知，且均为符号变量，则可以用diff()函数解出给定函数的各阶导数。

y=diff(fun,x)    %求导
y=diff(fun,x,n)  %求n阶导

例：给出如下函数，试求出其一阶导数

\[f(x)= \frac{sinx}{x^2+4x+3} \]

matlab代码

syms x;
f=sin(x)/(x^2+4*x+3);
f1=diff(f,x,1);
latex(f1)

最后得出结果如下

\[\frac{\cos\!\left(x\right)}{x^2 + 4\, x + 3} - \frac{\sin\!\left(x\right)\, \left(2\, x + 4\right)}{{\left(x^2 + 4\, x + 3\right)}^2} \]

复合泛函求导

例：给出如下函数，试求出其三阶导数公式，以及 $f(t)= e^{-t} $ 时的结果 关键 将f(t)声明为符号变量

\[F(t) = t^2 sint f(t) \]

matlab代码

syms t f(t); 
G=simplify(diff(t^2*sin(t)*f,t,3))
simplify(subs(G,f,exp(-t))), 
simplify(diff(t^2*sin(t)*exp(-t),3)-ans)

最后得出结果如下

G(t)=
6*cos(t)*f(t) + 6*sin(t)*diff(f(t), t) + 3*t^2*cos(t)*diff(f(t), t, t) + 12*t*cos(t)*diff(f(t), t) - 6*t*f(t)*sin(t) + t^2*sin(t)*diff(f(t), t, t, t) - 3*t^2*sin(t)*diff(f(t), t) + 6*t*sin(t)*diff(f(t), t, t) - t^2*cos(t)*f(t)

ans(t) =
2*exp(-t)*(3*cos(t) - 3*sin(t) + t^2*cos(t) + t^2*sin(t) - 6*t*cos(t))

ans(t) =
0

矩阵函数的求导

矩阵的求导：

\[H(x)= \begin{bmatrix} 4sin(5x) & e^{-4x^2} \\ 3x^2+4x+1 & \sqrt{4x^2+2} \\ \end{bmatrix} \]

可以对每个元素分别求导

syms x; 
H=[4*sin(5*x), exp(-4*x^2); 3*x^2+4*x+1, sqrt(4*x^2+2)];
H1=diff(H,x,3)

运行结果：

H1 =
 
[ -500*cos(5*x),                               192*x*exp(-4*x^2) - 512*x^3*exp(-4*x^2)]
[             0, (24*2^(1/2)*x^3)/(2*x^2 + 1)^(5/2) - (12*2^(1/2)*x)/(2*x^2 + 1)^(3/2)]

参数方程的导数

matlab中没有直接能够求解参数方程的函数，但我们可以根据其在数学上的定义来求：

根据递推公式，我们可以从中看出了，它的形式与我们之前学习的递归调用有很大的相似性，因此我们可以编写一个这样的函数paradiff(y,x,t,n)来求参数方程的n阶导数

%paradiff.m
function result=paradiff(y,x,t,n)
if mod(n,1)~=0, error('n should positive integer, please correct')
else, if n==1, result=diff(y,t)/diff(x,t);
   else, result=diff(paradiff(y,x,t,n-1),t)/diff(x,t);
end, end

例：已知参数方程如下，求其三阶导数

\[\begin{cases} y=\frac{sint}{(t+1)^3} \\ x=\frac{cost}{(t+1)^3} \end{cases} \]

matlab代码

syms t; 
y=sin(t)/(t+1)^3; 
x=cos(t)/(t+1)^3; 
f=paradiff(y,x,t,3); 
[n,d]=numden(f); %提取分子和分母，进行单独化简
F=simplify(n)/simplify(d)

运行结果

F =
(3*(t + 1)^7*(23*cos(t) + 24*sin(t) - 6*t^2*cos(t) - 4*t^3*cos(t) - t^4*cos(t) + 12*t^2*sin(t) + 4*t^3*sin(t) - 4*t*cos(t) + 32*t*sin(t)))/(3*cos(t) + sin(t) + t*sin(t))^5

多元函数的偏导数

matlab中没有求取偏导数的专门函数，但我们仍可以通过diff()函数直接实现。假设已知二元函数f(x,y),若想求

\[\frac{\partial ^{m+n}}{\partial x^m \partial y^n}f(x,y) \]

则可以使用下面的函数求出

f=diff(diff(f,x,m),y,n) %或者
f=diff(diff(f,y,n),x,m)

例：求如下函数的两个偏导数 $ \partial z / \partial x , \partial z / \partial y $

\[z=f(x,y)=(x^2-2x)e^{-x^2-y^2-xy} \]

matlab代码

syms x y; 
z=(x^2-2*x)*exp(-x^2-y^2-x*y); 
zx=simplify(diff(z,x)), 
zy=diff(z,y)

运行结果

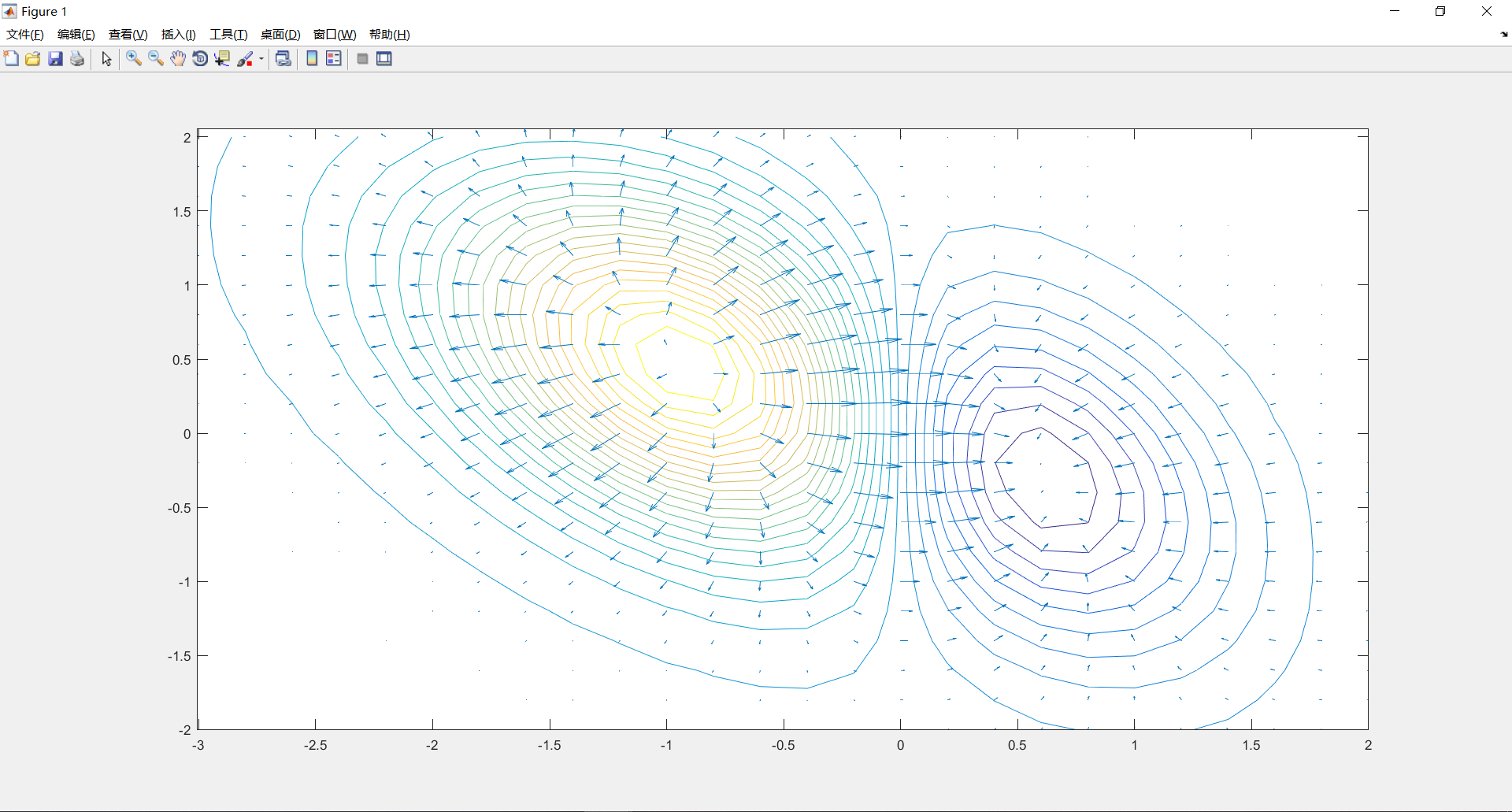
zx =
exp(- x^2 - x*y - y^2)*(2*x + 2*x*y - x^2*y + 4*x^2 - 2*x^3 - 2)
 
zy =
exp(- x^2 - x*y - y^2)*(- x^2 + 2*x)*(x + 2*y)

利用得到的偏导数函数zx，zy我们可以在z这个三维曲面上绘制出引力线，得到其梯度函数图形表示，引力线物理意义可看作一个小球在这个位置所受的力。

[x0,y0]=meshgrid(-3:.2:2,-2:.2:2); 
z0=double(subs(z,{x,y},{x0,y0})); %将符号型转为double型
surf(x0,y0,z0), zlim([-0.7 1.5]) %先画出Z曲面
contour(x0,y0,z0,30), hold on; %画出等高线并保持
zx0=subs(zx,{x,y},{x0,y0}); 
zy0=subs(zy,{x,y},{x0,y0}); %计算出各个点偏导数的值
quiver(x0,y0,-zx0,-zy0) %把偏导数结果用引力线形式表示出来

最终图如下：

隐函数的偏导数

还是直接上结论吧，matlab没有直接求隐函数的偏导数的函数，所以我们根据数学上的公式，编写函数impldiff(f,x,y,n)对 $ z=f(x,y) $ 求n阶偏导数

上代码：

%impldiff.m
function dy=impldiff(f,x,y,n)
if mod(n,1)~=0, error('n should positive integer, please correct')
else, F1=-simplify(diff(f,x)/diff(f,y)); dy=F1;
   for i=2:n, dy=simplify(diff(dy,x)+diff(dy,y)*F1); 
end, end   

例：求如下二元隐函数的一阶偏导数

\[z=f(x,y)=(x^2-2x)e^{-x^2-y^2-xy}=0 \]

matlab代码

syms x y; 
f=(x^2-2*x)*exp(-x^2-y^2-x*y); 
F1=impldiff(f,x,y,1)

运行结果：

F1 =
(2*x + 2*x*y - x^2*y + 4*x^2 - 2*x^3 - 2)/(x*(x + 2*y)*(x - 2))

多元函数的雅可比(Jacobian)矩阵

假设有n个自变量的m个函数定义为

\[\begin{cases} y_1=f_1(x_1,x_2,\cdots x_n) \\ y_2=f_2(x_1,x_2,\cdots x_n) \\ \qquad \quad \vdots \qquad \vdots \\ y_m=f_m(x_1,x_2,\cdots x_n) \end{cases} \]

将相应的 $ y_i $ 对 $ x_i $ 求偏导，则得出矩阵

\[J= \begin{bmatrix} \frac{\partial y_1 }{\partial x_1 } & \frac{\partial y_1 }{\partial x_2 } & \cdots & \frac{\partial y_1 }{\partial x_n } \\ \frac{\partial y_2 }{\partial x_2 } & \frac{\partial y_2 }{\partial x_2 } & \cdots & \frac{\partial y_2 }{\partial x_n } \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial y_m }{\partial x_1 } & \frac{\partial y_m }{\partial x_2 } & \cdots & \frac{\partial y_m }{\partial x_n } \end{bmatrix} \qquad \]

该矩阵又称为雅可比(Jacobian)矩阵,在matlab中可以用jacobian()函数直接求得。该函数的调用格式为jacobian(x,y)，其中x是自变量构成的向量，y是由各个函数构成的向量。

例：已知直角坐标和极坐标变换公式如下：

\[x=rsin\theta cos\phi ,y=rsin\theta sin\phi, z=rcos\theta \]

求雅可比矩阵

matlab代码

syms r theta phi; %三个自变量
x=r*sin(theta)*cos(phi); 
y=r*sin(theta)*sin(phi); 
z=r*cos(theta); %三个函数
J=jacobian([x; y; z],[r theta phi])

运行结果

J =
 
[ cos(phi)*sin(theta), r*cos(phi)*cos(theta), -r*sin(phi)*sin(theta)]
[ sin(phi)*sin(theta), r*cos(theta)*sin(phi),  r*cos(phi)*sin(theta)]
[          cos(theta),         -r*sin(theta),                      0]

积分运算

不定积分的求解

不定积分的形式

\[\int {f(x)}dx \quad \text{或者} \quad \int \cdots \int {f(x)}dx^n \]

matlab中用于计算积分的函数是int(fun,x)，其中fun为被积函数，x为积分变量。与求导数不同的是，当需要计算多重积分时，我们要使用嵌套的方式来计算多重积分。而且最终的到的结果是原函数，要在加常数C

\[F=int(\cdots int(fun,x)) \]

例：求如下函数的一阶导数在对结果求积分，与原函数比较

\[f(x)= \frac{sinx}{x^2+4x+3} \]

matlab代码

syms x; 
y=sin(x)/(x^2+4*x+3); 
y1=diff(y); 
y0=int(y1)

运行结果：

y0 =
 
sin(x)/(x^2 + 4*x + 3)

定积分与无穷积分的求解

\[\int_a^b {f(x)}dx \quad , \quad \int_a^\infty {f(x)dx} \]

matlab语句格式：

int(fun,x,a,b)
int(fun,x,a,inf)

还可以利用原函数计算

牛顿-莱布尼兹公式

\[\int_a^b {f(x)}dx =F(b)-F(a) \]

傅里叶(Fourier)级数逼近

给定周期函数 $ f(x), x \in[-L, L], T=2 L $ 可以人为的对该函数在其他区间上进行周期延拓，使得 $ f(x)=f(x+k T) $ ， k为任意整数，这样可以根据需要将其写成下面的级数形式

\[\begin{array}{c} f(x)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty}\left(a_{n} \cos \frac{n \pi}{L} x+b_{n} \sin \frac{n \pi}{L} x\right) \end{array} \]

其中，

\[\left\{\begin{array}{ll} a_{n} & =\frac{1}{L} \int_{-L}^{L} f(x) \cos \frac{n \pi x}{L} \mathrm{~d} x, \quad n=0,1,2, \cdots \\ b_{n} & =\frac{1}{L} \int_{-L}^{L} f(x) \sin \frac{n \pi x}{L} \mathrm{~d} x, \quad n=1,2,3, \cdots \end{array}\right. \]

该级数称为Fourier级数，而a_n，b_n又称为Fourier系数。若x∈(a，b)，则可以计算出L=(b-a)/2，引入新变量金，使得x=x+L+a，则可以将f(x)映射成(-L，L)区间上的函数，可对之进行Fourier级数展开，再将金=x-L-a转换成x的函数即可。MATLAB和Maple语言均未直提供求解Fourier系数与级数的现成函数。其实由上述公式不难编写出解析或数值的Fourier级数求解函数。其中解析函数如下：

%求Fourier级数展开的MATLAB代码 
%[F,A,B]=fseries(f,x,p,a,b)
function [F,A,B]=fseries(f,x,varargin)
[p,a,b]=default_vals({6,-pi,pi},varargin{:});
L=(b-a)/2; if a+b, f=subs(f,x,x+L+a); end
A=int(f,x,-L,L)/L; B=[]; F=A/2;
for n=1:p
   an=int(f*cos(n*pi*x/L),x,-L,L)/L; bn=int(f*sin(n*pi*x/L),x,-L,L)/L; 
    A=[A, an]; B=[B,bn]; F=F+an*cos(n*pi*x/L)+bn*sin(n*pi*x/L);
end
if a+b, F=subs(F,x,x-L-a); end

支持函数的编写

function varargout=default_vals(vals,varargin)
if nargout~=length(vals), error('number of arguments mismatch'); 
else, nn=length(varargin)+1;
    varargout=varargin; for i=nn:nargout, varargout{i}=vals{i};
end, end, end

该函数的调用格式为〔A，B，F]=fseries(f，x，p，a，b)，其中，f为给定函数，x为自
变量，p为展开项数，a，b为x的区间，可以省略取其默认值[-π，π]，得出的A，B为
Fourier系数，F为展开式。该函数应该置于@sym路径下。仿照解析解fseries(）函数
其实不难写出其数值版，有兴趣的读者可以自己试一试。

例：试求给定函数：$ x(x-π)(x-2π),x\in (0,2π) $ 的傅里叶级数展开

matlab代码：

syms x, y=x*(x-pi)*(x-2*pi);
F=fseries(y,x,12,0,2*pi);
F
%运行结果
F =

(3*sin(2*x))/2 + (4*sin(3*x))/9 + (3*sin(4*x))/16 + (12*sin(5*x))/125 + sin(6*x)/18 + (12*sin(7*x))/343 + (3*sin(8*x))/128 + (4*sin(9*x))/243 + (3*sin(10*x))/250 + (12*sin(11*x))/1331 + sin(12*x)/144 + 12*sin(x)

也就是这个：

\[f(x)= \sum _{n=1}^{\infty}\frac{12}{n^{3}}\sin nx \]

泰勒(Taylor)幂级数展开

单变量函数的泰勒幂级数展开

如果在x=0点处进行幂级数展开，那么有

\[f(x)=a_{1}+a_{2}x+a_{3}x^{2}+ \cdots +a_{k}x^{k-1}+o(x^{k}) \]

其中，系数$ a_i $可以由下面的公式求出来

\[a_i = \frac{1}{i!}\lim _{x \rightarrow 0}\frac{d^{i-1}}{dx^{i-1}}f(x),i=1,2,3\cdots \]

该幂级数展开又称为Maclaurin级数，若关于x=a点进行展开，则可以得出

\[f((x)=b_{1}+b_{2}(x-a)+b_{3}(x-a)^{2}+ \cdots +b_{k}(x-a)^{k-1}+o \left[(x-a)^{k}\right] \]

\[b_{i}= \frac{1}{i!}\lim _{x \rightarrow a}\frac{d^{i-1}}{dx^{i-1}}f(x),i=1,2,3\cdots \]

matlab解法：

%在x=0点处展开
F=taylor(fun,x,'Order',k)
F=taylor(fun,x, k) %早期matlab版本
%在x=a点处展开
F=taylor(fun,x,a,'Order', k)
F=taylor(fun,x,k,a) %早期matlab版本

例：求下列函数在x=0,x=a处的展开

\[f(x)= \frac{sinx}{x^{2}+4x+3} \]

syms x; f=sin(x)/(x^2+4*x+3); 
y=taylor(f,x,'Order',9)
syms a; taylor(f,x,a,'Order',5)

结果太长了我就不写了

多变量函数的泰勒幂级数展开

\[f(x)=f(a)+ \left[(x_{1}-a_{1})\frac{\partial}{\partial x_{1}}+ \cdots +(x_{n}-a_{n})\frac{\partial}{\partial x_{n}}\right] f(x)|_{x=a} \]

\[\frac{1}{2!}\left[(x_{1}-a_{1})\frac{\partial}{\partial x_{1}}+ \cdots +(x_{n}-a_{n})\frac{\partial}{\partial x_{n}}\right] ^{2}f(x)|_{x=a} + \cdots + \]

\[\frac{1}{k!}\left[(x_{1}-a_{1})\frac{\partial}{\partial x_{1}}+ \cdots +(x_{n}-a_{n})\frac{\partial}{\partial x_{n}}\right] ^{k}f(x)|_{x=a} + \cdots \]

matlab求法：

F=taylor(f,[x1,x2,···,xn],[a1,a2,···,an」,'Order',k)

例：二元函数

\[z=f(x,y)=(x^{2}-2x)e^{-x^{2}-y^{2}-xy} \]

1.在原点展开Taylor级数

symsxy；f=(x^2-2*x)*exp(-x^2-y^2-x*y)；
F=taylor(f,[x,y],[0,0],'Order’,8)；
collect(F,x)

2.关于(1,a)点展开

syms_a；
F=taylor(f,[x,y],[1,a],'Order’,3),
F1=simplify(F)

序列求和与序列求积运算