完全平方数

题目

给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, ...）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。

示例 1:

输入: n = 12
输出: 3 
解释: 12 = 4 + 4 + 4.

示例 2:

输入: n = 13
输出: 2
解释: 13 = 4 + 9.

 

题解

解法一:  BFS广度优先遍历

当每一次都可以判断出多种情况，有多次的时候就适合用BFS-广度优先遍历
使用BFS应注意：
队列：用来存储每一轮遍历得到的节点；
标记：对于遍历过的节点，应该将它标记，防止重复遍历。

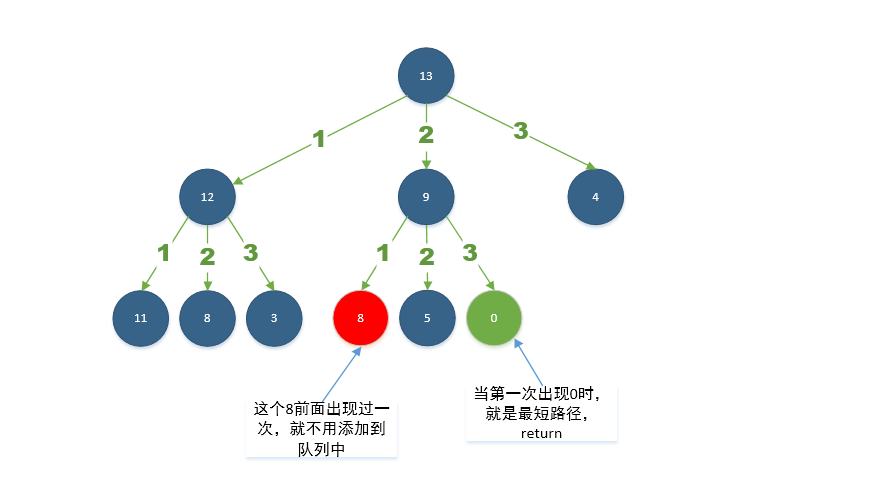
我们将它第一个平方数可能出现的情况做分析 只要 i * i < n 就行
再在此基础上进行二次可能出现的平方数分析
注意：为了节省遍历的时间，曾经（ n - 以前出现的平方数） 这个值出现过，则在此出现这样的数时直接忽略。

举个栗子：

 

 

public class Node {
        int val;
        int step;

        public Node(int val, int step) {
            this.val = val;
            this.step = step;
        }
    }


    public int numSquares(int n) {
        Queue<Node> queue = new LinkedList<>();
        queue.add(new Node(n, 1));
        boolean record[] = new boolean[n];
        while (!queue.isEmpty()) {
            int val = queue.peek().val;
            int step = queue.peek().step;
            queue.remove();
            // 每一层的广度遍历
            for (int i = 1;; i++) {
                int nextVal = val - i * i;
                // 说明已到最大平方数
                if (nextVal < 0)
                    break;

                // 由于是广度遍历，所以当遍历到0时，肯定是最短路径
                if(nextVal == 0)
                    return step;
                
                // 当再次出现时没有必要加入，因为在该节点的路径长度肯定不小于第一次出现的路径长
                if(!record[nextVal]){
                queue.add(new Node(nextVal,step + 1));
                record[nextVal] = true;
                }
            }
        }
        return -1;
    }

 

解法二: 动态规划

首先初始化长度为n+1的数组dp,每个位置都为0

如果n为0，则结果为0

对数组进行遍历，下标为i, 每次都将当前数字先更新为最大的结果，即dp[i]=i，比如i=4，最坏结果为4=1+1+1+1即为4个数字

动态转移方程为：dp[i] = MIN(dp[i], dp[i - j * j] + 1)，i表示当前数字，j*j表示平方数

时间复杂度：O(n*sqrt(n))，sqrt为平方根

public int numSquares(int n) {
    int[] dp = new int[n + 1]; // 默认初始化值都为0
    for (int i = 1; i <= n; i++) {
        dp[i] = i; // 最坏的情况就是每次+1
        for (int j = 1; i - j * j >= 0; j++) {
            dp[i] = Math.min(dp[i], dp[i - j * j] + 1); // 动态转移方程
        }
    }
    return dp[n];
}