二叉搜索树中第K小的元素-- 二分查找

题目

给定一个二叉搜索树，编写一个函数 kthSmallest 来查找其中第 k 个最小的元素。

说明：
你可以假设 k 总是有效的，1 ≤ k ≤ 二叉搜索树元素个数。

示例 1:

输入: root = [3,1,4,null,2], k = 1
   3
  / \
 1   4
  \
   2
输出: 1

示例 2:

输入: root = [5,3,6,2,4,null,null,1], k = 3
       5
      / \
     3   6
    / \
   2   4
  /
 1
输出: 3

进阶：
如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化 kthSmallest 函数？

 

前序

首先了解一下二叉搜索树.

二叉搜索树(Binary Search Tree)是指一颗空树或者具有下列性质的二叉树

• 任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

• 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

• 任意节点的左、右子树也分别为二叉查找树；

• 没有键值相等的节点。

二叉搜索树有一个有一个重要的性质, 中序遍历为排序数组,也就是从小到大排序

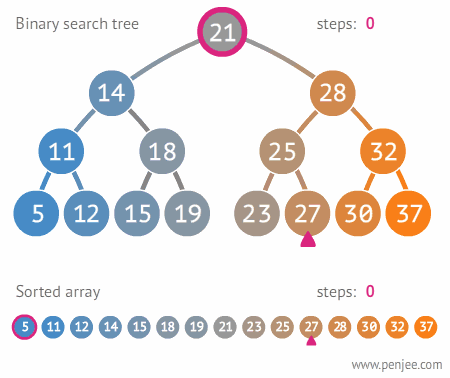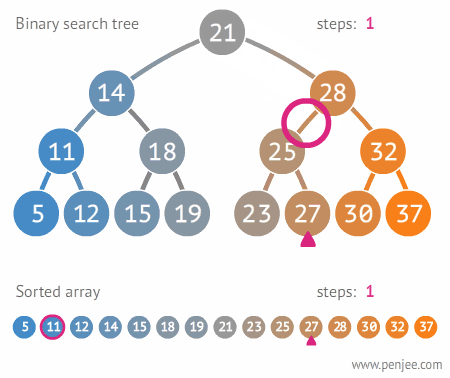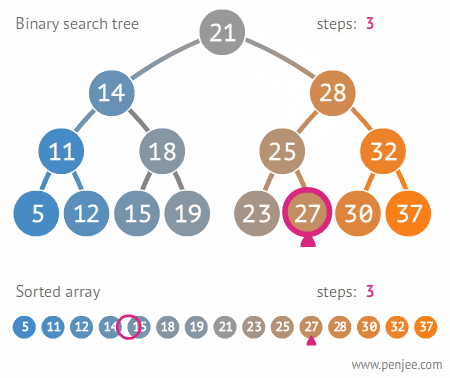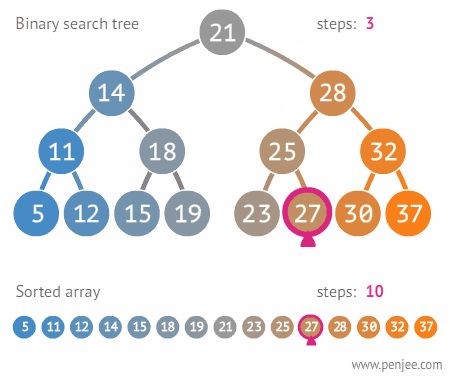
1. 查找 BST 中的某个元素

在二叉搜索树b中查找x的过程为：

1. 若b是空树，则搜索失败，否则：

2. 若x等于b的根节点的数据域之值，则查找成功；否则：

3. 若x小于b的根节点的数据域之值，则搜索左子树；否则：

4. 查找右子树。

2. 从有序数组构造一个二叉查找树

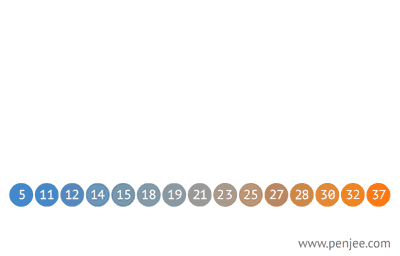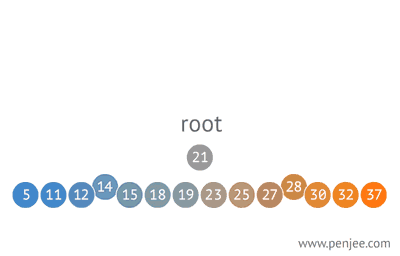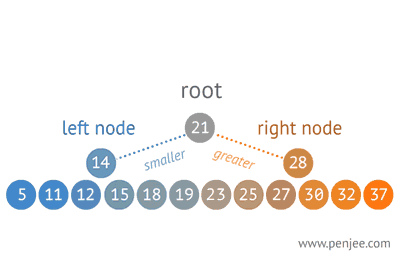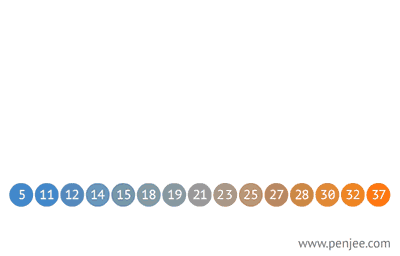
 3. 往 BST 中插入元素

向一个二叉搜索树b中插入一个节点s的算法，过程为：

1. 若b是空树，则将s所指结点作为根节点插入，否则：

2. 若s->data等于b的根节点的数据域之值，则返回，否则：

3. 若s->data小于b的根节点的数据域之值，则把s所指节点插入到左子树中，否则：

4. 把s所指节点插入到右子树中。（新插入节点总是叶子节点）

通过上面的前续,了解了二叉搜索树的基本内容和性质, 下面我们着重解决本题目!!!

思想 与 解法

1. 二分法

思想

二叉搜索树特点是左节点值小于根节点，而右节点值大于根节点；利用这个特性可以采用二分法，将整个树的节点分为左节点和右节点两部分，当k值等于左节点值+1时，说明此时root为要求的第k小元素；当k值小于左节点值时，说明第k小元素位于根节点左侧；当k值大于左节点时，说明第k小元素位于根节点右侧；之后递归，在满足条件的左右两侧节点中进行遍历划分，直到求出第k小。

代码

public class TreeNode {
    public var val: Int
    public var left: TreeNode?
    public var right: TreeNode?
    public init(_ val: Int){
        self.val = val
        self.left = nil
        self.right = nil
    }
}

func kthSmallest(_ root: TreeNode?, _ k: Int) -> Int {
    let left_num = calculate(root?.left)
    if k - 1 == left_num {
        return root?.val ?? 0
    } else if k - 1 < left_num {
        return kthSmallest(root?.left, k)
    } else {
        return kthSmallest(root?.right, k - 1 - left_num)
    }
}

func calculate(_ root: TreeNode?) -> Int {
    if root == nil {
        return 0
    }
    let num = 1 + calculate(root?.left) + calculate(root?.right)
    return num
}

 

2. 中序排序(递归)

二叉搜索树特点是左节点值小于根节点，而右节点值大于根节点；当我们进行中序遍历时【左中右】，就可以将整个二叉搜索树按照从小到大的顺序进行遍历，使用一个计数器，当与k值相等时，就可以输出当前节点元素。

public:
    int kthSmallest(TreeNode* root, int k) { //利用中序遍历进行计数
        int num = 0;
        int res = 0;
        Inorder(root,k,num,res);
        return res;
    }//中序遍历(左中右)
    void Inorder(TreeNode* root,int k,int &num,int &res){
        if(root == NULL)
        {
            return ;
        }
        Inorder(root->left,k,num,res);
        num++;
        if(k == num)
        {
            res = root->val;
        }
        Inorder(root->right,k,num,res);
    }

 

3. 中序排序(栈)

原理同样是中序遍历，但是结合了栈进行了操作，降低了递归引起的效率低的问题

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int kthSmallest(TreeNode *root, int k)
    {
        stack<TreeNode *> s;
        while (1)
        {
            if (root)
            {
                s.push(root);
                root = root->left;
                continue;
            }
            if (k == 1)
                return s.top()->val;
            root = s.top()->right;
            s.pop();
            k--;
        }
    }
};

 

以上就是二叉搜索树第k小元素的求解过程!!!