最长回文子串--动态规划

给定一个字符串s,找到s中最长的回文子串. 你可以假设 s 的最大长度为1000.

示例1

输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。

示例2

输入: "cbbd"
输出: "bb"

 

解法一: 暴力解法

根据回文子串的定义,枚举所有长度大于等于2的子串,以此判断它们是否是回文.在具体实现中,可以只针对大于“当前得到的最长回文子串长度”的子串进行回文子串.下面我们用暴力解法,列举出所有的,但是时间超出了限制,但是还是将这种方式贴出来

import Foundation //想要导入,否则string无subString方法
func longestPalindrome(_ s: String) -> String {
    guard s.count > 0 else {return ""}
    if s.count == 1 {return s}
    var maxLen: Int = 1
    
    let range = NSRange(location: 0, length: 1)
    let result = (s as NSString).substring(with: range)
    var resultStr = result as String
    
    for i in 0..<s.count - 1 {
        for j in i + 1..<s.count {
            if j - i + 1 > maxLen && valid(s, left1: i, right1: j) {
                maxLen = j - i + 1
                let range = NSRange(location: i, length: maxLen)
                let result = (s as NSString).substring(with: range)
                resultStr = result
            }
        }
    }
    return resultStr
}
//判断回文
func valid(_ s: String, left1: Int, right1: Int) -> Bool {
    let strArr = Array(s)
    var left: Int = left1
    var right: Int = right1
    while left < right {
        if strArr[left] != strArr[right]  {
            return false
        }
        left = left + 1
        right -= 1
    }
    return true
}

然后在leetCode上提交,但是时间超过了限制,给出的结果如下:

 

 

解法二: 动态规划

解法一的时间复杂度过高,在leetCode上并不能AC.下面有改进方法

首先我们定义P(i,j) 如下 

接下来

P( i , j ) = (P( i + 1,  j - 1 )&& S[ i ] == S[ j ])

所以如果我们知道了P( i, j )的情况,不需要调用判断回文串的函数了,只需要知道P( i + 1,  j - 1 )的情况就可以了,这样时间复杂度就会减少了O(n), 因此我们采取动态规划的方案,用空间换取时间,把已经求出来的P(i, j)存储起来.

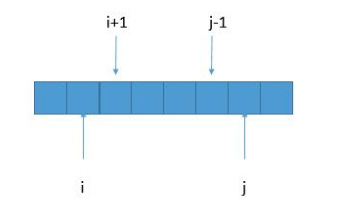
如果S[i + 1, j -1]是回文串, 那么只要S[i] == S[j] 就可以确定S[i, j]是回文串.

求长度为1和长度为2的P(i,j)时不能用上边的公式,因为带上去,发现越界,所以要分两种情况考虑.

所以我们先初始化长度为1的回文串的P(i,j),利用上面的提出的公式,然后两边向外各扩充一个字符,长度为3, 5的,所有的长度就求出来了.

同理, 初始化长度为2的回文串,利用公式,得到了长度为4, 6的所有偶数长度就都求出来了.

代码如下：

class Solution {
    public String longestPalindrome(String s) {
    int length = s.length();
    if (length == 1){return s;}
    boolean[][] P = new boolean[length][length];
    int maxLen = 0;
    String maxPal = "";
    for (int i = 1; i <= length; i++) //遍历所有的长度
    for (int j = 0; j < length; j++) {
        int k = i + j - 1;
        if (k >= length) //下标已经越界，结束本次循环
        break;
        P[j][k] = (i == 1 || i == 2 || P[j + 1][k - 1]) && s.charAt(j) == s.charAt(k); //长度为 1 和 2 的单独判断下
        if (P[j][k] && k > maxLen) {
            maxPal = s.substring(j, k + 1);
        }
    }
    return maxPal;
}
}

上面就是动态规划方法，还会持续更新，希望大家关注！！！