爬楼梯-动态规划

假设你正在爬楼梯.需要n阶你才能到达.

每次你可以爬1或者2个台阶.你有多少种不同的方法可以爬到楼顶呢?

注意: 给定n是一个正整数.

示例1:

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

示例2:

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

 

解法一: 动态规划

先不讲思想之类的,先看n值不断变化的时候,有什么规律吗?,用result记录多种可能性

1. 当n = 0 ,result = 0;
2. 当n = 1, result = 1;
3. 当n = 2, result = 2;
4. 当n = 3, result = 3;
5. 当n = 4, result = 5……

通过上面我们发现规律如下:

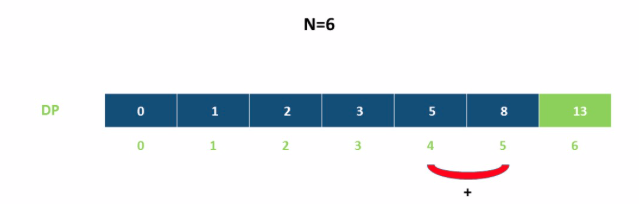
思想

下面我们谈思想,不难发现,这个问题可以被分解为一些包含最优子结构的子问题,即它的最优解可以从其子问题的最优解来有效的构建,可以用动态规划来解决这一问题.

第 i 阶可以由以下两种方法得到:

1. 在第(i - 1)阶后向上爬一阶
2. 在第(i - 2)阶后向上爬两阶

所以到达第 i 阶的方法总数就是第 (i - 1) 和第 (i - 2)阶的方法数之和.

令dp[ i ] 表示能到达第 i 阶的方法总数:

dp[ i ] = dp[i - 1] + dp[i - 2]

代码

func climbStairs(_ n: Int) -> Int {
        guard n > 0 else {return 0}
    if n == 1 {
        return 1
    }
    var dp: [Int] = [Int]()
    dp.append(0) //第一个元素,当n = 0,不存在方式爬到楼上
    dp.append(1) //第2个元素,当n = 1, 1种方式
    dp.append(2) //第3个元素,当n = 2, 2种方式
    for i in 3..<n + 1 {
        dp.append(dp[i - 1] + dp[i - 2]) //用append不如用=赋值
    }
    return dp[n]
    }

结果

上面就是动态规划的思想做,以后有其他思想做此题目,会更新最新的思想和代码(因本阶段专注动态规划解法).