python信用卡欺诈检测
信用卡欺诈检测
任务流程：
1、加载数据，观察问题
2、针对问题给出解决方案
3、数据集切分
4、评估方法对比
5、逻辑回归模型
6、建模结果分析
7、方案效果对比
读取数据
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
data = pd.read_csv("E:\python学习\回归\信用卡欺诈检测\creditcard.csv")
data.head()
| Time | V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | ... | V21 | V22 | V23 | V24 | V25 | V26 | V27 | V28 | Amount | Class | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | -1.359807 | -0.072781 | 2.536347 | 1.378155 | -0.338321 | 0.462388 | 0.239599 | 0.098698 | 0.363787 | ... | -0.018307 | 0.277838 | -0.110474 | 0.066928 | 0.128539 | -0.189115 | 0.133558 | -0.021053 | 149.62 | 0 |
| 1 | 0.0 | 1.191857 | 0.266151 | 0.166480 | 0.448154 | 0.060018 | -0.082361 | -0.078803 | 0.085102 | -0.255425 | ... | -0.225775 | -0.638672 | 0.101288 | -0.339846 | 0.167170 | 0.125895 | -0.008983 | 0.014724 | 2.69 | 0 |
| 2 | 1.0 | -1.358354 | -1.340163 | 1.773209 | 0.379780 | -0.503198 | 1.800499 | 0.791461 | 0.247676 | -1.514654 | ... | 0.247998 | 0.771679 | 0.909412 | -0.689281 | -0.327642 | -0.139097 | -0.055353 | -0.059752 | 378.66 | 0 |
| 3 | 1.0 | -0.966272 | -0.185226 | 1.792993 | -0.863291 | -0.010309 | 1.247203 | 0.237609 | 0.377436 | -1.387024 | ... | -0.108300 | 0.005274 | -0.190321 | -1.175575 | 0.647376 | -0.221929 | 0.062723 | 0.061458 | 123.50 | 0 |
| 4 | 2.0 | -1.158233 | 0.877737 | 1.548718 | 0.403034 | -0.407193 | 0.095921 | 0.592941 | -0.270533 | 0.817739 | ... | -0.009431 | 0.798278 | -0.137458 | 0.141267 | -0.206010 | 0.502292 | 0.219422 | 0.215153 | 69.99 | 0 |
5 rows × 31 columns
通过观察数据，发现第一列 time没有真实意义，其他V列的值比较匀称，但是Amount列值的波动比较大，我们希望的数据特征是数据波动比较稳定的。
##数据标签分布
count_classes = pd.value_counts(data['Class'],sort=True).sort_index()
print(count_classes)
# pandas画条形图
count_classes.plot(kind = 'bar')
plt.title("Fraud class histogram")
plt.xlabel("Class")
plt.ylabel("Frequency")
0 284315
1 492
Name: Class, dtype: int64
Text(0, 0.5, 'Frequency')
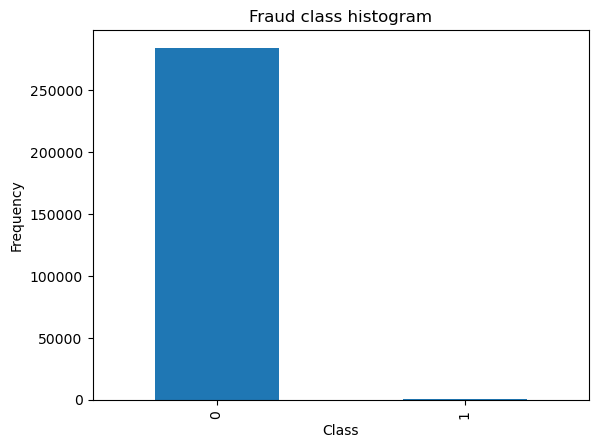
由于我们发现提供的数据集本身就很不规则，我们考虑对数据做进一步处理，主要2种思路：下采样和过采样。
# 引入sklearn 标准化处理模块
from sklearn.preprocessing import StandardScaler
data['normAmount'] = StandardScaler().fit_transform(data['Amount'].values.reshape(-1,1))
data = data.drop(['Time','Amount'],axis = 1)
data.head()
| V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 | V9 | V10 | ... | V21 | V22 | V23 | V24 | V25 | V26 | V27 | V28 | Class | normAmount | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -1.359807 | -0.072781 | 2.536347 | 1.378155 | -0.338321 | 0.462388 | 0.239599 | 0.098698 | 0.363787 | 0.090794 | ... | -0.018307 | 0.277838 | -0.110474 | 0.066928 | 0.128539 | -0.189115 | 0.133558 | -0.021053 | 0 | 0.244964 |
| 1 | 1.191857 | 0.266151 | 0.166480 | 0.448154 | 0.060018 | -0.082361 | -0.078803 | 0.085102 | -0.255425 | -0.166974 | ... | -0.225775 | -0.638672 | 0.101288 | -0.339846 | 0.167170 | 0.125895 | -0.008983 | 0.014724 | 0 | -0.342475 |
| 2 | -1.358354 | -1.340163 | 1.773209 | 0.379780 | -0.503198 | 1.800499 | 0.791461 | 0.247676 | -1.514654 | 0.207643 | ... | 0.247998 | 0.771679 | 0.909412 | -0.689281 | -0.327642 | -0.139097 | -0.055353 | -0.059752 | 0 | 1.160686 |
| 3 | -0.966272 | -0.185226 | 1.792993 | -0.863291 | -0.010309 | 1.247203 | 0.237609 | 0.377436 | -1.387024 | -0.054952 | ... | -0.108300 | 0.005274 | -0.190321 | -1.175575 | 0.647376 | -0.221929 | 0.062723 | 0.061458 | 0 | 0.140534 |
| 4 | -1.158233 | 0.877737 | 1.548718 | 0.403034 | -0.407193 | 0.095921 | 0.592941 | -0.270533 | 0.817739 | 0.753074 | ... | -0.009431 | 0.798278 | -0.137458 | 0.141267 | -0.206010 | 0.502292 | 0.219422 | 0.215153 | 0 | -0.073403 |
5 rows × 30 columns
第一种方式：采用下采样
X = data.iloc[:,data.columns != 'Class']
y = data.iloc[:,data.columns == 'Class']
number_records_fraud = len(data[data.Class==1]) ## class 为1 是异常值
fraud_indices = np.array(data[data.Class==1].index) ## 异常值数据的索引
normal_indices = data[data.Class==0].index ## 正常值数据的索引个数
# 对正常样本随即采用指定长度
random_normal_indices = np.random.choice(normal_indices,number_records_fraud,replace=False)
random_normal_indices = np.array(random_normal_indices)
# 合并新的索引项
under_sample_indices = np.concatenate([fraud_indices,random_normal_indices])
# 根据索引得到下采样的所有的样本点
under_sample_data = data.iloc[under_sample_indices,:]
X_undersample = under_sample_data.iloc[:,under_sample_data.columns!='Class']
y_undersample = under_sample_data.iloc[:,under_sample_data.columns=='Class']
#打印比例
print("正常样本比例:",len(under_sample_data[under_sample_data.Class==0])/len(under_sample_data))
print("异常样本比例:",len(under_sample_data[under_sample_data.Class==1])/len(under_sample_data))
print("下采样的总样本:",len(under_sample_data))
正常样本比例: 0.5
异常样本比例: 0.5
下采样的总样本: 984
数据集划分 这里我们需要注意的是，数据集划分成 训练集 和 测试集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=0)
print("原始训练集包含样本:",len(X_train))
print("原始测试集包含样本数量:",len(X_test))
print("原始样本总数:",len(X_train)+len(X_test))
# 对下采样的数据集进行划分
X_train_undersample,X_test_undersample,y_train_undersample,y_test_undersample = train_test_split(X_undersample,y_undersample,test_size=0.3,random_state=0)
print("下采样训练集包含样本:",len(X_train_undersample))
print("下采样测试集包含样本数量:",len(X_test_undersample))
print("下采样总数:",len(X_train_undersample)+len(X_test_undersample))
原始训练集包含样本: 199364
原始测试集包含样本数量: 85443
原始样本总数: 284807
下采样训练集包含样本: 688
下采样测试集包含样本数量: 296
下采样总数: 984
### 选择模型评估方法
准确率：分类问题中做对的占总体的百分比
召回率：正例中有多少能够预测，覆盖面的大小，比如我们看异常次数，那么假设总共异常值 10次，我们预测到是异常的是 6次， 那么召回率就是 0.6
精确度，被分为正例中实际为正例的比例
## Recall = TP / (TP + FN)
from sklearn.model_selection import KFold,cross_val_score,cross_val_predict
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import recall_score,confusion_matrix
def printing_Kfold_scores(x_train_data,y_train_data):
fold = KFold(n_splits=5,shuffle=False)
c_param_range = [0.01,0.1,1,10,100] # 定义不同力度的正则化惩罚力度
## 展示结果用的表格
result_table = pd.DataFrame(index = range(len(c_param_range),2),columns=['C_parameter','Mean recall score'])
result_table['C_parameter'] = c_param_range
# k - fold 表示 K折交叉验证，这会得到2个索引集， 训练集 indices[0] 验证集 indices[1]
j = 0
## 循环遍历不同的惩罚力度
for c_param in c_param_range:
print('----------------------')
print('正则化惩罚力度' , c_param)
print('----------------------')
print('')
recall_accs = []
## 一步步分解来做交叉验证 把训练集数据 重新分成 新的训练集和验证集
for iteration,indices in enumerate(fold.split(x_train_data),start=1):
## 指定算法模型，并给定参数
Ir = LogisticRegression(C = c_param, penalty='l2')
## 训练模型，注意训练的时候，一定传入的训练集，所以 x 和 y 的索引都是 0
Ir.fit(x_train_data.iloc[indices[0],:],y_train_data.iloc[indices[0],:].values.ravel())
## 进行模型预测，这时候用的是 验证集 索引 为 1
y_pred_undersample = Ir.predict(x_train_data.iloc[indices[1],:].values)
## 有了预测结果之后，就可以进行模型评估，这里 recall_score 需要传入 预测值和真实值
recall_acc = recall_score(y_train_data.iloc[indices[1],:].values,y_pred_undersample)
recall_accs.append(recall_acc)
print('Iteration',iteration,':召回率 = ',recall_accs[-1])
## 当执行完所有的交叉验证后，计算平均结果
result_table.loc[j,'Mean recall score'] = np.mean(recall_accs)
j += 1
print()
print("平均召回率:",np.mean(recall_accs))
print()
best_c = result_table.iloc[result_table['Mean recall score'].astype('float32').idxmax()]['C_parameter']
print(">>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>")
print('效果最好的模型选择的参数=',best_c)
print(">>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>")
return best_c
## 交叉验证与不同参数的结果
best_c = printing_Kfold_scores(X_train_undersample,y_train_undersample)
----------------------
正则化惩罚力度 0.01
----------------------
Iteration 1 :召回率 = 0.821917808219178
Iteration 2 :召回率 = 0.8493150684931506
Iteration 3 :召回率 = 0.8983050847457628
Iteration 4 :召回率 = 0.9324324324324325
Iteration 5 :召回率 = 0.8787878787878788
平均召回率: 0.8761516545356806
----------------------
正则化惩罚力度 0.1
----------------------
Iteration 1 :召回率 = 0.863013698630137
Iteration 2 :召回率 = 0.863013698630137
Iteration 3 :召回率 = 0.9661016949152542
Iteration 4 :召回率 = 0.9459459459459459
Iteration 5 :召回率 = 0.8939393939393939
平均召回率: 0.9064028864121736
----------------------
正则化惩罚力度 1
----------------------
Iteration 1 :召回率 = 0.863013698630137
Iteration 2 :召回率 = 0.8767123287671232
Iteration 3 :召回率 = 0.9830508474576272
Iteration 4 :召回率 = 0.9324324324324325
Iteration 5 :召回率 = 0.9242424242424242
平均召回率: 0.9158903463059488
----------------------
正则化惩罚力度 10
----------------------
Iteration 1 :召回率 = 0.863013698630137
Iteration 2 :召回率 = 0.8767123287671232
Iteration 3 :召回率 = 0.9830508474576272
Iteration 4 :召回率 = 0.9459459459459459
Iteration 5 :召回率 = 0.9393939393939394
平均召回率: 0.9216233520389545
----------------------
正则化惩罚力度 100
----------------------
Iteration 1 :召回率 = 0.863013698630137
Iteration 2 :召回率 = 0.8767123287671232
Iteration 3 :召回率 = 0.9830508474576272
Iteration 4 :召回率 = 0.9459459459459459
Iteration 5 :召回率 = 0.9393939393939394
平均召回率: 0.9216233520389545
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
效果最好的模型选择的参数= 10.0
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
混淆矩阵
from sklearn.metrics import confusion_matrix
from itertools import product as product
def plot_confusion_matrix(cm,classes,title='Confusion matrix',cmap=plt.cm.Blues):
plt.imshow(cm,interpolation='nearest',cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks,classes,rotation=0)
plt.yticks(tick_marks,classes)
thresh = cm.max() / 2.
for i, j in product(range(cm.shape[0]),range(cm.shape[1])):
plt.text(j,i,cm[i,j],
horizontalalignment="center",
color="white" if cm[i,j] > thresh else "black")
plt.tight_layout()
plt.ylabel("True label")
plt.xlabel("Predicted label")
下采样模型 应用于下采样数据
Ir = LogisticRegression(C=best_c,penalty='l2')
Ir.fit(X_train_undersample,y_train_undersample.values.ravel())
y_pred_undersample = Ir.predict(X_test_undersample.values)
cnf_matrix = confusion_matrix(y_test_undersample,y_pred_undersample)
np.set_printoptions(precision=2)
print("模型应用于下采样的召回率：",cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix,
classes=class_names,
title='Confusion matrix')
plt.show()
模型应用于下采样的召回率： 0.9183673469387755
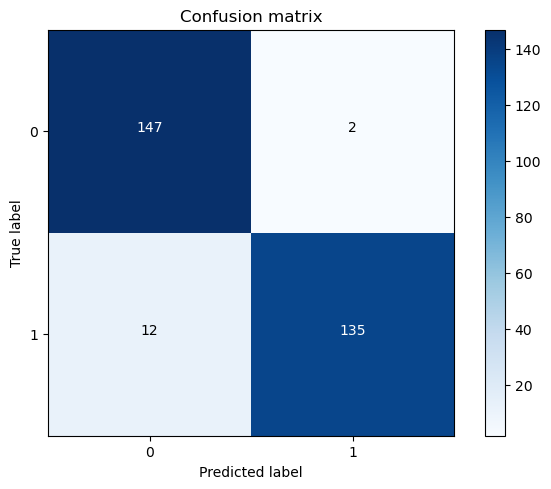
下采样模型应用于原始数据
Ir = LogisticRegression(C=best_c,penalty='l2')
Ir.fit(X_train_undersample,y_train_undersample.values.ravel())
y_pred = Ir.predict(X_test.values)
cnf_matrix = confusion_matrix(y_test,y_pred)
np.set_printoptions(precision=2)
print("下采样模型应用于原始数据的召回率：",cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix,
classes=class_names,
title='Confusion matrix')
plt.show()
下采样模型应用于原始数据的召回率： 0.9319727891156463
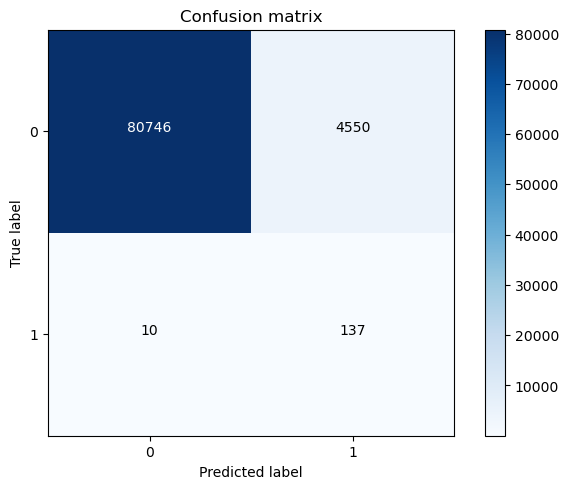
不同阈值影响
Ir = LogisticRegression(C=best_c,penalty='l2')
Ir.fit(X_train_undersample,y_train_undersample.values.ravel())
y_pred_undersample_proba = Ir.predict_proba(X_test_undersample.values)
thresholds = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]
plt.figure(figsize=(10,10))
j = 1
for i in thresholds:
y_test_predictions_high_recall = y_pred_undersample_proba[:,1] > i
plt.subplot(3,3,j)
j+=1
cnf_matrix = confusion_matrix(y_test_undersample,y_test_predictions_high_recall)
np.set_printoptions(precision=2)
print("Recall metric in the testing dataset: ", cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
class_names = [0,1]
plot_confusion_matrix(cnf_matrix,
classes=class_names,
title="Threshold >= %s"%i)
Recall metric in the testing dataset: 0.9659863945578231
Recall metric in the testing dataset: 0.9387755102040817
Recall metric in the testing dataset: 0.9319727891156463
Recall metric in the testing dataset: 0.9251700680272109
Recall metric in the testing dataset: 0.9183673469387755
Recall metric in the testing dataset: 0.9183673469387755
Recall metric in the testing dataset: 0.8775510204081632
Recall metric in the testing dataset: 0.8639455782312925
Recall metric in the testing dataset: 0.8571428571428571
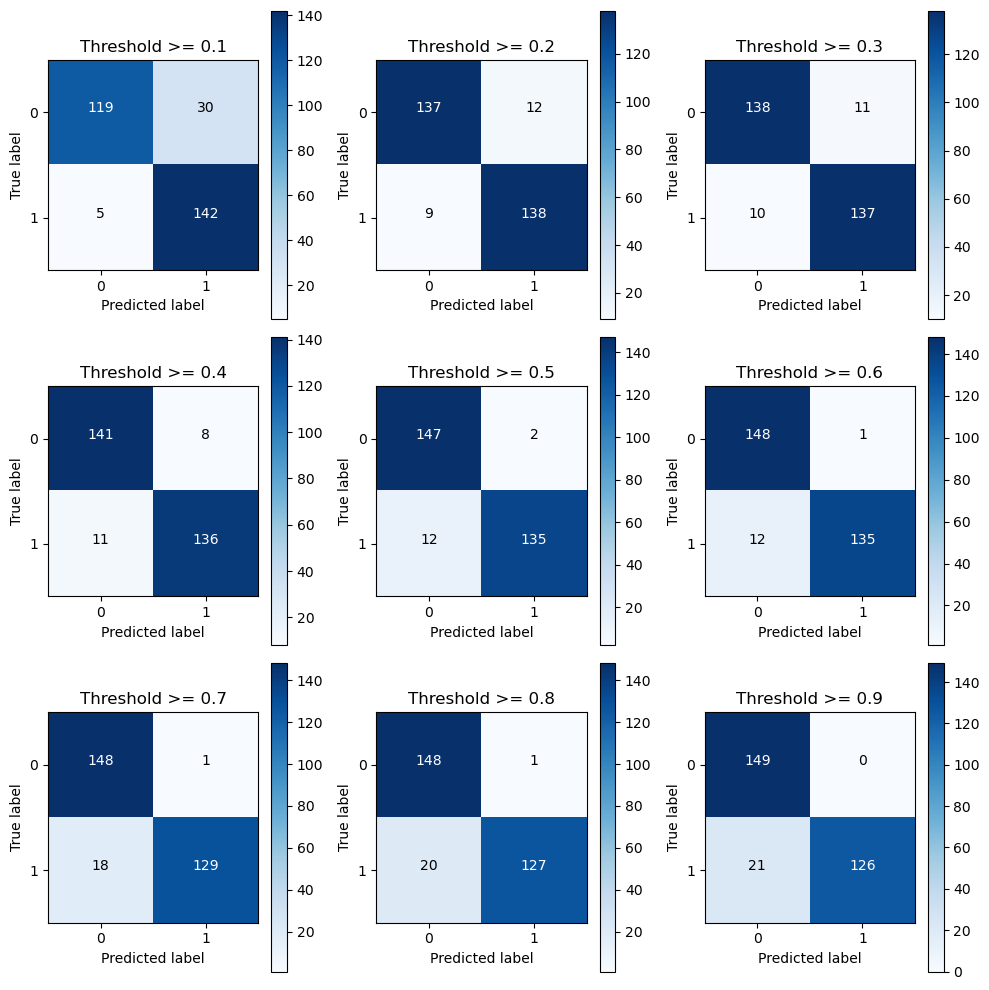
第二种方式 过采样方案
# 过采样， 使用 smote算法生成样本
# 引入逻辑回归模型
# 加载数据
data = pd.read_csv("E:\python学习\回归\信用卡欺诈检测\creditcard.csv")
# Amount特征值太大，进行正规化
data['normAmount'] = StandardScaler().fit_transform(data['Amount'].values.reshape(-1, 1))
# 删除无用的Time列和原 Amount列
data = data.drop(['Time', 'Amount'], axis=1)
# 获取特征列,所有行，列名不是Class的列
features = data.loc[:, data.columns != 'Class']
# 获取标签列，所有行，列名是Class的列
labels = data.loc[:, data.columns == 'Class']
# 分离训练集和测试集
features_train, features_test, labels_train, labels_test = train_test_split(features, labels, test_size=0.2, random_state=0)
from imblearn.over_sampling import SMOTE
oversampler = SMOTE(random_state=0)
os_features,os_labels=oversampler.fit_resample(features_train,labels_train)
os_features = pd.DataFrame(os_features)
os_labels = pd.DataFrame(os_labels)
best_c = printing_Kfold_scores(os_features,os_labels)
----------------------
正则化惩罚力度 0.01
----------------------
Iteration 1 :召回率 = 0.9161290322580645
Iteration 2 :召回率 = 0.9144736842105263
Iteration 3 :召回率 = 0.9105676662609273
Iteration 4 :召回率 = 0.8931754981809389
Iteration 5 :召回率 = 0.893626141721898
平均召回率: 0.905594404526471
----------------------
正则化惩罚力度 0.1
----------------------
Iteration 1 :召回率 = 0.9161290322580645
Iteration 2 :召回率 = 0.9144736842105263
Iteration 3 :召回率 = 0.9115857032200951
Iteration 4 :召回率 = 0.8943295852980293
Iteration 5 :召回率 = 0.895120959321177
平均召回率: 0.9063277928615785
----------------------
正则化惩罚力度 1
----------------------
Iteration 1 :召回率 = 0.9161290322580645
Iteration 2 :召回率 = 0.9144736842105263
Iteration 3 :召回率 = 0.911807015602523
Iteration 4 :召回率 = 0.8945384201096932
Iteration 5 :召回率 = 0.8952528549917016
平均召回率: 0.9064402014345017
----------------------
正则化惩罚力度 10
----------------------
Iteration 1 :召回率 = 0.9161290322580645
Iteration 2 :召回率 = 0.9144736842105263
Iteration 3 :召回率 = 0.9118734093172512
Iteration 4 :召回率 = 0.8945713940273244
Iteration 5 :召回率 = 0.8952528549917016
平均召回率: 0.9064600749609737
----------------------
正则化惩罚力度 100
----------------------
Iteration 1 :召回率 = 0.9161290322580645
Iteration 2 :召回率 = 0.9144736842105263
Iteration 3 :召回率 = 0.9118734093172512
Iteration 4 :召回率 = 0.8945713940273244
Iteration 5 :召回率 = 0.8952638462975786
平均召回率: 0.906462273222149
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
效果最好的模型选择的参数= 100.0
>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
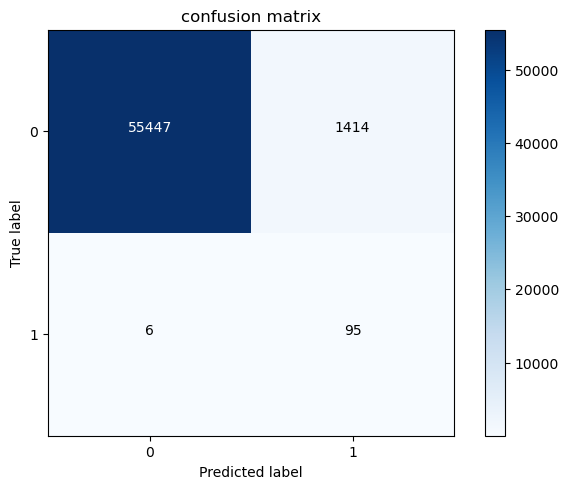
#### 过采样模型 应用于 过采样数据
Ir = LogisticRegression(C=best_c,penalty='l2')
Ir.fit(os_features,os_labels.values.ravel())
y_pred = Ir.predict(features_test.values)
cnf_matrix = confusion_matrix(labels_test,y_pred)
np.set_printoptions(precision=2)
print("过采样混淆矩阵：",cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix,
classes=class_names,
title="confusion matrix")
plt.show()
过采样混淆矩阵： 0.9405940594059405
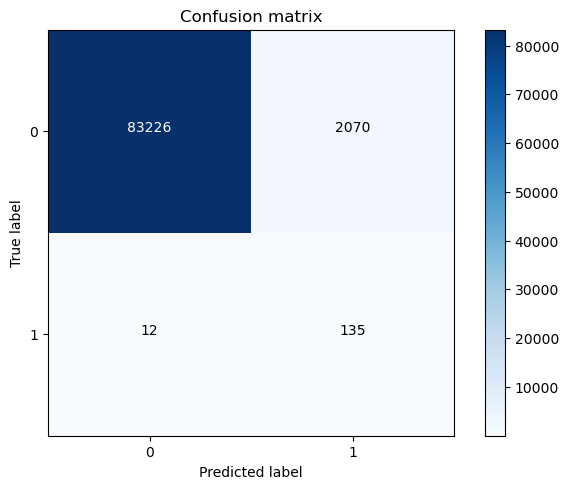
#### 过采样模型 应用于 真实数据
Ir = LogisticRegression(C=best_c,penalty='l2')
Ir.fit(os_features,os_labels.values.ravel())
y_pred = Ir.predict(X_test.values)
cnf_matrix = confusion_matrix(y_test,y_pred)
np.set_printoptions(precision=2)
print("过采样模型应用于原始数据的召回率：",cnf_matrix[1,1]/(cnf_matrix[1,0]+cnf_matrix[1,1]))
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix,
classes=class_names,
title='Confusion matrix')
plt.show()
过采样模型应用于原始数据的召回率： 0.9183673469387755
