朴素贝叶斯算法小结
朴素贝叶斯naive bayes是直接生成方法,也就是直接找出特征输出Y和特征X的联合分布P(X,Y)P(X,Y),然后用P(Y|X)=P(X,Y)/P(X)P(Y|X)=P(X,Y)/P(X)得出。
朴素贝叶斯算法是基于贝叶斯定理与特征条件独立假设的分类方法
这里提到的贝叶斯定理、特征条件独立假设就是朴素贝叶斯的两个重要的理论基础。
1. 数学基础:
1.1贝叶斯定理(条件概率公式)

1.2.朴素 -- 样本的特征之间独立(特征条件独立假设)
1.3.联合概率
联合概率是指在多元的概率分布中多个随机变量分别满足各自条件的概率。表示两个事件共同发生的概率。A与B的联合概率表示为 P(AB) 或者P(A,B),或者P(A∩B)
1.4.概率论的链式法则
2个事件同时发生的概率:
P(a, b) = P(a | b) * P(b) 其中:P(a, b)表示 a和b事件同时发生的概率, P(a | b)是一个条件概率,表示在b事件发生的条件下,a发生的概率
P(X1, X2, ... Xn) = P(X1 | X2, X3 ... Xn) * P(X2 | X3, X4 ... Xn) ... P(Xn-1 | Xn) * P(Xn)
1.5. 概率分布,是指用于表述随机变量取值的概率规律
(在贝叶斯算法中,P(x|k)表示类别k里特征x出现的概率,最大问题是如果数据集太少,那么从数据集里计算出来的概率偏差将非常严重,所以使用概率分布来计算概率,不是从数据集中来计算概率)
概率密度函数:连续型随机变量在某个特定值的可能性
概率质量函数:离散型随机变量在某个特定值的可能性
伯努利分布 Bernoulli Distribution,亦称“零一分布”、“两点分布”:一个事情有两种可能的结果,其中结果为1的发生概率为a,结果2发生的概率为1-a
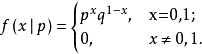
二项分布 Binomial Distribution :重复n次独立的伯努利试验,某个结果出现次数的概率
多项分布 Multinomial Distribution:多次进行满足类别分布的实验中,所有类别出现次数组合的分布。
多项分布是对二项分布的扩展,二项分布是单变量分布,而多项分布是多变量分布。二项分布的典型例子是抛硬币,每次试验有正反两种对立的可能,多项分布的例子是扔骰子,每次试验有多种可能,进行多次试验,多项分布描述的是每种可能发生次数的联合概率分布
某随机实验如果有k个可能结局A1、A2、…、Ak,分别将他们的出现次数记为随机变量X1、X2、…、Xk,它们的概率分布分别是p1,p2,…,pk,那么在n次采样的总结果中,A1出现n1次、A2出现n2次、…、Ak出现nk次的这种事件的出现概率P有下面公式:

高斯分布 Gaussian Distribution/Normal Distribution :正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人们又经常称之为钟形曲线
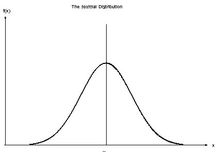
正态分布有两个参数,即期望(均数)μ和标准差σ,σ2为方差。(μ为样本的平均值,其决定了高斯分布的位置,σ为标准差,其决定了高斯分布的幅度,σ越大,分布越分散,σ越小,分布越集中)
正态分布公式:
2.朴素贝叶斯-推导
https://blog.csdn.net/u012162613/article/details/48323777
给定训练数据集(X,Y),其中每个样本x都包括n维特征,即x=(x1,x2,x3,...,xn)x=(x1,x2,x3,...,xn),类标记集合含有k种类别,即y=(y1,y2,...,yk),
如果现在来了一个新样本x,我们要怎么判断它的类别?从概率的角度来看,这个问题就是给定x,它属于哪个类别的概率最大。那么问题就转化为求解P(y1|x),P(y2|x),...,P(yk|x)P(y1|x),P(y2|x),...,P(yk|x)中最大的那个,即求后验概率最大的输出:argmaxykP(yk|x)



3. 三种常见的模型及编程实现
三个类适用的分类场景各不相同,一般来说,如果样本特征的分布大部分是连续值,使用GaussianNB会比较好。如果如果样本特征的分大部分是多元离散值,使用MultinomialNB比较合适。而如果样本特征是二元离散值或者很稀疏的多元离散值,应该使用BernoulliNB。
3.1 多项式模型
scikit-learn : MultinomialNB
3.2 高斯模型
scikit-learn : GaussianNB
3.3 伯努利模型
scikit-learn : BernoulliNB
补充:最大似然估计与贝叶斯估计的区别
全概率公式:对一复杂事件A的概率求解问题转化为了在不同情况下发生的简单事件的概率的求和问题
先验概率:根据以往经验和分析得到的概率
后验概率:事情已经发生,要求这件事情发生的原因是由某个因素引起的可能性的大小
最大似然估计:找到参数θ的一个估计值,使得当前样本出现的可能性最大,俗话说是“谁大像谁”。
统计学里有两个大的流派,一个是频率派,一个是贝叶斯派
最大似然估计就是频率派的典型思路
理解1:
1.最大似然估计和贝叶斯估计最大区别便在于估计的参数不同,最大似然估计要估计的参数θ被当作是固定形式的一个未知变量,然后我们结合真实数据通过最大化似然函数来求解这个固定形式的未知变量!
2.贝叶斯估计则是将参数视为是有某种已知先验分布的随机变量,意思便是这个参数他不是一个固定的未知数,而是符合一定先验分布如:随机变量θ符合正态分布等!那么在贝叶斯估计中除了类条件概率密度p(x|w)符合一定的先验分布,参数θ也符合一定的先验分布。我们通过贝叶斯规则将参数的先验分布转化成后验分布进行求解!
理解2:
简而言之,最大似然估计认为参数的所有可能取值都是一样可能的。而贝叶斯方法认为还存在一个先验估计,有些取值更有可能,有些取值更加没有可能。
理解3:
最大似然是对点估计,贝叶斯推断是对分布估计。
即,假设求解参数θ,最大似然是求出最有可能的θ值,而贝叶斯推断则是求解θ的分布。
在公式上,贝叶斯推断还引入了先验,通过先验和似然来求解后验分布,而最大似然直接使用似然函数,通过最大化其来求解




 浙公网安备 33010602011771号
浙公网安备 33010602011771号