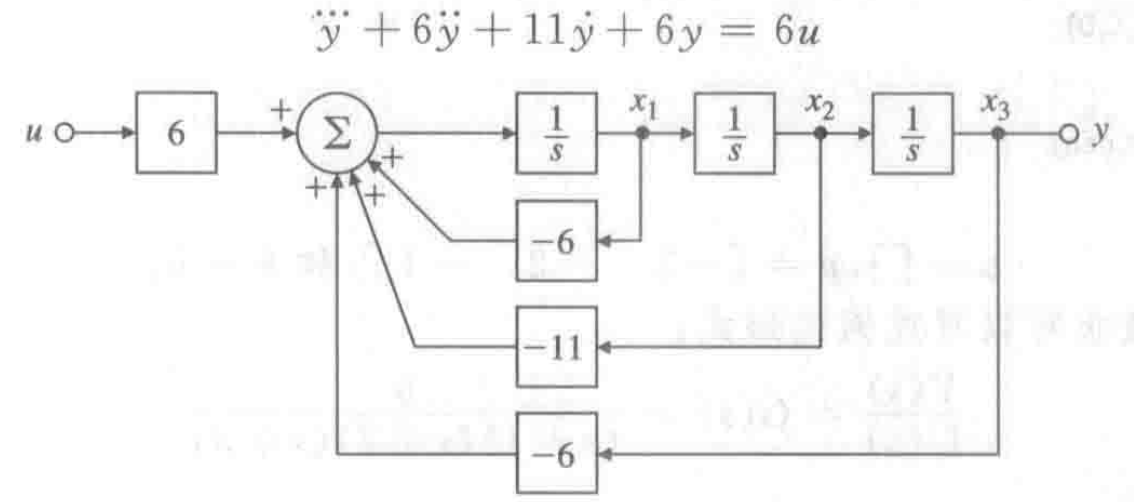
系统框图与系统的状态变量描述的微分方程和传递函数之间的关系

为了省事，直接截图：

将式子稍稍变形成：

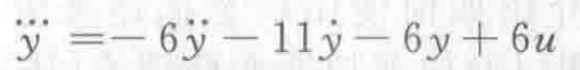
最高阶是3，需要三个微分器，加上输入和输出，根据阶的系数的不同，将对应的线连接即可，比较简单不多说明。

为了求出状态方程和传递函数，定义状态变量，x1,x2,x3,并且

dx1=-6x1-11x2-6x3+6u;  dx2=x1; dx3=x2;很容易写出状态方程，状态变量是：

 A=[-6 -11 -6; 1 0 0; 0 1 0];
 B=[6 0 0]';
 C=[0 0 1];
 D=0;

使用ss2tf将状态方程转换成传递函数的分式形式，按照幂降级系数排列，缺项用0补上。

[num,den]=ss2tf(A,B,C,D)

num =

0 0 0 6

den =

1.0000 6.0000 11.0000 6.0000

sysG=tf(num,den)

sysG =

6
----------------------
s^3 + 6 s^2 + 11 s + 6

以上的方法不容易掌握零极点信息，可以用ss2zp实现

[z,p,k]=ss2zp(A,B,C,D)

z =

空的 0x1 double 列向量

p =

-3.0000
-2.0000
-1.0000

k =

6

sysG1 =

             6
----------------------
（s+3)*(s+2)*(s+1)

其实就很容易写成因式分解的形式的，比原来的更直观些，可以选择使用。

也可以在传递函数和零极点之间转换：

[z,p,k]=tf2zp(num,den)

z =

空的 0x1 double 列向量

p =

-3.0000
-2.0000
-1.0000

k =

6

反之也是可以的。