拉普拉斯算子

　　根据向量乘法的基本原理，聪明的我们很容易知道，对于射入曲面的那一部分（左半边），其通量为负，而对于射出曲面的那一部分（右半边），其通量为正。更进一步的思考我们可以得出，相互抵消后，这一曲面上的总通量为 0

接下来我们看下一张图：

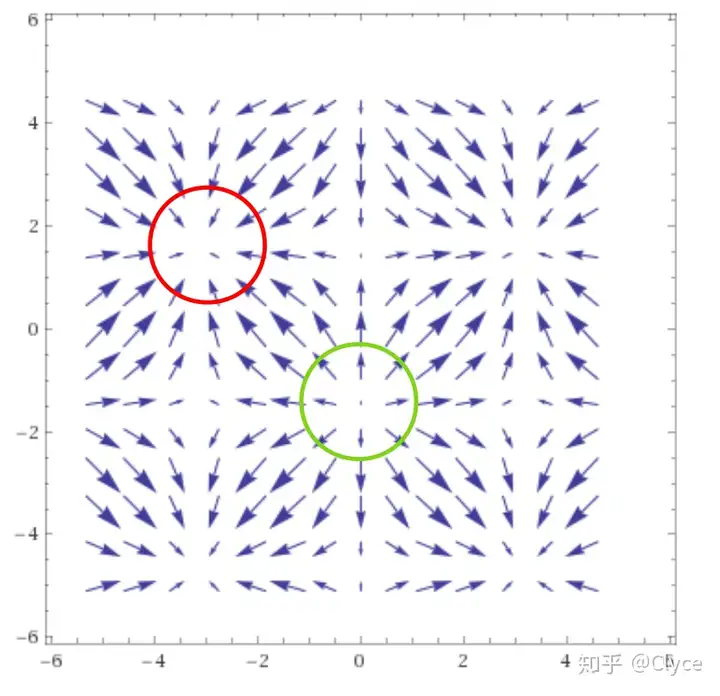
　　显然，在这一向量场中，红色曲面上的总通量为负，而绿色曲面上的总通量为正。 那么我们不断缩小这两个曲面，直至其无限接近一个点 {x} ，并将其总通量除以曲面所围成的体积 δV ，得到：

∇A=limδV→xΦA(Σ)δV ，

　　我们便得到了点 {x} 处的散度。

　　根据上面的分析，我们不难看出，在红圈所在圆心处的散度为负，而绿圈圆心处的散度为正。

结合上述定义，我们知道，散度衡量了一个点处的向量场是被发射还是被吸收，或者说，对于散度为正的点，散度越大，意味着相应的向量场越强烈地在此发散，而对于散度为负的点，意味着相应的向量场在此汇聚.。

拉普拉斯算子

接下来就是我们可爱的拉普拉斯算子啦～～

根据定义，函数 f 的拉普拉斯算子 ∇2f 又可以写成 ∇⋅∇f ，其被定义为函数 f 梯度的散度。

那么这又是什么意思呢？

我们知道，在直角坐标系下，一个函数 f(x,y,z) 在 (x0,y0,z0) 处的梯度是一个向量 (∂f∂x,∂f∂y,∂f∂z)|x=x0,y=y0,z=z0 ，

于是函数 f 的梯度函数 ∇f=∂f∂x⋅i→+∂f∂y⋅j→+∂f∂z⋅k→

就构成了一个在三维空间下的向量场。

于是乎，我们对这一向量场 ∇f 求散度 ∇⋅∇f ，即得到了 f 的拉普拉斯算子 ∇2f 。

为什么要这样做呢？

让我们想像一座山，根据梯度的定义，在山峰周围，所有的梯度向量向此汇聚，所以每个山峰处的拉普拉斯算子为负；而在山谷周围，所有梯度从此发散，所以每个山谷处的拉普拉斯算子为正。所以说，对于一个函数，拉普拉斯算子实际上衡量了在空间中的每一点处，该函数梯度是倾向于增加还是减少

歪个楼，描述物理系统最优美的公式之一拉普拉斯方程， ∇2f=0 ，大家可以想一想，这一公式表达了物理系统怎么样的特征呢？

https://zhuanlan.zhihu.com/p/67336297