概率图模型

概率图模型（ probabilistic graphical model）是一类用图来表达变量相关关系的概率模型。它以图为表示工具，最常见的是用一个结点表示一个或一组随机变量，结点之间的边表示变量间的概率相关关系，即“变量关系图”.根据边的性质不同，概率图模型可大致分为两类：第一类是使用有向无环图表示变量间的依赖关系，称为有向图模型或贝叶斯网（ Bayesian network）；第二类是使用无向图表示变量间的相关关系，称为无向图模型或马尔可夫网（ Markovnetwork）

本节将用来介绍概率图模型。

概率图模型

概率图模型（ probabilistic graphical model）是一类用图来表达变量相关关系的概率模型。它以图为表示工具，最常见的是用一个结点表示一个或一组随机变量，结点之间的边表示变量间的概率相关关系，即“变量关系图”.

分类

根据边的性质不同，概率图模型可大致分为两类：

第一类是使用有向无环图表示变量间的依赖关系，称为有向图模型或贝叶斯网（ Bayesian network）；

第二类是使用无向图表示变量间的相关关系，称为无向图模型或马尔可夫网（ Markovnetwork）；

前提背景

利用条件独立性可以降低概率模型的计算复杂度；

条件独立性要在图的结构上有所映射；

图的构建方法

拓扑排序;

根据拓扑排序构建的概率图能够得到联合概率的因子分解式；

性质：

如果父节点被观测，则其子节点独立；

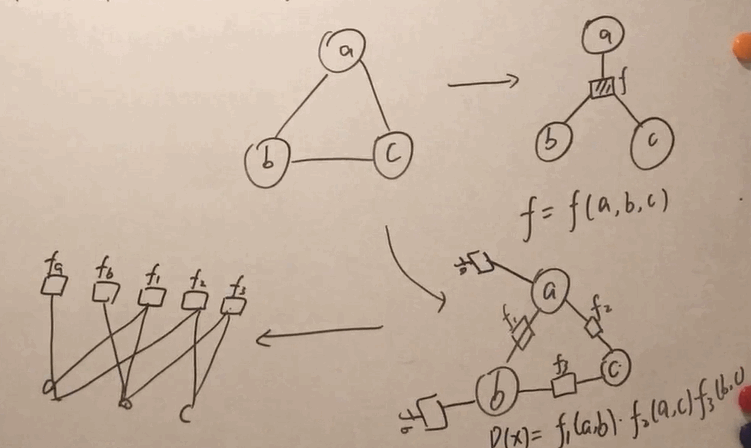
因子图

有向图：$P(x)=\Pi(x_i|x_{pa_i})$

无向图：$P(x)=\cfrac{1}{Z}\Pi^k_{i=1}\phi_{c_i}(x_{c_i})$

道德图：有向图 → 无向图

出发点：

1. 引入环
2. 简便

因子图把因子引入图里边。