视觉SLAM(五)特征点提取与匹配
特征点法视觉里程计
特征点提取与匹配
经典 SLAM 模型中以位姿 路标( Landmark )来描述 SLAM 过程
• 路标是三维空间中固定不变的点,能够在特定位姿下观测到
• 数量充足,以实现良好的定位
• 较好的区分性,以实现数据关联
在视觉 SLAM 中,可利用图像特征点作为 SLAM 中的路标
特征点是图像中具有代表性的部分;
具有可重复性,可区别性,高效,本地的特点
特征点的信息
• 位置、大小、方向、评分等 关键点
• 特征点周围的图像信息 描述子( Descriptor)
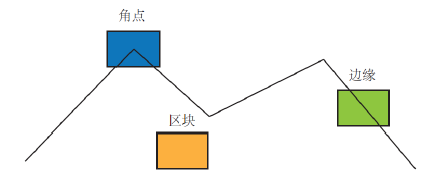
特征描述应该在光照、视角发生少量变化时仍能保持一致
例子:SIFT/SURF/ORB(见 OpenCV features2d 模块)
典型的特征点
ORB 特征
关键点: Oriented FAST
描述: BRIEF

FAST
• 连续 N 个点的灰度有明显差异
Oriented FAST
• 在 FAST 基础上计算旋转
描述子
BRIEF
• BRIEF 128 :在特征点附近的 128 次像素比较
• ORB :旋转之后的 BRIEF 描述
BRIEF 是一种二进制描述,需要用汉明距离度量
特征匹配
目的: 通过描述子的差异判断哪些特征为同一个点
暴力匹配:比较图 1 中每个特征和图 2 特征的距离
加速:快速最近邻方法(FLANN)

2D-2D 对极几何
特征匹配之后,得到了特征点之间的对应关系
• 如果只有两个单目图像,得到 2D 2D 间的关系——对极几何
• 如果匹配的是帧和地图,得到 3D 2D 间的关系——PnP
• 如果匹配的是 RGB D 图,得到 3D 3D 间的关系——ICP


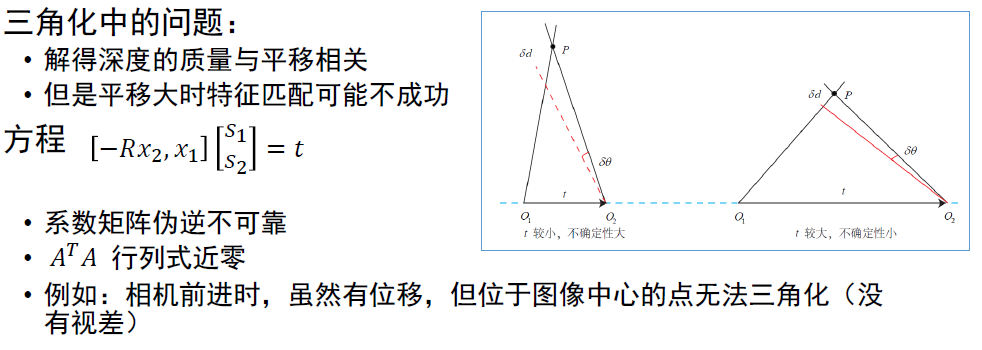
三角化与深度估计
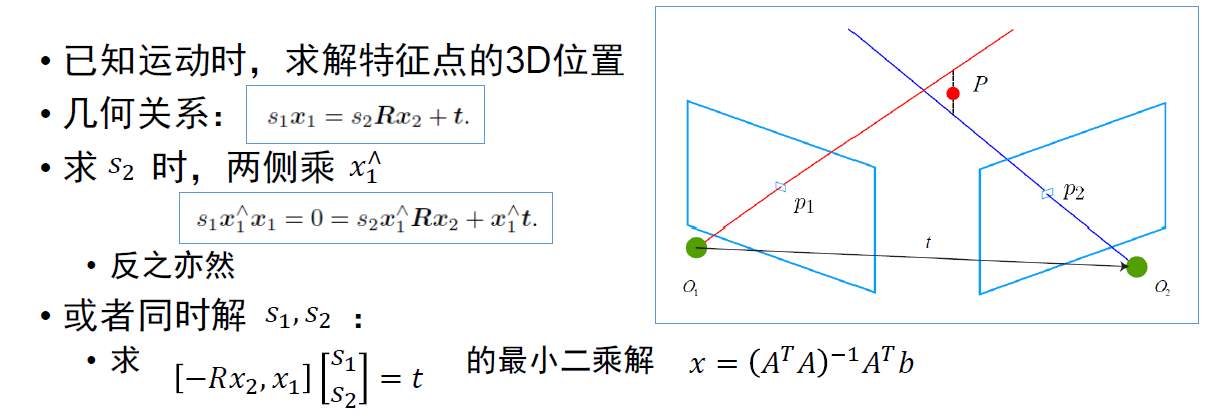
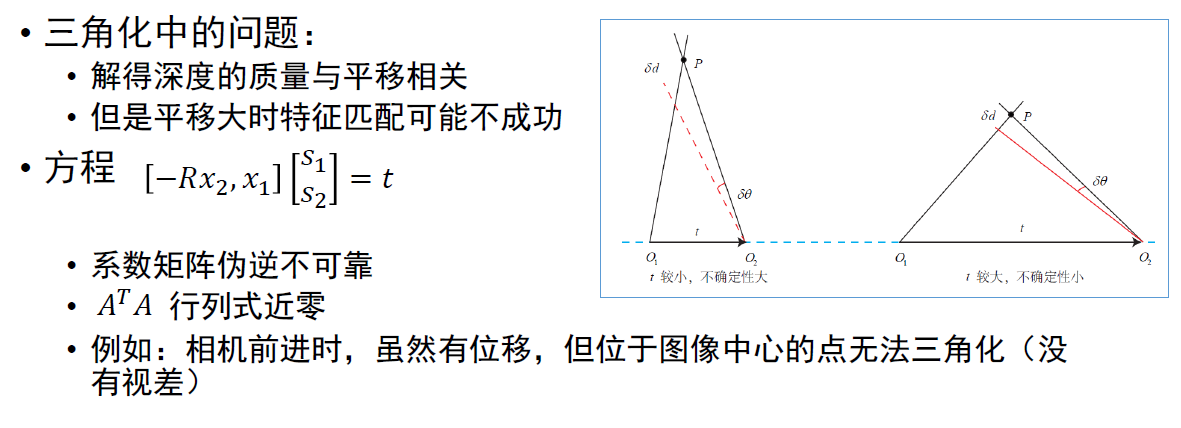
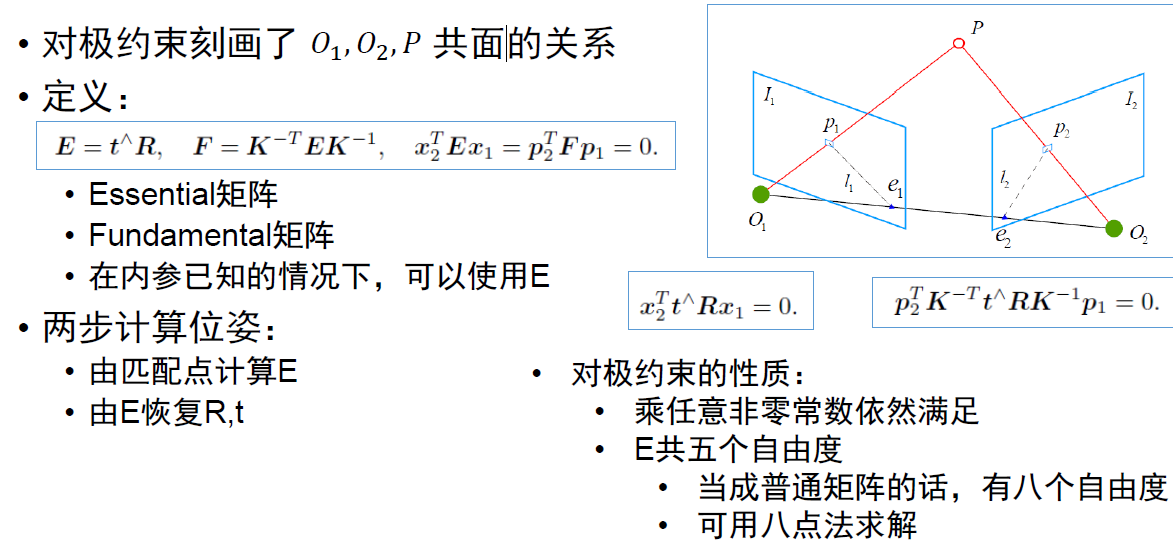
求E使用八点法来求
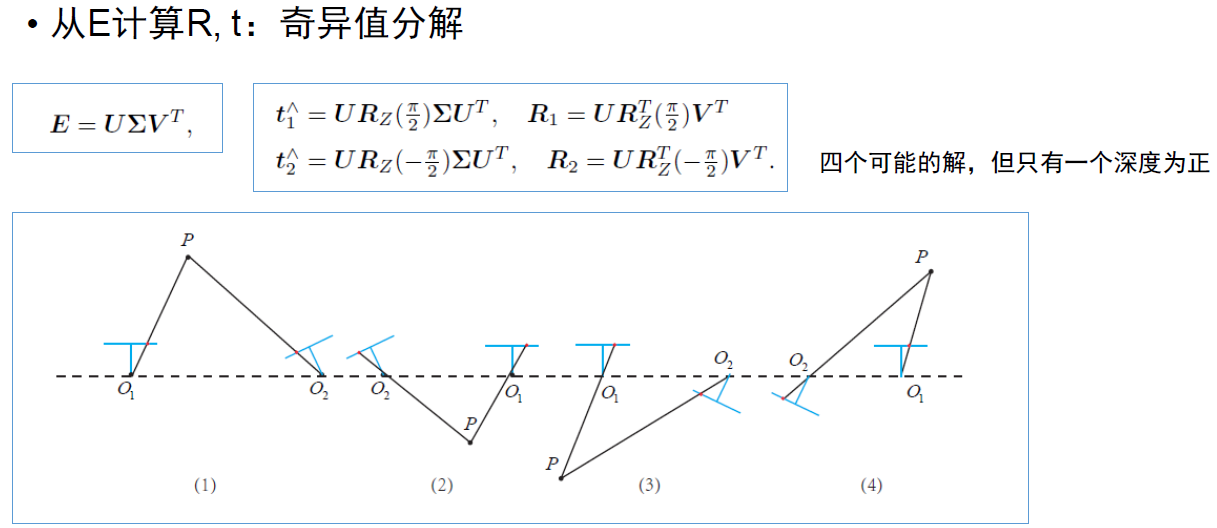

从E计算R,t则使用奇异值分解
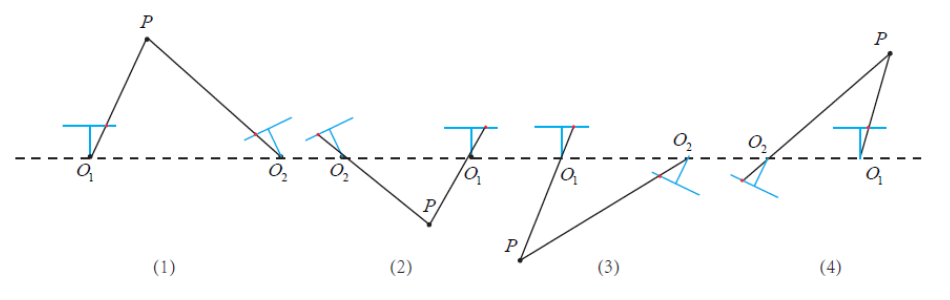
一共会生成四个可能的解,但只有一个深度为正。
SVD 过程中:取\(E = U diag (\frac{\delta_1+\delta_2}{2},\frac{\delta_1+\delta_2}{2},0)V^T\) 因为 E 的内在性质要求它的奇异值为\(\delta,\delta,0\);
• 最少可使用五个点计算 R,t ,称为五点法, 但需要利用 E 的非线性性质,原理较复杂
八点法的讨论
八点法可用于单目 SLAM 的初始化(初始化需要相机运动)
- 尺度不确定性:归一化 t 或特征点的平均深度(相机运动)
- 纯旋转问题: t=0 时无法求解
- 点对数多于八对时:则使用最小二乘法进行求解
- 有外点时:使用RANSAC进行过滤。
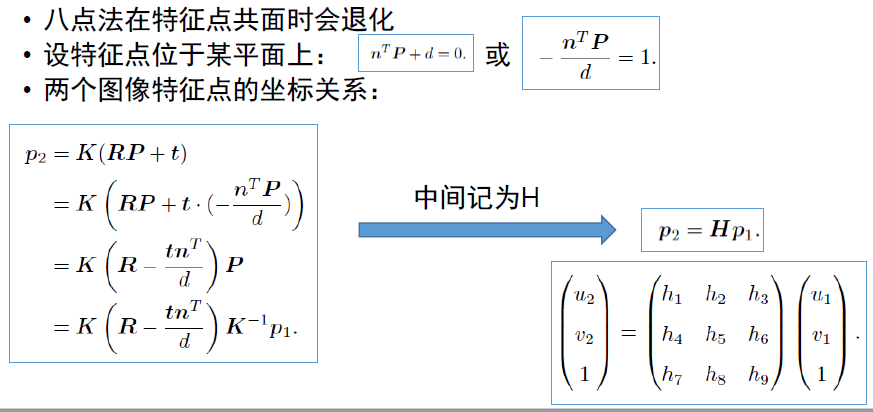
从单应矩阵恢复R,t
- 八点法在特征点共面时会共面
- 设特征点位于某平面上:\(n^TR+d=0\)或\(-\frac{n^TP}{d}=1\).
![]()
![]()
小结
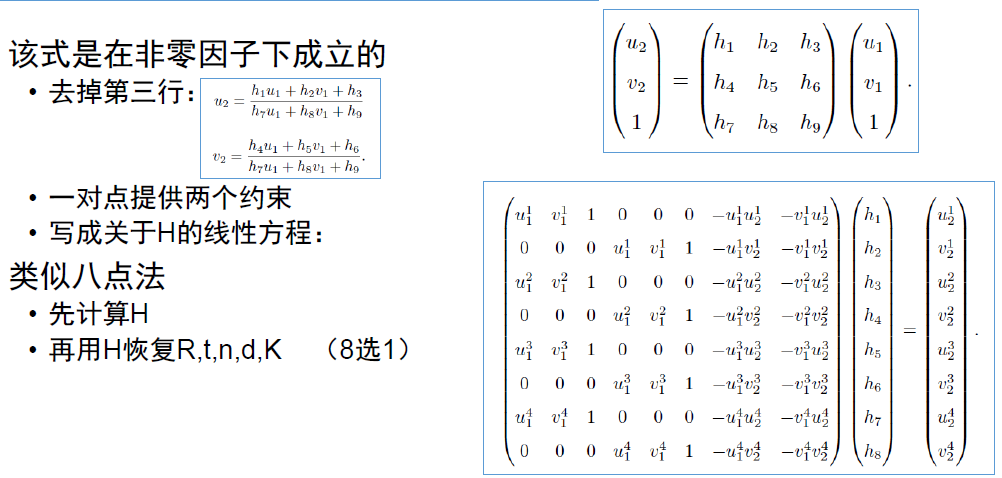
2D——2D 情况下,只知道图像坐标之间的对应关系
• 当特征点在平面上时(例如俯视或仰视),使用 H 恢复 R,t
• 否则,使用 E 或 F 恢复 R,t
• t 没有尺度
求得 R,t 后:
• 利用三角化计算特征点的 3D 位置(即深度)
• 实际中用于单目 SLAM 的初始化部分
3D-2D PnP

目的:已经 3D 点的空间位置和相机上的投影点,求相机的旋转和平移(外参)
解法:代数的解法/优化的解法
1. 代数解法
a. DLT(direct Linear Trace)
设空间点\(P=(X,Y,Z,1)^T\),投影点为:\(x=(u,v,1)\) 归一化坐标,则投影关系:\(sx=[R|t]p\)
展开:
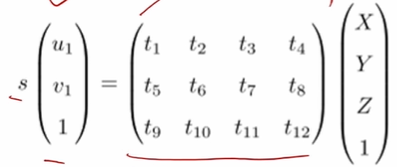
• 将它看成一个关于 t 的线性方程,求解 t
• 注意最下一行为\(s=[t_9,t_{10},t_{11},t_{12}][X,Y,Z,1]^T\)
• 用它消掉前两行中的 s ,则一个特征点提供两个方程:
为求解 12 个未知数,Y一般需要 12/2=6 对点。(超定时求最小二乘解)
• DLT 将 R,t 看成独立的未知量,所以在求出结果后,需要将 t 组成的矩阵投影回 SO(3) 3)(通常用 QR 分解实现)
• 此外,也可代入内参矩阵 K ,但 SLAM 中一般假设 K 已知,所以这里没有代入。
为求解 12 个未知数,需要 12/2=6 对点。(超定时求最小二乘解)
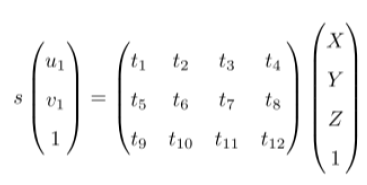
b. P3P:利用三对点求相机内参
c. EPnP /UPnP/...
2. 优化解法: Bundle Adjustment

线性化和雅可比


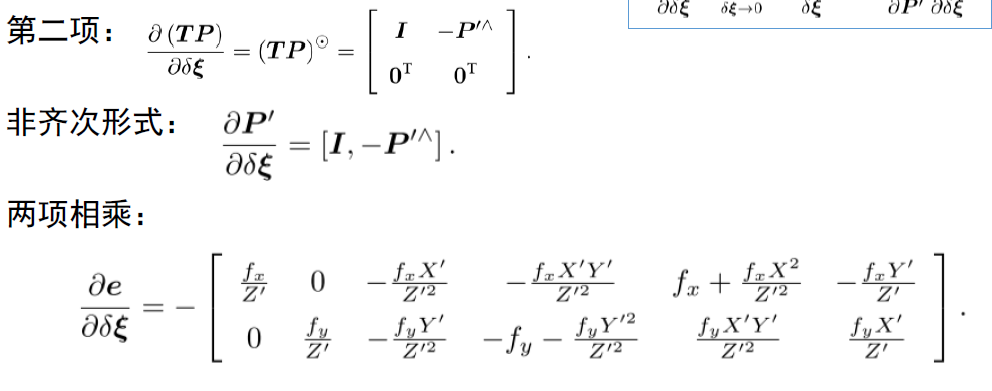
对3D点求导:

4. 3D-3D ICP

ICP 也可以从非线性优化角度求解,但:
• 已知匹配时, ICP 问题存在唯一解或无穷多解的情况。在唯一解的情况下,只要能找到极小值解,那么这个 极小值就是全局最优值 。
• 所以正常情况下, SVD 结果和优化一样,且优化很快收敛。
注:
• 在激光情况下,匹配点未知,将指定最近点为匹配点。此时问题非凸,极小值不一定为最小值。
• 利用非线性优化可以将 ICP 与 PnP 结合在一起求解。
小结
本章介绍了与特征点相关的视觉里程计部分算法,包括:
- 特征点是如何提取并匹配的;
- 如何通过2D-2D的特征点估计相机运动;
- 三角化原理;
- 3D-2D的PnP问题,线性解法与BA解法;
- 3D-3D的ICP问题,线性解法与BA解法。
5. 三角化与深度估计



 浙公网安备 33010602011771号
浙公网安备 33010602011771号