视觉SLAM（三) 李群与李代数
群
群的性质
- 旋转矩阵集合与旋转乘法构成群
- 变换矩阵与矩阵乘法构成群
- 因此可以称为旋转矩阵群和变换矩阵群
三维旋转矩阵构成了特殊正交群
其他群的例子:
- 一般线性群GL(n) n*n的可逆矩阵 它们对矩阵乘法构成群
- 特殊正交群SO(n)
- 特殊欧式群SE(n)
三维变换矩阵构成了特殊矩阵群
李群与李代数
李群:
- 具有连续(光滑)性质的群
- 既是群也是流形
- 直观上看,一个刚体能连续地在空间中运动,故SO(3)和SE(3)都是李群
- 但是,SO(3)和SE(3)只有定义良好的乘法,没有加法,所以难以进行取极限\求导等操作.
李代数:与李群对应的一种结构,位于向量空间.
- 通常记作小写的SO(3)和SE(3),书中以哥特体突出显示.
- 事实上是李群单位元处的正切空间
- 每个李群都有与之对应的李代数。李代数描述了李群单位元附近的正切空间性质
从旋转矩阵引出李代数
- 考虑任意旋转矩阵R,满足 \(RR^T=I\)
令R随时间变换(连续运动),有\(R(t){R(t)}^T=I\)
量测对时间求导:\(\hat{R(t)}{R(t)}^T+R(t){\hat{R(t)}}^T=0\)
整理:\(\hat{R(t)=\Phi(t)^{\times}R(t)}\)
两侧右乘R(t):\(\hat{R(t)=\Phi(t)^{\times}R(t)}\)
课看成对R求导之后,左侧多出一个\(\Phi(t)\)
单位元附近:\(t_0=0\),\(R(0)=I\)
已知初始情况：\(R(0)=I\),解之，得:
该式说明，对任意t，都可以找到一个R和一个\(\phi\)得对应关系
该关系指指数映射（Exponetial Map）
这里得\(\phi\)称为SO（3）对应得李代数：SO(3)
指数映射与对数映射
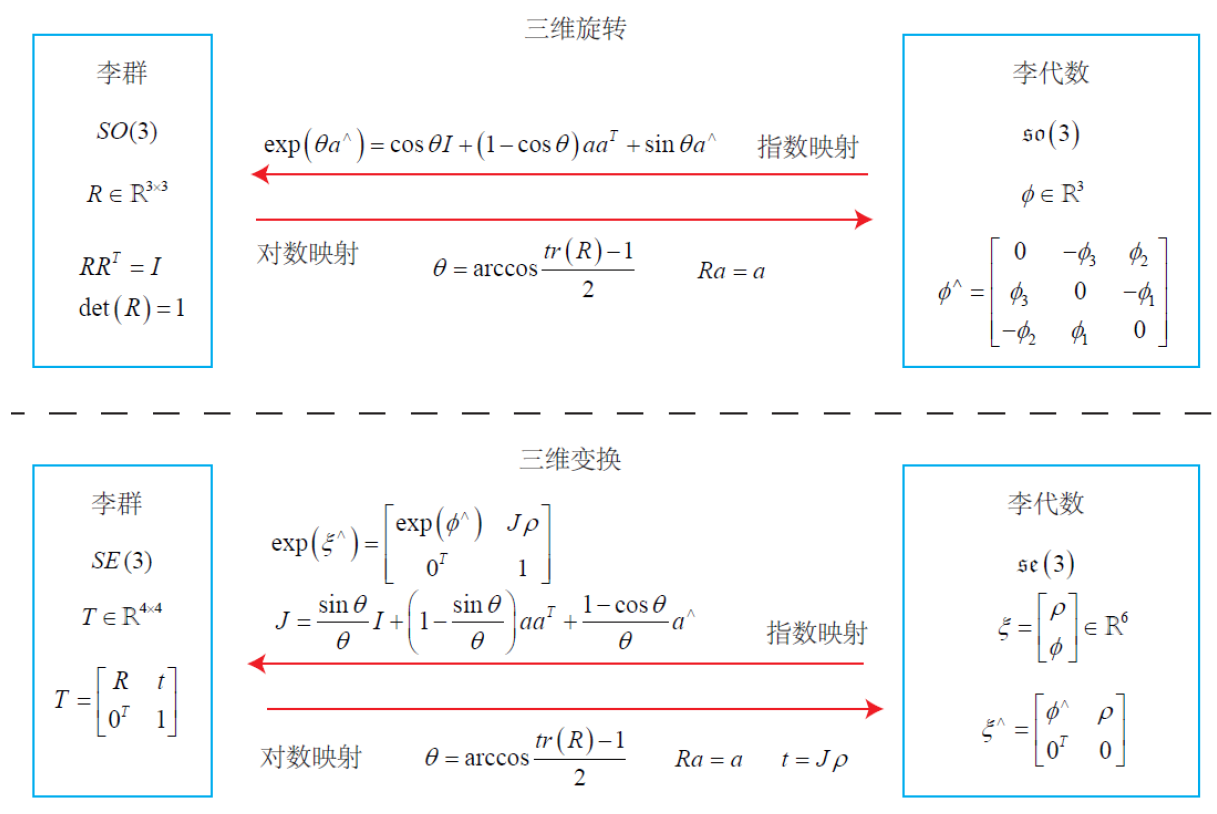
指数映射反映了从李代数到李群的对应关系：\(R=\exp(\phi^{\wedge})\)
问题：但是\(\phi^{\wedge}\)是一个矩阵，对于矩阵，如何定义求指数运算？
\(\exp(\phi^{\wedge})=\sum^{}_{n=0} \frac{1}{n!}(\phi^{\wedge})^n\)
由于\(\phi\)得向量，定义其角度和模长：
角度乘单位向量：\(\phi=\theta a\)
a的性质化解taylor展示中的高阶项提供了有效方法
Taylor展开：
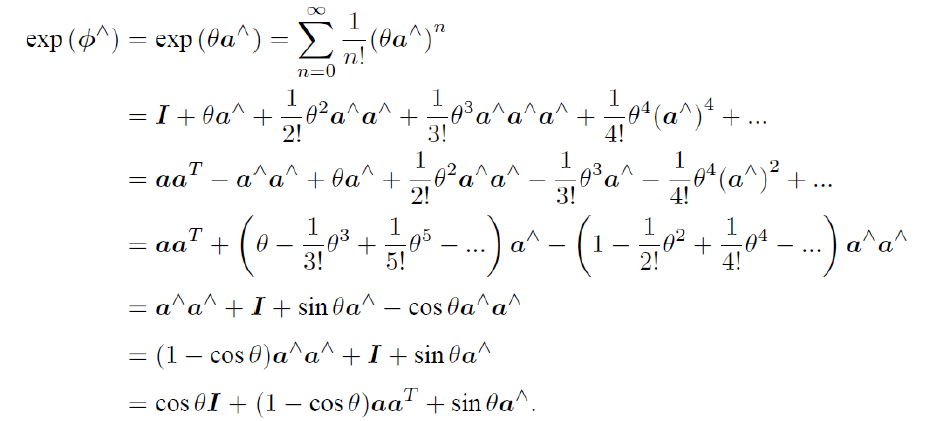
结果：\(\exp(\theta a^{\wedge}) = \cos \theta I+(1-cos\theta)aa^T+sin\theta a^{\wedge}\)
这说明SO(3)的物理意义就是旋转向量；
反之，给的旋转矩阵是，亦能求李代数：
但实际中没必要这样求，在旋转向量小姐已经介绍了矩阵到向量的转换关系：
$\theta = arccos(\frac{tr(R)-1}{2}) $ \(Rn=n\)
至此，说明了\(SO(3)\)与\(so(3)\)的对应关系。
求导与扰动模型
SLAM的定位即位姿估计
但李群无加法：\(R_1+R_2\notin SO(3)\)倒数无从定义
解决方法：
- 利用李代数上加法定义李群元素的导数？
- 使用指数映射和对数映射完成变换关系
基本问题：当在李代数中做加法时，是否等价于在李群上做乘法？
\(exp(\phi_1^{\wedge})exp(\phi_2^{\vee})=exp((\phi_1+\phi_2)^{\wedge})\)
在使用标量的情况下，该式明显成立，但这里的\(\phi^{\wedge}\)为矩阵，完整形式由BCH公式给出
BCH公式
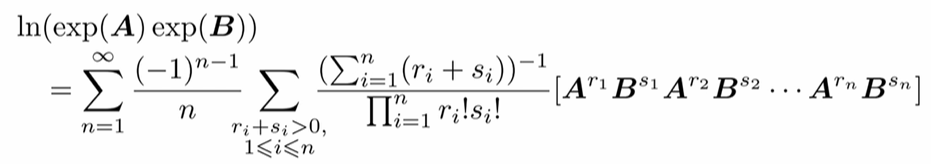
前面的几项：
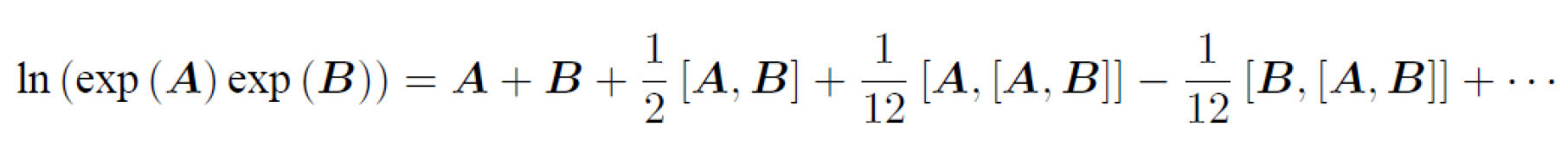
通过 BCH 线性近似，可以定义李代数上的导数
考虑一个基本问题：旋转后的点关于旋转的导数可以不严谨地记为：\(\frac{\partial (Rp)}{\partial R}\)
由于 R 没有加法，导数无从定义，此时存在两种解决办法：
• 对 R 对应的李代数加上小量，求相对于小量的变化率（导数模型）；
• 对 R 左乘或右乘一个小量，求相对于小量的李代数的变化率（扰动模型）。
导数模型
扰动模型
左乘一个小量，令其李代数为0
SE(3)上的扰动模型
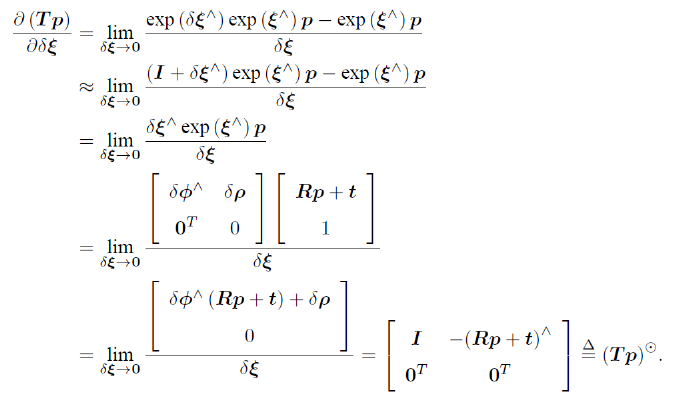
小结
• 利用 BCH 线性近似，可以推导 so(3) 与 se(3) 上的导数和扰动模型
• 通常情况下，扰动模型更为简洁实用
实践：Sophus库
#include "sophus/so3.hpp"
#include "sophus/se3.hpp"
