VINS_Fusion 初始化过程

VINS_Fusion的初始化与VINS_mono差不多.
按照<<手写VIO>>课程中的说法

1. 背景技术

在介绍VINS的初始化模块之前,先介绍以下背景知识:

A.IMU预积分

IMU传感器模型可以表示为如下式子:

\[ω̃^b = ω^b + b^g + n^g\\ ã^b = q_{bw} (a^w +g^w)+b^a+n^a \]

IMU 预积分即:将一段时间内的 IMU 数据直接积分起来就能得到两时刻 i, j 之间关于 IMU 的测量约束,即 预积分量:

\[伪位移增量：\alpha_{b_ib_j}=\int\int_{t\in[i,j]}(q_{b_ib_t}a^{b_t})\delta t^2\\ 速度预计分量：\beta_{b_ib_j}=\int_{t\in[i,j]}(q_{b_ib_t}a^{b_t})\delta t\\ 两帧之间的旋转：q_{b_ib_t}=\int_{t\in[t,j]}q_{b_ib_t} \left[\begin{matrix}0\\1/2w^{b_t}\end{matrix}\right]dt \]

上式中,位移增量为什么是伪位移增量呢,因为加速度为0的时候,相机的速度不一定为0;
根据上述的数学模型,我们可以计算两个时刻之间IMU的轨迹.

B.视觉几何基础

根据得到的两张图片,可以通过如下过程来计算相机的变换.

1. 已知两图像：特征点提取，匹配（光流，特征描述子）
2. 已知俩图像特征匹配点:利用对极几何约束 (E 矩阵,H 矩阵), 计算两图像之间的 pose (update to scale).
3. 已知相机 pose, 已知特征点二维坐标: 通过三角化得到三维坐标.
4. 已知 3d 点,2d 特征点:通过 Perspective-n-Point(PnP) 求取新的 相机 pose

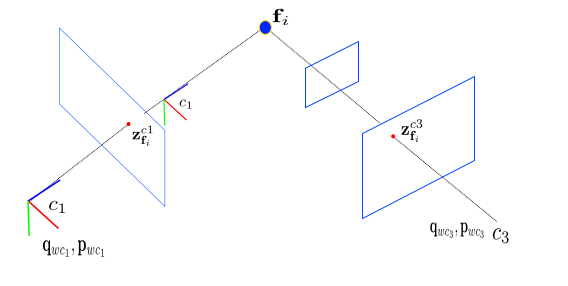
根据上述过程,我们可以根据相机的图片信息得到图片之间的变换.

两套轨迹带来的问题->如何融合？

根据前两个模型,我们得到了两套的轨迹.对于这两套轨迹,我门有以下问题:

1. IMU 怎么和世界坐标系对齐,计算初始时刻的 \(q_{wb_0}\) ?
2. 单目视觉姿态如何和 IMU 轨迹对齐,尺度如何获取?
3. VIO 系统的初始速度 v,传感器 bias 等如何估计?
4. IMU 和相机之间的外参数等...

VINS的初始化

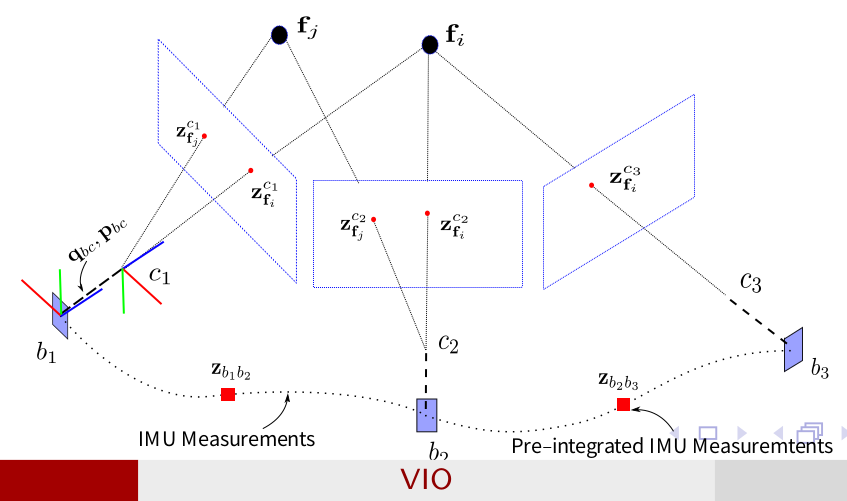
1.视觉与IMU之间的联系

基于这些联系构建几何约束

考虑相机坐标系 \(c_0\) 为世界坐标系,则利用外参数 \(q_{bc} , t_{bc}\) 构建等式

\[q_{c_0b_k} = q_{c_0b_k}⊗ q^{-1}_{bc}\\ s\overline{p}_{c_0b_k} = s\overline{p}_{c_0c_k}−R_{c_0b_k}p_ {bc} \]

带一横表示带了尺度。其中,s 为尺度因子,\(\overline{p}\) 表示非米制单位的轨迹。等式(3)等价于

\[\overline{p}_{c_0b_k} = \overline{p}_{c_0c_k}−\frac{1}{s}R_{c_0b_k}p_ {bc}\\ \overline{p}_{c_0c_k} = \frac{1}{s}R_{c_0b_k}p_ {bc}+\overline{p}_{c_0b_k} \]

旋转没有尺度信息。

通过该约束来与相机提供的约束打通关系。

2.视觉IMU对齐流程

估计流程

1. 旋转外参数 \(q_{bc}\) 未知, 则先估计旋转外参数.（很多时候由于相机与IMU很近，因此平移参数不是很重要）

2. 利用旋转约束估计陀螺仪 bias.（短时间内是个常数，因此需要估计以得到更准确的值）

   \[q_{c_0b_k} = q_{c_0c_k} ⊗ q^{-1}_{bc} \]

3. 利用平移约束估计重力方向,速度,以及尺度初始值.(把非米制单位拉伸到米制单位)

   \[s\overline{p}_{c_0b_k} = s\overline{p}_{c_0c_k} − R_{c_0b_k}p_{bc} \]

4. 对重力向量 \(g^{c_0}\) 进行进一步优化.

5. 求解世界坐标系 w 和初始相机坐标系 \(c_0\) 之间的旋转矩阵 \(q_{wc_0}\),
   并将轨迹对齐到世界坐标系。

A. 利用旋转约束估计外参数旋转\(Q_{bc}\)

相邻两时刻 k, k + 1 之间有:IMU旋转积分 \(q_{b_kb_{k+1}}\) ,视觉测量\(q_{c_kc_{k+1}}\) 。则有:

\[q_{b_kb_{k+1}}⊗q_{bc} = q_{bc}⊗q_{c_kc_{k+1}}=0 \]

上式可写成:

\[([q_{b_kb_{k+1}}]_L-[q_{c_kc_{k+1}}]_R)q_{bc}= Q^{k}_{k+1}q_{bc}=0 \]

其中,\([·]_L , [·]_R\) 表示 left and right quaternion multiplication。

将多个时刻线性方程(6)累计起来(提高信噪比),并加上鲁棒核权重得到:

\[\left[\begin{matrix} w^0_1Q^0_1\\w^1_2Q^1_2\\...\\w^{N-1}_NQ^{N-1}_N \end{matrix}\right] q_{bc}=Q_Nq_{bc}=0 \]

其中

\[w^k_{k+1}=\left\{\begin{array}{l} 1,& r^{k}_{k+1}<thresold\\ \frac{thresold}{r^{k}_{k+1}},& otherwise \end{array}\right. \]

由旋转矩阵和轴角之间的关系 \(tr(R) = 1 + 2 cos θ\), 能得到角度误差 r
的计算为:

\[r^k_{k+1}=acos((tr(\hat{R}^{-1}_{bc}{R}^{-1}_{b_kb_{k+1}}\hat{R}_{bc}{R}_{b_kb_{k+1}})-1)/2) \]

即从视觉数据计算得到的R应当与Q相同，因此括号中应该为一个单位矩阵

公式(7)的求解同样采用 SVD 分解,即最小奇异值对应的奇异向量。

具体代码见：initial_ex_rotation.cpp 函数 CalibrationExRotation()。

B. 基于旋转约束的Gyroscope Bias

• 估计bias可以使两个时刻之间IMU的旋转更准。因为旋转是通过积分得到的。

• 假定\(q_{c_kc_{k+1}}\)准确，且g估计到的外参准确，则\(q_{c_kb_k}\)准确.

如果外参数 \(q_{bc}\) 已标定好,利用旋转约束,可估计陀螺仪 bias:

\[arg \min_{\delta b^g}\sum_{k\in\Beta}||2|q^{-1}_{c_0b_{k+1}}⊗q_{c_0b_k}⊗q_{b_kb_{k+1}}|_{xyz}||^2 \]

其中, B 表示所有的图像关键帧集合,另有预积分的一阶泰勒近似:

\[q_{b_kb_{k+1}}\approx \hat{q}_{b_kb_{k+1}}⊗ \left[\begin{array}{c} 1\\\frac{1}{2}J^q_{b^g}\delta b^g \end{array}\right] \]

\(q_{b_kb_{k+1}}\)的误差近似于第二项。

公式(10)为普通的最小二乘问题,求取雅克比矩阵,构建正定方程 HX = b =0 即可以求解 。

具体代码见:initial_aligment.cpp 函数 solveGyroscopeBias().

C. 初始化速度、重力和尺度因子

研究将IMU与相机对齐之后如何初始化速度、重力和尺度因子。

待估计变量

\[\chi_I=[v^{b_0}_0,v^{b_1}_1,...,v^{b_n}_n,g^{c_0},s]^T \]

其中,\(v_k^{b_k}\)表示k时刻body 坐标系的速度在 body 坐标系下的表示。
\(g^{c_0}\)为重力向量在第 0 帧相机坐标系下的表示。s 表示尺度因子,将视
觉轨迹拉伸到米制单位。

回顾：预积分量约束

世界坐标系w下有

\[\alpha_{b_ib_j}=q_{b_iw}(p_{wb_j}-p_{wb_i}-v^w_i\Delta t+\frac{1}{2}g^w\Delta t^2)\\ \beta_{b_ib_j}=q_{b_iw}(v^w_j-v^w_i+g^w\Delta t) \]

将世界坐标系 w 换成相机初始时刻坐标系 \(c_0\) 有

\[\alpha_{b_kb_{k+1}}=R_{b_kc_0}(s(\overline{p}_{c_0b_{k+1}}-\overline{p}_{c_0b_k}))+\frac{1}{2}g^{c_0}\Delta t^2_k -R_{c_0b_k}v^{b_k}_k\Delta{t_k}\\ \beta{b_kb_{k+1}}=R_{b_kc_0}(R_{c_0b_{k+1}}v_{k+1}^{b_{k+1}}+g^{c_0}\Delta t^2_k -R_{c_0b_k}v^{b_k}_k\Delta{t_k} \]

将公式(3)代入公式(14)进行简单整理有:

\[\alpha_{b_kb_{k+1}}=sR_{b_kc_0}(\overline{p}_{c_0c_{k+1}}-\overline{p}_{c_0c_k})-R_{b_kc_0}R_{c_0b_{k+1}}p_{bc}+p_{bc}+\frac{1}{2}R_{b_kc_0}g^{c_0}\Delta t^2_k-v_k^{b_k}\Delta t_k \]

将待估计变量放到方程右边，有：

具体代码见:initial_aligment.cpp 函数 LinearAlignment().

D. 优化重力向量\(g^{c_0}\)

疑问:为什么需要优化重力向量

利用公式(16)求解重力向量 g_{c_0} 过程中,并没有加入模长限制
\(∥g^{c_0}∥ = 9.81\)。三维变量 \(g^{c_0}\) 实际只有两个自由度。

重力向量的参数化

三维向量自由度为 2,可以采用球面坐标
进行参数化:

\[ĝ^{c_0} = ∥g∥·ĝ^{c_0}+w_1b_1 + w2b_2 \]

其中,w1, w2 为待优化变量

\[b_1=\left\{\begin{array}{l} \hat{\overline{g}}^{c_0}\times [1,0,0],& \hat{\overline{g}}^{c_0} \neq [1,0,0]^T\\ \hat{\overline{g}}^{c_0}\times [0,0,1],& otherwise \end{array}\right.\\ b_2 = \hat{\overline{g}}^{c_0}\times b_1 \]

将公式g代入，待优化变量变为：

\[\chi_I= \left[ \begin{matrix} v^{b_k}_k\\v^{b_{k+1}}_{k+1}\\g^{c_0}\\s \end{matrix}\right] \rarr \left[ \begin{matrix} v^{b_k}_k\\v^{b_{k+1}}_{k+1}\\w^{c_0}\\s \end{matrix}\right] \]

公式中的观测方程变为：

\[\hat{z}^{b_k}_{b_k+1} = \left[\begin{matrix} \alpha_{b_kb_{k+1}}-p_{bc}+R_{b_kc_0}R_{c_0b_{k+1}}p_{bc}-\frac{1}{2}R_{b_kc_0}\Delta t^2_k||g||\hat{\overline{g}}^{c_0} \\ \beta_{b_kb_{k+1}}-R_{b_kc_0}\Delta t_k ||g|| \hat{\overline{g}}^{c_0} \end{matrix}\right] \]

然后采用最小二乘对\(\chi_I\)重新进行优化。

E. 将相机坐标系对齐到世界坐标系

对齐流程

1. 找到 \(c_0\) 到 w 系的旋转矩阵 \(R_{wc_0} = \exp([θu])\)

   \[$u =\frac{ĝ^{c_0}\times ĝ^w}{∥ĝ^{c_0}×ĝ^w∥} θ = atan2(∥ĝ^{c_0}\times ĝ^w ∥,ĝ^{c_0}·ĝ^w) \]

2. 把所有 \(c_0\) 坐标系下的变量旋转到 \(w\) 下。

3. 把相机平移和特征点尺度恢复到米制单位。

4. 至此,完成了系统初始化过程

初始化拓展

疑问

1. 加速度 bias 为何没有估计? 加速度bias一般很小，不一定能估计出来，与重力向量相比，量纲很小

2. 平移外参数 \(p_{bc}\) 为何没有初始化?

   答：影响不大。1.陀螺仪的bias会影响旋转，旋转是一个非线性的东西，平移是线性的东西。旋转比平移重要。2. 平移外参一般在设备上很小，影响不大，可提前设置一个值，在后续中优化。

其他初始化方法

1. 静止初始化:直接用加速度测量重力方向,初始速度为 0.
2. 除 vins-mono 外的其他运动初始化方案 a , b 。

• Janne Mustaniemi et al. “Inertial-based scale estimation for structure from motion on mobile devices”. In: 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE. 2017, pp. 4394–4401.
• Javier Domínguez-Conti et al. “Visual-Inertial SLAM Initialization: A General Linear Formulation and a Gravity-Observing Non-Linear Optimization”. In: 2018 IEEE International Symposium on Mixed and Augmented Reality (ISMAR). IEEE. 2018, pp. 37–45.