博客作业06--图
1.学习总结
1.1图的思维导图
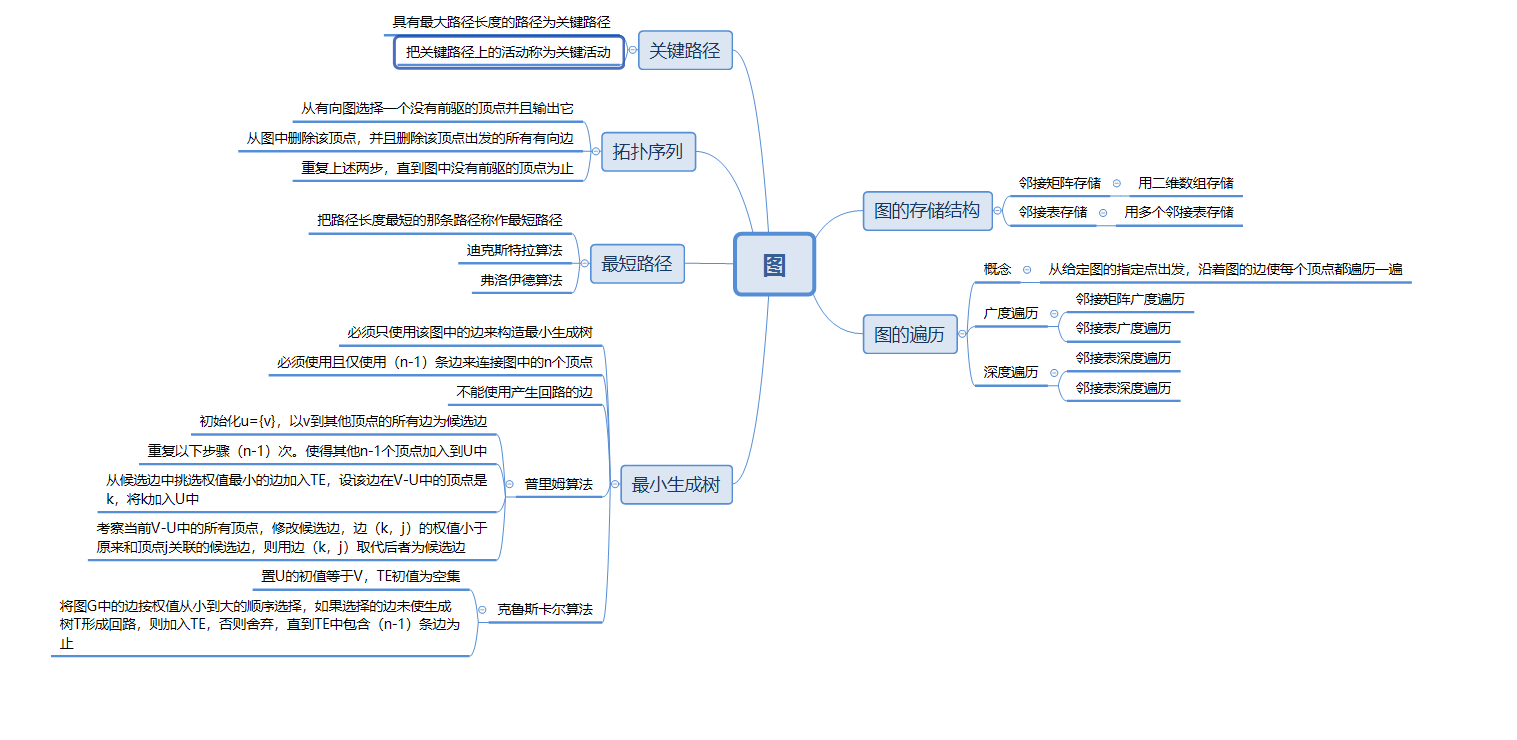
1.2 图结构学习体会
- 1、深度优先算法占内存少但速度较慢，广度优先算法占内存多但速度较快，在距离和深度成正比的情况下能较快地求出最优解。
2、深度优先与广度优先的控制结构和产生系统很相似，唯一的区别在于对扩展节点选取上。由于其保留了所有的前继节点，所以在产生后继节点时可以去掉一部分重复的节点，从而提高了搜索效率。
3、这两种算法每次都扩展一个节点的所有子节点，而不同的是，深度优先下一次扩展的是本次扩展出来的子节点中的一个，而广度优先扩展的则是本次扩展的节点的兄弟点。在具体实现上为了提高效率,
所以采用了不同的数据结构。 - 1.普里姆（Prim)算法
特点：时间复杂度为O(n2).适合于求边稠密的最小生成树.
2.克鲁斯卡尔（Kruskal)算法
特点：时间复杂度为O(eloge)(e为网中边数）,适合于求稀疏的网的最小生成树 - 优先队列实现的dijkstra速度较快，但dijkstra不能处理负权边
- 初始化栈S，计数变量cnt;
扫描顶点表，将入度为0的顶点压栈
当栈非空时循环：
栈顶结点ViVi出栈，输出VjVj，并且cnt++;
将顶点VjVj的各个邻接点入度减1；
将新的入度为0的顶点入栈
2.PTA实验作业
2.1 题目1：7-1 图着色问题
2.2 设计思路
* 遍历邻接表头
* 遍历邻接表头的结点与表头颜色比较
如果颜色相同，则return错误
* return正确
2.3 代码截图
2.4 PTA提交列表说明
- 没有考虑图不连通的时候，导致部分正确，没有考虑到color数目的的判断，也导致部分正确，后来都考虑到了，
得到了正确答案
2.1 题目1：7-2 排座位
2.2 设计思路
* 如果两位宾客之间是朋友，且没有敌对关系，则输出No problem；
* 如果他们之间并不是朋友，但也不敌对，则输出OK；
* 如果他们之间有敌对，然而也有共同的朋友，则输出OK but...；
* 如果他们之间只有敌对关系，则输出No way。
2.3 代码截图
2.4 PTA提交列表说明
- 这道题其实根据题意就很容易得出答案，其中最大N我也是百度才解决掉
2.1 题目1：7-3 六度空间
2.2 设计思路
int BFS(AdjGraph *G,int v) //v节点开始广度遍历
{
定义整形变量 count,l=0,flag1,flag2; //
定义 * p;
queue<int> Q;
visited[v]=1;
count=1;
Q.push(v);flag1=v;
while(!Q.empty()){
int temp等于Q.front(),i,j;
销毁Q;
p等于G->adjlist[temp].firstarc;
while(p不为空){
如果(visited[p->adjvex]没有进入队列){
visited[p->adjvex]标记进入队列
Q.push(p->adjvex)入队列
count++;
flag2=p->adjvex;
}
p=p->nextarc;
}
如果(temp等于flag1){
l++;
flag1=flag2;
}
如果(l等于6)
return count;
}
2.3 代码截图
2.4 PTA提交列表说明，
- 这题就是在广度优先遍历上进行改动，其中出现部分正确的原因在于对count值，i值在计算中出现了一些错误
改动一些就好了。
3.截图本周题目集的PTA最后排名
3.1 PTA排名
3.2 我的总分：2.5分
4. 阅读代码
#include <stdio.h>
#include <malloc.h>
#define MaxSize 100
#define M 4
#define N 4
//以下定义邻接表类型
typedef struct ANode //边的结点结构类型
{
int i,j; //该边的终点位置(i,j)
struct ANode *nextarc; //指向下一条边的指针
} ArcNode;
typedef struct Vnode //邻接表头结点的类型
{
ArcNode *firstarc; //指向第一条边
} VNode;
typedef struct
{
VNode adjlist[M+2][N+2]; //邻接表头节点数组
} ALGraph; //图的邻接表类型
typedef struct
{
int i; //当前方块的行号
int j; //当前方块的列号
} Box;
typedef struct
{
Box data[MaxSize];
int length; //路径长度
} PathType; //定义路径类型
int visited[M+2][N+2]= {0};
int count=0;
void CreateList(ALGraph *&G,int mg[][N+2])
//建立迷宫数组对应的邻接表G
{
int i,j,i1,j1,di;
ArcNode *p;
G=(ALGraph *)malloc(sizeof(ALGraph));
for (i=0; i<M+2; i++) //给邻接表中所有头节点的指针域置初值
for (j=0; j<N+2; j++)
G->adjlist[i][j].firstarc=NULL;
for (i=1; i<=M; i++) //检查mg中每个元素
for (j=1; j<=N; j++)
if (mg[i][j]==0)
{
di=0;
while (di<4)
{
switch(di)
{
case 0:
i1=i-1;
j1=j;
break;
case 1:
i1=i;
j1=j+1;
break;
case 2:
i1=i+1;
j1=j;
break;
case 3:
i1=i, j1=j-1;
break;
}
if (mg[i1][j1]==0) //(i1,j1)为可走方块
{
p=(ArcNode *)malloc(sizeof(ArcNode)); //创建一个节点*p
p->i=i1;
p->j=j1;
p->nextarc=G->adjlist[i][j].firstarc; //将*p节点链到链表后
G->adjlist[i][j].firstarc=p;
}
di++;
}
}
}
//输出邻接表G
void DispAdj(ALGraph *G)
{
int i,j;
ArcNode *p;
for (i=0; i<M+2; i++)
for (j=0; j<N+2; j++)
{
printf(" [%d,%d]: ",i,j);
p=G->adjlist[i][j].firstarc;
while (p!=NULL)
{
printf("(%d,%d) ",p->i,p->j);
p=p->nextarc;
}
printf("\n");
}
}
void FindPath(ALGraph *G,int xi,int yi,int xe,int ye,PathType path)
{
ArcNode *p;
visited[xi][yi]=1; //置已访问标记
path.data[path.length].i=xi;
path.data[path.length].j=yi;
path.length++;
if (xi==xe && yi==ye)
{
printf(" 迷宫路径%d: ",++count);
for (int k=0; k<path.length; k++)
printf("(%d,%d) ",path.data[k].i,path.data[k].j);
printf("\n");
}
p=G->adjlist[xi][yi].firstarc; //p指向顶点v的第一条边顶点
while (p!=NULL)
{
if (visited[p->i][p->j]==0) //若(p->i,p->j)方块未访问,递归访问它
FindPath(G,p->i,p->j,xe,ye,path);
p=p->nextarc; //p指向顶点v的下一条边顶点
}
visited[xi][yi]=0;
}
int main()
{
ALGraph *G;
int mg[M+2][N+2]= //迷宫数组
{
{1,1,1,1,1,1},
{1,0,0,0,1,1},
{1,0,1,0,0,1},
{1,0,0,0,1,1},
{1,1,0,0,0,1},
{1,1,1,1,1,1}
};
CreateList(G,mg);
printf("迷宫对应的邻接表:\n");
DispAdj(G); //输出邻接表
PathType path;
path.length=0;
printf("所有的迷宫路径:\n");
FindPath(G,1,1,M,N,path);
return 0;
}
*（1）建立迷宫对应的图数据结构，并建立其邻接表表示。（2）采用深度优先遍历的思路设计算法，输出从入口(1,1)点到出口(M,N)的所有迷宫路径。
主要是通过试探，试探可走的路，走过路进行标记，并且标记其父亲节点，如果不能走，就通过其父亲节点回归，在继续试探，同理广度历也同样
适用。
