博客作业01-抽象数据类型
一.作业题目
仿照三元组或复数的抽象数据类型写出有理数抽象数据类型的描述 (有理数是其分子、分母均为整数且分母不为零的分数)。
有理数基本运算:
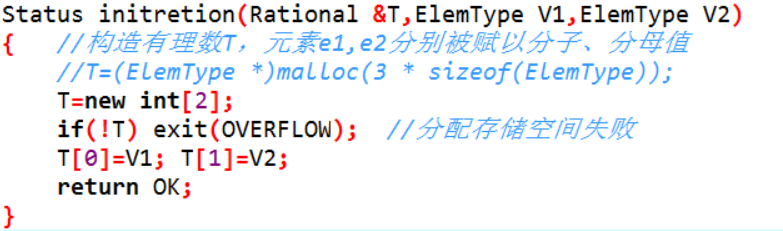
1.构造有理数T,元素e1,e2分别被赋以分子、分母值
2.销毁有理数T
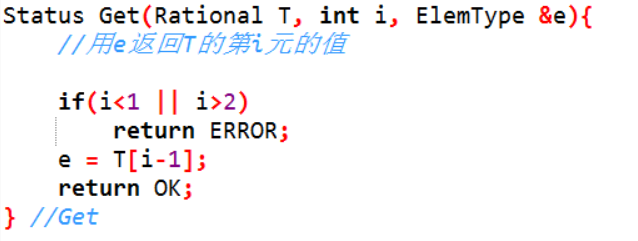
3.用e(引用类型参数)返回有理数T的分子或分母,当入参i为1时返回分子, i为2是返回分母。
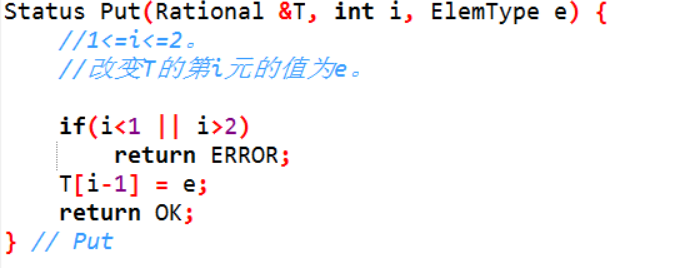
4.将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母
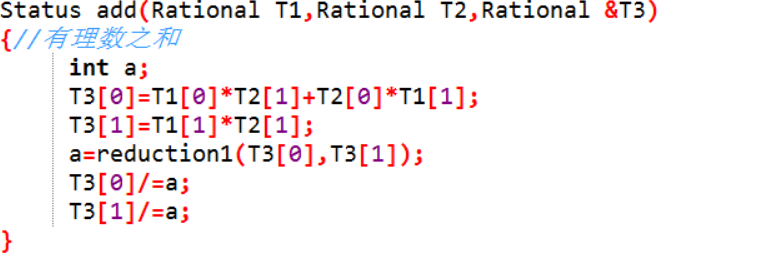
5.有理数T1,T2相加,结果存入有理数T3
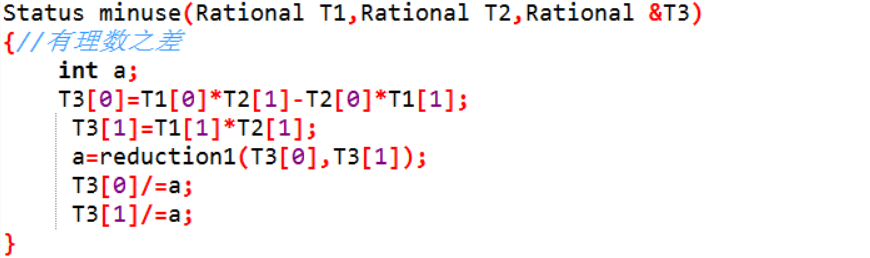
6.有理数T1,T2相减,结果存入有理数T3
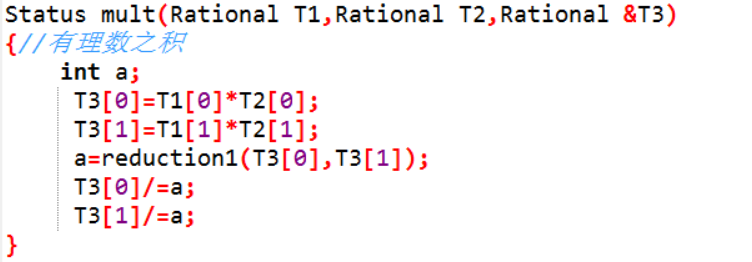
7.有理数T1,T2相乘,结果存入有理数T3
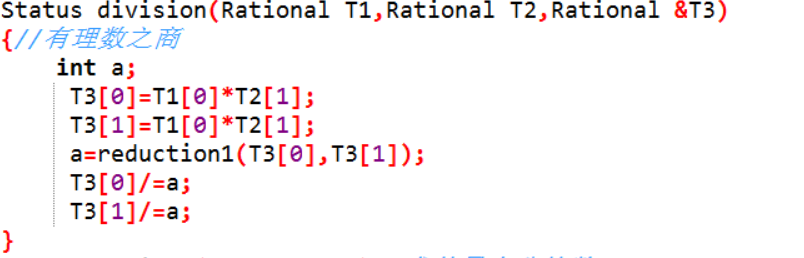
8.有理数T1,T2相除,结果存入有理数T3
二、实验
1.用ADT的抽象数据模型描述你的有理数数据类型。
ADT Rational{
数据对象: D={e1,e2|都是ElemType类型}
数据关系: R={<e1,e2>}
基本操作:
Rational initretion(Rational *T0);//构造有理数T,元素e1,e2分别被赋以分子、分母值
ElemType Get(Rational *T0,int i);//用e(引用类型参数)返回有理数T的分子或分母,当入参i为1时返回分子, i为2是返回分母。
ElemType Put(Rational *T0,int i,ElemType e);//将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母
void add(int a1,int b1,int a2,int b2);//有理数之和
void minuse(int a1,int b1,int a2,int b2);//有理数之差
void mult(int a1,int b1,int a2,int b2);//有理数之积
void division(int a1,int b1,int a2,int b2);//有理数之商
int reduction1(int a,int b);//求公约数
}ADT Rational
2.数据结构、函数说明


3.代码实现说明
-
有理数之和
-
有理数之差
-
有理数之积
-
有理数之商
-
构造有理数
-
销毁有理数

-
返回有理数的分子或分母函数
-
改变有理数分子或分母元素
三.代码互评
-
我的代码

-
杰伟的代码
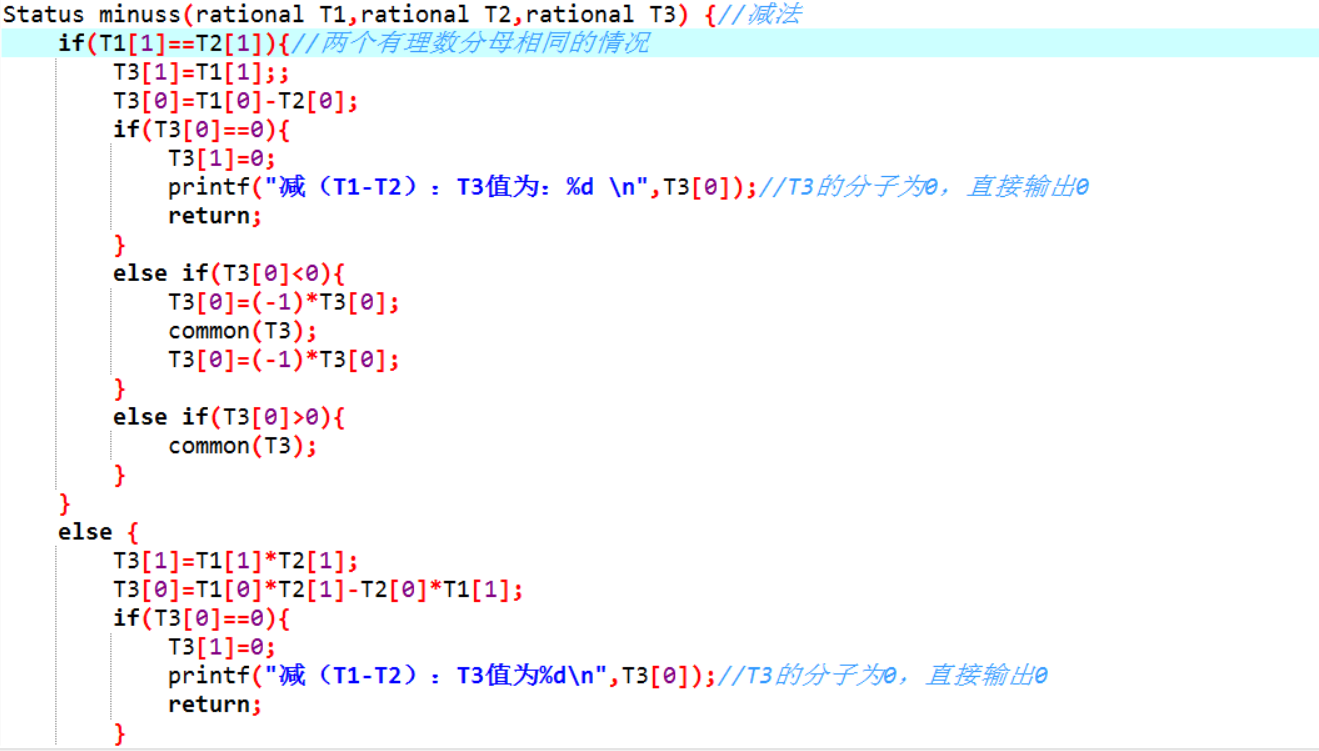
- 从有理数之商,杰伟的代码考虑的很充分,考虑到分母为0,分子为0的情况, 我的就欠缺考虑了。
四.结果展示
-
正确输入
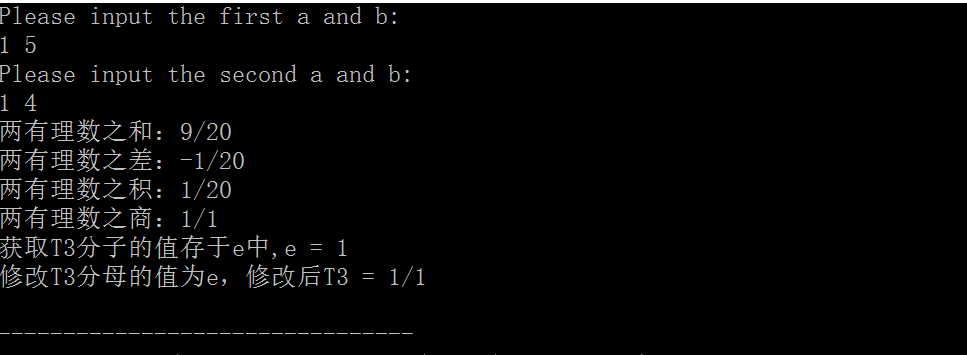
-
非法输入
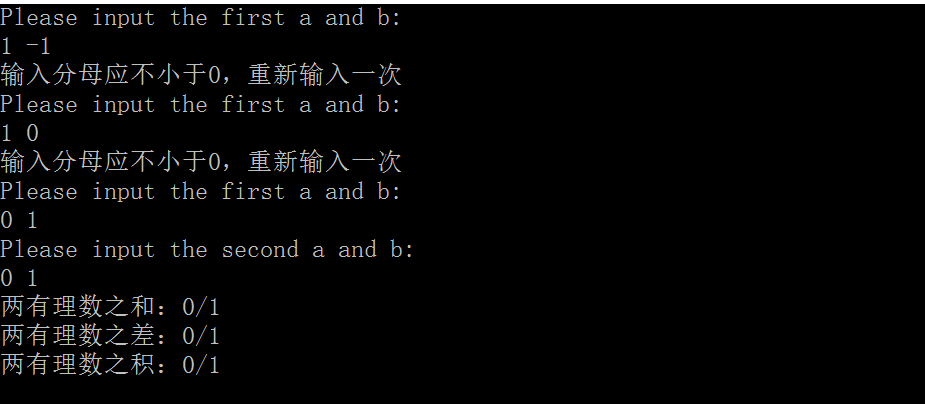
五.总结
- 数据结构包括数据对象和数据对象之间的联系
- 抽象数据类型是指一个数学模型以及定义在此数学模型上的一组操作。抽象数据类型需要通过已有的数据类型来实现。抽象数据类型是与表示无关的数据类型,是一个数据模型及定义在该模型上的一组运算。
- 通过做这类题目,我感觉我存在很大的不足,在开辟空间,释放空间上还是懵懵的



