分享stackexchange的一篇问答:https://stats.stackexchange.com/questions/11602/training-with-the-full-dataset-after-cross-validation
Q: Is it always a good idea to train with the full dataset after cross-validation? Put it another way, is it ok to train with all the samples in my dataset and not being able to check if this particular fittingoverfits?
A: The way to think of cross-validation is as estimating the performance obtained using a method for building a model, rather than for estimating the performance of a model.
If you use cross-validation to estimate the hyperparameters of a model and then use those hyper-parameters to fit a model to the whole dataset, then that is fine, provided that you recognise that the cross-validation estimate of performance is likely to be (possibly substantially) optimistically biased. This is because part of the model (the hyper-parameters) have been selected to minimise the cross-validation performance, so if the cross-validation statistic has a non-zero variance (and it will) there is the possibility of over-fitting the model selection criterion.
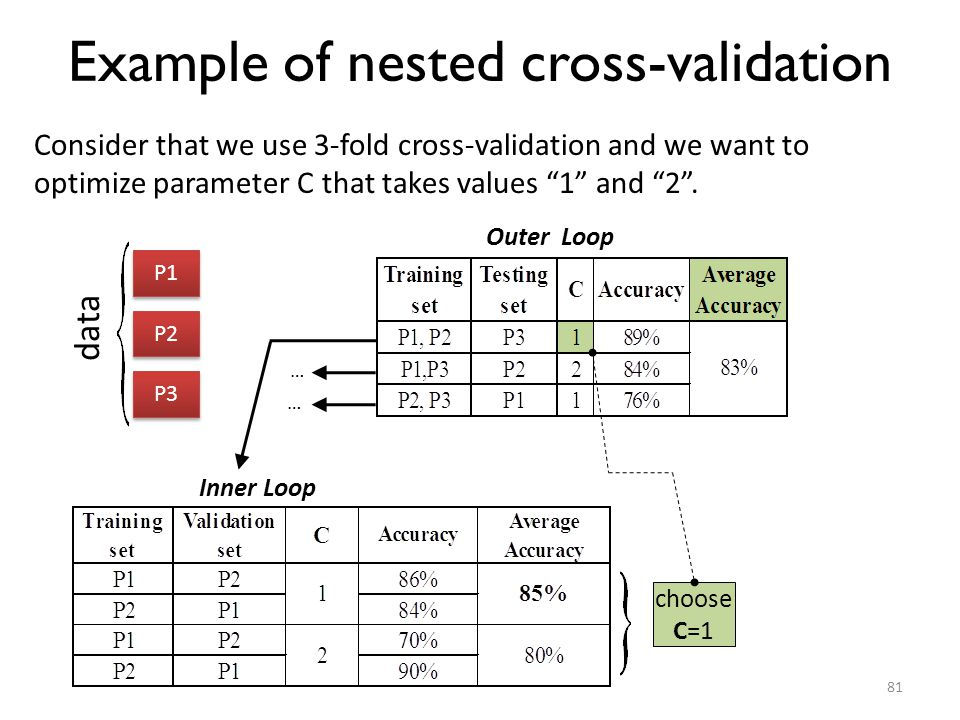
If you want to choose the hyper-parameters and estimate the performance of the resulting model then you need to perform a nested cross-validation, where the outer cross-validation is used to assess the performance of the model, and in each fold cross-validation is used to determine the hyper-parameters separately in each fold. You build the final model by using cross-validation on the whole set to choose the hyper-parameters and then build the classifier on the whole dataset using the optimized hyper-parameters.
This is of course computationally expensive, but worth it as the bias introduced by improper performance estimation can be large. See my paper
G. C. Cawley and N. L. C. Talbot, Over-fitting in model selection and subsequent selection bias in performance evaluation, Journal of Machine Learning Research, 2010. Research, vol. 11, pp. 2079-2107, July 2010. (www, pdf)
However, it is still possible to have over-fitting in model selection (nested cross-validation just allows you to test for it). A method I have found useful is to add a regularisation term to the cross-validation error that penalises hyper-parameter values likely to result in overly-complex models, see
G. C. Cawley and N. L. C. Talbot, Preventing over-fitting in model selection via Bayesian regularisation of the hyper-parameters, Journal of Machine Learning Research, volume 8, pages 841-861, April 2007. (www,pdf)
So the answers to your question are (i) yes, you should use the full dataset to produce your final model as the more data you use the more likely it is to generalise well but (ii) make sure you obtain an unbiased performance estimate via nested cross-validation and potentially consider penalising the cross-validation statistic to further avoid over-fitting in model selection.
交叉验证的目的可以理解为是为了估算建模方法的性能,而不是具体模型的性能。
如果使用交叉验证来选择超参数,那使用选取出的超参数在全部数据上拟合模型,这是对的。但是需要注意的是,使用这种交叉验证方法得出的性能估计是很有可能有偏差的。这是因为被选出模型的超参数是通过最小化交叉验证的性能而选出来的,这种情况下,交叉验证的性能用于衡量模型的泛化误差,不够准确。
如果既需要选择超参数,又需要估算选出模型的性能,可以选择Nested Cross-Validation。Nested Cross-Validation中的外层交叉验证用于估算模型性能,内层交叉验证用于选择超参数。最后,基于选出的超参数和全部数据集,产生最终的模型。
尽管这样,还是有可能在模型选择阶段存在过拟合(Nested Cross-Validation只是允许你可以对这种情况进行测试,如何测?)。一种解决方法是在cross-validation error中加入正则项,用于惩罚易产生过度复杂模型的超参数。
总结,(1)最终的模型应该使用全部数据集来建模,因为越多的数据,模型泛化能力越好;(2)需要确认性能估计得无偏的,Nested Cross-Validation和加惩罚项是解决性能估计出现偏差的方法。