LC 二叉搜索树-汇总
二叉搜索树
二叉搜索树又称二叉排序树,具有以下性质:
-
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
-
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
-
它的左右子树也分别为二叉搜索树
注意:二叉搜索树中序遍历的结果是有序的。
95. 不同的二叉搜索树 II
给你一个整数 n ,请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。
示例 1:
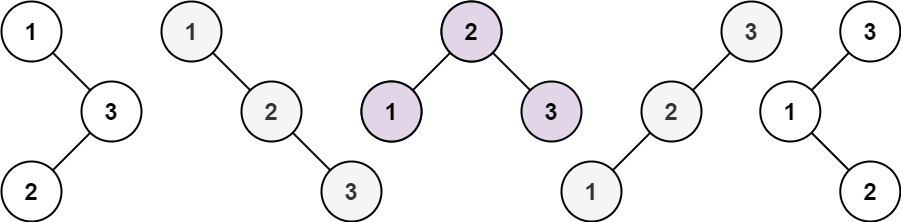
输入:n = 3
输出:[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]
示例 2:
输入:n = 1
输出:[[1]]
回溯
二叉搜索树关键的性质是根节点的值大于左子树所有节点的值,小于右子树所有节点的值,且左子树和右子树也同样为二叉搜索树。因此在生成所有可行的二叉搜索树的时候,假设当前序列长度为 n,如果枚举根节点的值为 i,那么根据二叉搜索树的性质可以知道左子树的节点值的集合为 \([1…i−1]\),右子树的节点值的集合为 \([i+1…n]\)。而左子树和右子树的生成相较于原问题是一个序列长度缩小的子问题,因此可以想到用回溯的方法来解决这道题目。
定义 generateTrees(start, end) 函数表示当前值的集合为 \([start,end]\),返回序列 \([start,end]\) 生成的所有可行的二叉搜索树。按照上文的思路,考虑枚举 \([start,end]\) 中的值 i 为当前二叉搜索树的根,那么序列划分为了 \([start,i−1]\) 和 \([i+1,end]\) 两部分。递归调用这两部分,即 generateTrees(start, i - 1) 和 generateTrees(i + 1, end),获得所有可行的左子树和可行的右子树,那么最后一步只要从可行左子树集合中选一棵,再从可行右子树集合中选一棵拼接到根节点上,并将生成的二叉搜索树放入答案数组即可。
递归的入口即为 generateTrees(1, n),出口为当 \(start>end\) 的时候,当前二叉搜索树为空,返回空节点即可,必须要返回空节点。
Java-代码🌳
class Solution {
public List<TreeNode> generateTrees(int n) {
if (n == 0) {
return new LinkedList<TreeNode>();
}
return generateTrees(1, n);
}
public List<TreeNode> generateTrees(int start, int end) {
List<TreeNode> allTrees = new LinkedList<TreeNode>();
if (start > end) {
allTrees.add(null); //!返回空节点,不能直接 return
return allTrees;
}
// 枚举可行根节点
for (int i = start; i <= end; i++) {
// 获得所有可行的左子树集合
List<TreeNode> leftTrees = generateTrees(start, i - 1);
// 获得所有可行的右子树集合
List<TreeNode> rightTrees = generateTrees(i + 1, end);
// 从左子树集合中选出一棵左子树,从右子树集合中选出一棵右子树,拼接到根节点上
for (TreeNode left : leftTrees) {
for (TreeNode right : rightTrees) {
TreeNode currTree = new TreeNode(i);
currTree.left = left;
currTree.right = right;
allTrees.add(currTree);
}
}
}
return allTrees;
}
}
C++-代码🌳
class Solution {
public:
vector<TreeNode*> generateTrees(int start, int end) {
if (start > end) {
return { nullptr };
}
vector<TreeNode*> allTrees;
// 枚举可行根节点
for (int i = start; i <= end; i++) {
// 获得所有可行的左子树集合
vector<TreeNode*> leftTrees = generateTrees(start, i - 1);
// 获得所有可行的右子树集合
vector<TreeNode*> rightTrees = generateTrees(i + 1, end);
// 从左子树集合中选出一棵左子树,从右子树集合中选出一棵右子树,拼接到根节点上
for (auto& left : leftTrees) {
for (auto& right : rightTrees) {
TreeNode* currTree = new TreeNode(i);
currTree->left = left;
currTree->right = right;
allTrees.emplace_back(currTree);
}
}
}
return allTrees;
}
vector<TreeNode*> generateTrees(int n) {
if (!n) {
return {};
}
return generateTrees(1, n);
}
};
复杂度分析
-
时间复杂度:整个算法的时间复杂度取决于「可行二叉搜索树的个数」,而对于 n 个点生成的二叉搜索树数量等价于数学上第 n 个「卡特兰数」,用 \(G_n\) 表示。卡特兰数具体的细节请自行查询。生成一棵二叉搜索树需要 \(O(n)\) 的时间复杂度,一共有 \(G_n\) 棵二叉搜索树,也就是 \(O(nG_n)\)。而卡特兰数以 \(\frac{4^n}{n^{3/2}}\) 增长,因此总时间复杂度为 \(O(\frac{4^n}{n^{1/2}})\)。
-
空间复杂度:n 个点生成的二叉搜索树有 \(G_n\) 棵,每棵有 n 个节点,因此存储的空间需要 \(O(nG_n) = O(\frac{4^n}{n^{1/2}})\),递归函数需要 \(O(n)\) 的栈空间,因此总空间复杂度为 \(O(\frac{4^n}{n^{1/2}})\)。
96. 不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的二叉搜索树有多少种?返回满足题意的二叉搜索树的种数。
注:直接用【95. 不同的二叉搜索树 II】解法,对结果 allTrees 取 size(),会超出时间限制。
动态规划
给定一个有序序列 \(1 \cdots n\),为了构建出一棵二叉搜索树,可以遍历每个数字 i,将该数字作为树根,将 \(1⋯(i−1)\) 序列作为左子树,将 \((i+1)⋯n\) 序列作为右子树。接着可以按照同样的方式递归构建左子树和右子树。
在上述构建的过程中,由于根的值不同,因此能保证每棵二叉搜索树是唯一的。
由此可见,原问题可以分解成规模较小的两个子问题,且子问题的解可以复用。因此,可以想到使用动态规划来求解本题。
题目要求是计算不同二叉搜索树的个数。为此,可以定义两个函数:
-
\(G(n)\): 长度为 n 的序列能构成的不同二叉搜索树的个数。
-
\(F(i,n)\): 以 i 为根、序列长度为 n 的不同二叉搜索树个数 \((1≤i≤n)\)。
因此有:
对于边界情况,当序列长度为 1(只有根)或为 0(空树)时,只有一种情况,即:
给定序列 \(1⋯n\),选择数字 i 作为根,则根为 i 的所有二叉搜索树的集合是左子树集合和右子树集合的笛卡尔积,对于笛卡尔积中的每个元素,加上根节点之后形成完整的二叉搜索树,如下图所示:
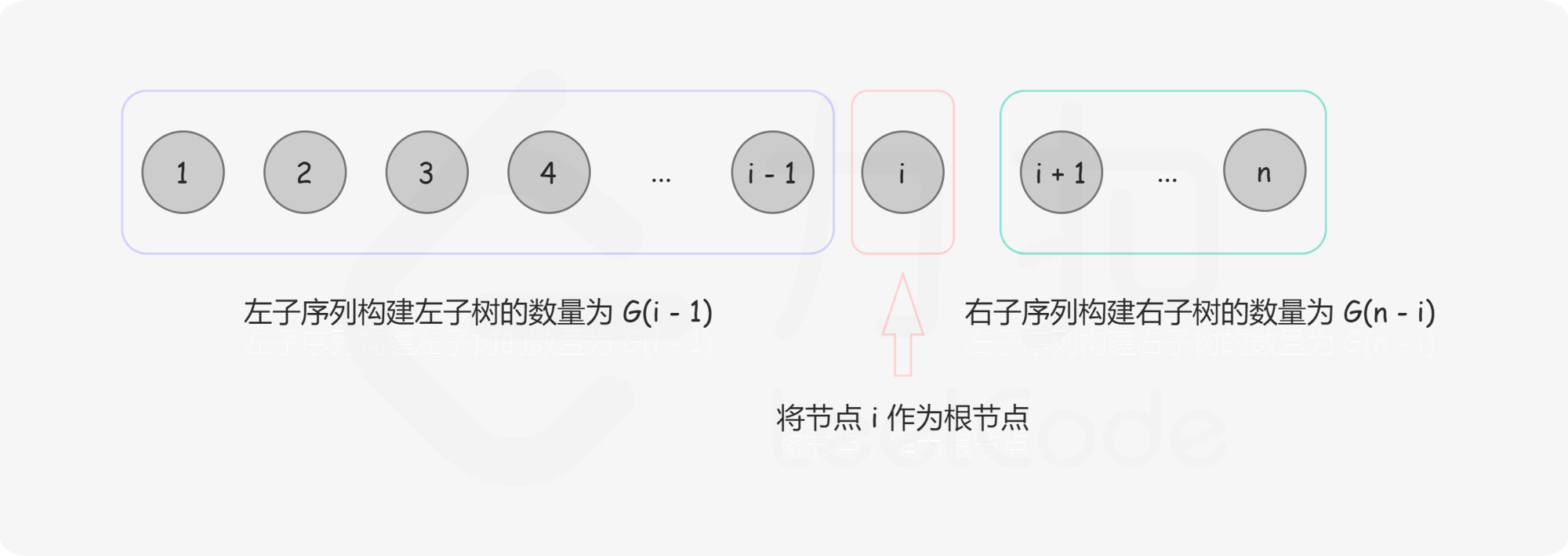
因此,
将上述两公式结合,可以得到 \(G(n)\) 的递归表达式:
至此,从小到大计算 G 函数即可,因为 \(G(n)\) 的值依赖于 \(G(0)⋯G(n−1)\)。
Java-代码🌳
class Solution {
public int numTrees(int n) {
int[] G = new int[n + 1];
G[0] = 1;
G[1] = 1;
for (int i = 2; i <= n; ++i) {
for (int j = 1; j <= i; ++j) {
G[i] += G[j - 1] * G[i - j];
}
}
return G[n];
}
}
C++-代码🌳
class Solution {
public:
int numTrees(int n) {
vector<int> G(n + 1, 0);
G[0] = 1;
G[1] = 1;
for (int i = 2; i <= n; ++i) {
for (int j = 1; j <= i; ++j) {
G[i] += G[j - 1] * G[i - j];
}
}
return G[n];
}
};
复杂度分析
-
时间复杂度 : \(O(n^2)\),其中 n 表示二叉搜索树的节点个数。\(OG(n)\) 函数一共有 n 个值需要求解,每次求解需要 \(O(n)\) 的时间复杂度,因此总时间复杂度为 \(O(n^2)\)。
-
空间复杂度 : \(O(n)\)。需要 \(O(n)\) 的空间存储 G 数组。
98. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效二叉搜索树定义如下:
-
节点的左子树只包含 小于 当前节点的数。
-
节点的右子树只包含 大于 当前节点的数。
-
所有左子树和右子树自身必须也是二叉搜索树。
1) 递归
二叉搜索树性质:如果该二叉树的左子树不为空,则左子树上所有节点的值均小于它的根节点的值; 若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值;它的左右子树也为二叉搜索树。
因此,可设计一个递归函数 helper(root, lower, upper) 来递归判断,函数表示考虑以 root 为根的子树,判断子树中所有节点的值是否都在 (l,r) 的范围内(注意是开区间)。如果 root 节点的值 val 不在 (l,r) 的范围内说明不满足条件直接返回,否则要继续递归调用检查它的左右子树是否满足,如果都满足才说明这是一棵二叉搜索树。
那么根据二叉搜索树的性质,在递归调用左子树时,需要把上界 upper 改为 root.val,即调用 helper(root.left, lower, root.val),因为左子树里所有节点的值均小于它的根节点的值。同理递归调用右子树时,需要把下界 lower 改为 root.val,即调用 helper(root.right, root.val, upper)。
函数递归调用的入口为 helper(root, -inf, +inf), inf 表示一个无穷大的值。
Java-代码🌳
class Solution {
public boolean isValidBST(TreeNode root) {
return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE);
}
public boolean isValidBST(TreeNode node, long lower, long upper) {
if (node == null) {
return true;
}
if (node.val <= lower || node.val >= upper) {
return false;
}
return isValidBST(node.left, lower, node.val) && isValidBST(node.right, node.val, upper);
}
}
C++-代码🌳
class Solution {
public:
bool helper(TreeNode* root, long long lower, long long upper) {
if (root == nullptr) {
return true;
}
if (root -> val <= lower || root -> val >= upper) {
return false;
}
return helper(root -> left, lower, root -> val) && helper(root -> right, root -> val, upper);
}
bool isValidBST(TreeNode* root) {
return helper(root, LONG_MIN, LONG_MAX);
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 n 为二叉树的节点个数。在递归调用的时候二叉树的每个节点最多被访问一次,因此时间复杂度为 \(O(n)\)。
-
空间复杂度:\(O(n)\),其中 n 为二叉树的节点个数。递归函数在递归过程中需要为每一层递归函数分配栈空间,所以这里需要额外的空间且该空间取决于递归的深度,即二叉树的高度。最坏情况下二叉树为一条链,树的高度为 n ,递归最深达到 n 层,故最坏情况下空间复杂度为 \(O(n)\)。
2) 中序遍历
二叉搜索树性质:如果该二叉树的左子树不为空,则左子树上所有节点的值均小于它的根节点的值; 若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值;它的左右子树也为二叉搜索树。
因此,可以进一步知道二叉搜索树「中序遍历」得到的值构成的序列一定是升序的,所以,在中序遍历的时候实时检查当前节点的值是否大于前一个中序遍历到的节点的值即可。如果均大于说明这个序列是升序的,整棵树是二叉搜索树,否则不是,使用栈来模拟中序遍历的过程。
Java-代码🌳
class Solution {
public boolean isValidBST(TreeNode root) {
Deque<TreeNode> stack = new LinkedList<TreeNode>();
double inorder = -Double.MAX_VALUE;
while (!stack.isEmpty() || root != null) {
while (root != null) {
stack.push(root);
root = root.left;
}
root = stack.pop();
// 如果中序遍历得到的节点的值小于等于前一个 inorder,说明不是二叉搜索树
if (root.val <= inorder) {
return false;
}
inorder = root.val;
root = root.right;
}
return true;
}
}
C++-代码🌳
class Solution {
public:
bool isValidBST(TreeNode* root) {
stack<TreeNode*> stack;
long long inorder = (long long)INT_MIN - 1;
while (!stack.empty() || root != nullptr) {
while (root != nullptr) {
stack.push(root);
root = root -> left;
}
root = stack.top();
stack.pop();
// 如果中序遍历得到的节点的值小于等于前一个 inorder,说明不是二叉搜索树
if (root -> val <= inorder) {
return false;
}
inorder = root -> val;
root = root -> right;
}
return true;
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 n 为二叉树的节点个数。二叉树的每个节点最多被访问一次,因此时间复杂度为 \(O(n)\)。
-
空间复杂度:\(O(n)\),其中 n 为二叉树的节点个数。栈最多存储 n 个节点,因此需要额外的 \(O(n)\) 的空间。
99. 恢复二叉搜索树
给你二叉搜索树的根节点 root ,该树中的恰好两个节点的值被错误地交换。请在不改变其结构的情况下,恢复这棵树。
示例 1:
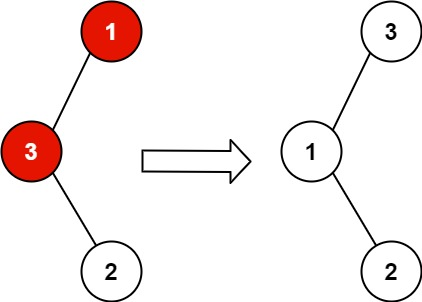
输入:root = [1,3,null,null,2]
输出:[3,1,null,null,2]
解释:3 不能是 1 的左孩子,因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。
示例 2:
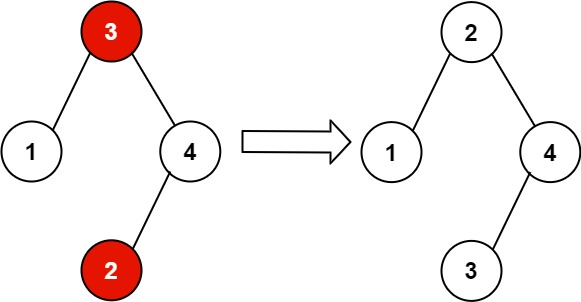
输入:root = [3,1,4,null,null,2]
输出:[2,1,4,null,null,3]
解释:2 不能在 3 的右子树中,因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。
提示:
-
树上节点的数目在范围
[2, 1000]内 -
\(-2^{31} <= Node.val <= 2^{31} - 1\)
1) 显式中序遍历
对于二叉搜索树,如果对其进行中序遍历,得到的值序列是递增有序的,而如果错误地交换了两个节点,等价于在这个值序列中交换了两个值,破坏了值序列的递增性。
假设有一个递增序列 \(a=[1,2,3,4,5,6,7]\)。如果交换两个不相邻的数字,例如 2 和 6,原序列变成了 \(a=[1,6,3,4,5,2,7]\),那么显然序列中有两个位置不满足 \(a_i<a_{i+1}\),在这个序列中体现为 \(6>3,5>2\),因此只要找到这两个位置,即可找到被错误交换的两个节点。如果交换两个相邻的数字,例如 2 和 3,此时交换后的序列只有一个位置不满足 \(a_i<a_{i+1}\) 。因此整个值序列中不满足条件的位置或者有两个,或者有一个。
因此,
-
找到二叉搜索树中序遍历得到值序列的不满足条件的位置。
-
如果有两个,记为 \(i\) 和 \(j\)(\(i<j\) 且 \(a_i>a_{i+1}\&\&\ a_j>a_{j+1})\),那么对应被错误交换的节点即为 \(a_i\) 对应的节点和 \(a_{j+1}\) 对应的节点,分别记为 x 和 y。
-
如果有一个,记为 \(i\),那么对应被错误交换的节点即为 \(a_i\) 对应的节点和 \(a_{i+1}\) 对应的节点,分别记为 x 和 y。
-
交换 x 和 y 两个节点即可。
实现:开辟一个新数组 nums 来记录中序遍历得到的值序列,然后线性遍历找到两个位置 i 和 j,并重新遍历原二叉搜索树修改对应节点的值完成修复。
Java-代码🌳
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public void recoverTree(TreeNode root) {
List<Integer> nums = new ArrayList<Integer>();
//中序遍历获得数组
inorder(root, nums);
//寻找逆序
int[] swapped = findTwoSwapped(nums);
recover(root, 2, swapped[0], swapped[1]);
}
public void inorder(TreeNode root, List<Integer> nums){
if(root==null){
return;
}
inorder(root.left, nums);
nums.add(root.val);
inorder(root.right, nums);
}
public int[] findTwoSwapped(List<Integer> nums){
int index1 = -1, index2 = -1;
int n = nums.size();
for(int i=0; i<n-1; i++){
if(nums.get(i+1) < nums.get(i)){
index2 = i+1;
if(index1 == -1){
index1 = i;
}else{
break;
}
}
}
int x = nums.get(index1), y = nums.get(index2); //返回值,而不是返回索引
return new int[]{x, y};
}
public void recover(TreeNode root, int count, int x, int y){
if(root==null){
return;
}
if(root.val == x || root.val == y){
root.val = root.val==x?y:x;
count--;
if(count==0){
return;
}
}
recover(root.left, count, x, y);
recover(root.right, count, x, y);
}
}
C++-代码🌳
class Solution {
public:
void inorder(TreeNode* root, vector<int>& nums) {
if (root == nullptr) {
return;
}
inorder(root->left, nums);
nums.push_back(root->val);
inorder(root->right, nums);
}
pair<int,int> findTwoSwapped(vector<int>& nums) {
int n = nums.size();
int index1 = -1, index2 = -1;
for (int i = 0; i < n - 1; ++i) {
if (nums[i + 1] < nums[i]) {
index2 = i + 1;
if (index1 == -1) {
index1 = i;
} else {
break;
}
}
}
int x = nums[index1], y = nums[index2];
return {x, y};
}
void recover(TreeNode* r, int count, int x, int y) {
if (r != nullptr) {
if (r->val == x || r->val == y) {
r->val = r->val == x ? y : x;
if (--count == 0) {
return;
}
}
recover(r->left, count, x, y);
recover(r->right, count, x, y);
}
}
void recoverTree(TreeNode* root) {
vector<int> nums;
inorder(root, nums);
pair<int,int> swapped= findTwoSwapped(nums);
recover(root, 2, swapped.first, swapped.second);
}
};
复杂度分析
-
时间复杂度:\(O(N)\),其中 N 为二叉搜索树的节点数。中序遍历需要 \(O(N)\) 的时间,判断两个交换节点在最好的情况下是 \(O(1)\),在最坏的情况下是 \(O(N)\),因此总时间复杂度为 \(O(N)\)。
-
空间复杂度:\(O(N)\)。需要用 \(nums\) 数组存储树的中序遍历列表。
2) 隐式中序遍历
方法一是显式地将中序遍历的值序列保存在一个 nums 数组中,然后再去寻找被错误交换的节点,也可以隐式地在中序遍历的过程就找到被错误交换的节点 x 和 y。
具体来说,由于只关心中序遍历的值序列中每个相邻的位置的大小关系是否满足条件,且错误交换后最多两个位置不满足条件,因此在中序遍历的过程只需要维护当前中序遍历到的最后一个节点 pred,然后在遍历到下一个节点的时候,看两个节点的值是否满足前者小于后者即可,如果不满足说明找到了一个交换的节点,且在找到两次以后就可以终止遍历。
这样就可以在中序遍历中直接找到被错误交换的两个节点 x 和 y,不用显式建立 nums 数组。
中序遍历的实现有迭代和递归两种等价的写法,此处使用迭代,需要手动维护栈。
Java-代码🌳
class Solution {
public void recoverTree(TreeNode root) {
Deque<TreeNode> stack = new ArrayDeque<TreeNode>();
TreeNode x = null, y = null, pred = null;
while (!stack.isEmpty() || root != null) {
while (root != null) {
stack.push(root);
root = root.left;
}
root = stack.pop();
if (pred != null && root.val < pred.val) {
y = root; //存储第二位逆序数
if (x == null) {
x = pred; //存储第一位逆序数
} else {
break;
}
}
pred = root; //保存前一个节点值
root = root.right;
}
swap(x, y);
}
public void swap(TreeNode x, TreeNode y) {
int tmp = x.val;
x.val = y.val;
y.val = tmp;
}
}
C++-代码🌳
class Solution {
public:
void recoverTree(TreeNode* root) {
stack<TreeNode*> stk;
TreeNode* x = nullptr;
TreeNode* y = nullptr;
TreeNode* pred = nullptr;
while (!stk.empty() || root != nullptr) {
while (root != nullptr) {
stk.push(root);
root = root->left;
}
root = stk.top();
stk.pop();
if (pred != nullptr && root->val < pred->val) {
y = root;
if (x == nullptr) {
x = pred;
}
else break;
}
pred = root;
root = root->right;
}
swap(x->val, y->val);
}
};
复杂度分析
- 时间复杂度:最坏情况下(即待交换节点为二叉搜索树最右侧的叶子节点)需要遍历整棵树,时间复杂度为 \(O(N)\),其中 \(N\) 为二叉搜索树的节点个数。
- 空间复杂度:\(O(H)\),其中 \(H\) 为二叉搜索树的高度。中序遍历的时候栈的深度取决于二叉搜索树的高度。
3) Morris 中序遍历
Morris 遍历算法,该算法能将非递归的中序遍历空间复杂度降为 O(1)。
Morris 遍历算法整体步骤如下(假设当前遍历到的节点为 x):
- 如果 x 无左孩子,则访问 x 的右孩子,即
x=x.right。 - 如果 x 有左孩子,则找到 x 左子树上最右的节点(即左子树中序遍历的最后一个节点,x 在中序遍历中的前驱节点),记为 predecessor。根据 predecessor 的右孩子是否为空,进行如下操作。
- 如果 predecessor 的右孩子为空,则将其右孩子指向 x,然后访问 x 的左孩子,即 x=x.left。
- 如果 predecessor 的右孩子不为空,则此时其右孩子指向 x,说明已经遍历完 x 的左子树,将 predecessor 的右孩子置空,然后访问 x 的右孩子,即 x=x.right。
- 重复上述操作,直至访问完整棵树。
其实整个过程就多做一步:将当前节点左子树中最右边的节点指向它,这样在左子树遍历完成后通过这个指向走回了 x,且能再通过这个知晓已经遍历完成了左子树,而不用再通过栈来维护,省去了栈的空间复杂度。其他地方与方法二并无不同。
Java-代码🌳
class Solution {
public void recoverTree(TreeNode root) {
TreeNode x = null, y = null, pred = null, predecessor = null;
while (root != null) {
if (root.left != null) {
// predecessor 节点就是当前 root 节点向左走一步,然后一直向右走至无法走为止
predecessor = root.left;
while (predecessor.right != null && predecessor.right != root) {
predecessor = predecessor.right;
}
// 让 predecessor 的右指针指向 root,继续遍历左子树
if (predecessor.right == null) {
predecessor.right = root;
root = root.left;
}
// 说明左子树已经访问完了,我们需要断开链接
else {
if (pred != null && root.val < pred.val) {
y = root;
if (x == null) {
x = pred;
}
}
pred = root;
predecessor.right = null;
root = root.right;
}
}
// 如果没有左孩子,则直接访问右孩子
else {
if (pred != null && root.val < pred.val) {
y = root;
if (x == null) {
x = pred;
}
}
pred = root;
root = root.right;
}
}
swap(x, y);
}
public void swap(TreeNode x, TreeNode y) {
int tmp = x.val;
x.val = y.val;
y.val = tmp;
}
}
C++-代码🌳
class Solution {
public:
void recoverTree(TreeNode* root) {
TreeNode *x = nullptr, *y = nullptr, *pred = nullptr, *predecessor = nullptr;
while (root != nullptr) {
if (root->left != nullptr) {
// predecessor 节点就是当前 root 节点向左走一步,然后一直向右走至无法走为止
predecessor = root->left;
while (predecessor->right != nullptr && predecessor->right != root) {
predecessor = predecessor->right;
}
// 让 predecessor 的右指针指向 root,继续遍历左子树
if (predecessor->right == nullptr) {
predecessor->right = root;
root = root->left;
}
// 说明左子树已经访问完了,我们需要断开链接
else {
if (pred != nullptr && root->val < pred->val) {
y = root;
if (x == nullptr) {
x = pred;
}
}
pred = root;
predecessor->right = nullptr;
root = root->right;
}
}
// 如果没有左孩子,则直接访问右孩子
else {
if (pred != nullptr && root->val < pred->val) {
y = root;
if (x == nullptr) {
x = pred;
}
}
pred = root;
root = root->right;
}
}
swap(x->val, y->val);
}
};
复杂度分析
- 时间复杂度:\(O(N)\),其中 \(N\) 为二叉搜索树的高度。Morris 遍历中每个节点会被访问两次,因此总时间复杂度为 \(O(2N)=O(N)\)。
- 空间复杂度:\(O(1)\)。
108. 将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按升序排列,请你将其转换为一棵高度平衡二叉搜索树。nums 按严格递增顺序排列。
高度平衡二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
前言
二叉搜索树的中序遍历是升序序列,题目要求高度平衡,选择中间数字作为二叉搜索树的根节点,这样分给左右子树的数字个数相同或只相差 1,可以使得树保持平衡。如果数组长度是奇数,则根节点的选择是唯一的,如果数组长度是偶数,则可以选择中间位置左边的数字作为根节点或者选择中间位置右边的数字作为根节点,选择不同的数字作为根节点则创建的平衡二叉搜索树也是不同的。
确定平衡二叉搜索树的根节点之后,其余的数字分别位于平衡二叉搜索树的左子树和右子树中,左子树和右子树分别也是平衡二叉搜索树,因此可以通过递归的方式创建平衡二叉搜索树。
中序遍历
三种根节点选择方案:
-
总是选择中间位置左边的数字作为根节点,则根节点的下标为 \(mid=(left+right)/2\),此处的除法为整数除法。
-
总是选择中间位置右边的数字作为根节点,则根节点的下标为 \(mid=(left+right+1)/2\),此处的除法为整数除法。
-
选择任意一个中间位置数字作为根节点,则根节点的下标为 \(mid=(left+right)/2\) 和 \(mid=(left+right+1)/2\) 两者中随机选择一个,此处的除法为整数除法。
Java-代码🌳
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return helper(nums, 0, nums.length - 1);
}
public TreeNode helper(int[] nums, int left, int right) {
if (left > right) {
return null;
}
// 总是选择中间位置左边的数字作为根节点
int mid = (left + right) / 2;
TreeNode root = new TreeNode(nums[mid]);
root.left = helper(nums, left, mid - 1);
root.right = helper(nums, mid + 1, right);
return root;
}
}
C++-代码🌳
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
return helper(nums, 0, nums.size() - 1);
}
TreeNode* helper(vector<int>& nums, int left, int right) {
if (left > right) {
return nullptr;
}
// 总是选择中间位置左边的数字作为根节点
int mid = (left + right) / 2;
TreeNode* root = new TreeNode(nums[mid]);
root->left = helper(nums, left, mid - 1);
root->right = helper(nums, mid + 1, right);
return root;
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 \(n\) 是数组的长度。每个数字只访问一次。
-
空间复杂度:\(O(logn)\),其中 \(n\) 是数组的长度。空间复杂度不考虑返回值,因此空间复杂度主要取决于递归栈的深度,递归栈的深度是 \(O(logn)\)。
109. 有序链表转换二叉搜索树
给定一个单链表的头节点 head ,其中的元素按升序排序,将其转换为高度平衡的二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点的左右两个子树的高度差不超过 1。
1) 分治
可以找出链表元素的中位数作为根节点的值。
这里对于中位数的定义为:如果链表中的元素个数为奇数,那么唯一的中间值为中位数;如果元素个数为偶数,那么唯二的中间值都可以作为中位数,而不是常规定义中二者的平均值。
设当前链表的左端点为 left,右端点 right,包含关系为「左闭右开」,即 left 包含在链表中而 right 不包含在链表中。希望快速地找出链表的中位数节点 mid。
为什么要设定「左闭右开」的关系?由于题目中给定的链表为单向链表,访问后继元素十分容易,但无法直接访问前驱元素。因此在找出链表的中位数节点 mid 之后,如果设定「左闭右开」的关系,就可以直接用 (left, mid) 以及 (mid.next, right) 来表示左右子树对应的列表了。并且,初始的列表也可以用 (head, null) 方便地进行表示,其中 null 表示空节点。
「快慢指针法」找出链表中位数节点。初始时,快指针 fast 和慢指针 slow 均指向链表的左端点 left。将快指针 fast 向右移动两次的同时,将慢指针 slow 向右移动一次,直到快指针到达边界(即快指针到达右端点或快指针的下一个节点是右端点)。此时,慢指针对应的元素就是中位数。
在找出了中位数节点之后,将其作为当前根节点的元素,并递归地构造其左侧部分的链表对应的左子树,以及右侧部分的链表对应的右子树。
Java-代码🌳
class Solution {
public TreeNode sortedListToBST(ListNode head) {
return buildTree(head, null);
}
public TreeNode buildTree(ListNode left, ListNode right) {
if (left == right) {
return null;
}
ListNode mid = getMedian(left, right);
TreeNode root = new TreeNode(mid.val);
root.left = buildTree(left, mid);
root.right = buildTree(mid.next, right);
return root;
}
public ListNode getMedian(ListNode left, ListNode right) {
ListNode fast = left;
ListNode slow = left;
while (fast != right && fast.next != right) {
fast = fast.next;
fast = fast.next;
slow = slow.next;
}
return slow;
}
}
C++-代码🌳
class Solution {
public:
ListNode* getMedian(ListNode* left, ListNode* right) {
ListNode* fast = left;
ListNode* slow = left;
while (fast != right && fast->next != right) {
fast = fast->next;
fast = fast->next;
slow = slow->next;
}
return slow;
}
TreeNode* buildTree(ListNode* left, ListNode* right) {
if (left == right) {
return nullptr;
}
ListNode* mid = getMedian(left, right);
TreeNode* root = new TreeNode(mid->val);
root->left = buildTree(left, mid);
root->right = buildTree(mid->next, right);
return root;
}
TreeNode* sortedListToBST(ListNode* head) {
return buildTree(head, nullptr);
}
};
复杂度分析
-
时间复杂度:\(O(nlogn)\),其中 \(n\) 是链表的长度。设长度为 \(n\) 的链表构造二叉搜索树的时间为 \(T(n)\),递推式为 \(T(n)=2⋅T(n/2)+O(n)\),根据主定理,\(T(n)=O(nlogn)\)。
-
空间复杂度:\(O(logn)\),这里只计算除了返回答案之外的空间。平衡二叉树的高度为 \(O(logn)\),即为递归过程中栈的最大深度,也就是需要的空间。
2) 分治 + 中序遍历优化
方法一的时间复杂度的瓶颈在于寻找中位数节点。由于构造出的二叉搜索树的中序遍历结果就是链表本身,因此可以将分治和中序遍历结合起来,减少时间复杂度。
具体地,设当前链表的左端点编号为left,右端点编号为 right,包含关系为「双闭」,即 left 和 right 均包含在链表中。链表节点的编号为 [0,n)。中序遍历的顺序是「左子树 - 根节点 - 右子树」,那么在分治的过程中,不用急着找出链表的中位数节点,而是使用一个占位节点,等到中序遍历到该节点时,再填充它的值。
可以通过计算编号范围来进行中序遍历:
-
中位数节点对应的编号为 mid=(left+right+1)/2;编号为 (left+right)/2 的节点同样也可以是中位数节点。
-
左右子树对应的编号范围分别为 [left,mid−1] 和 [mid+1,right]。
如果 left>right,那么遍历到的位置对应着一个空节点,否则对应着二叉搜索树中的一个节点。
这样一来,其实已经知道了这棵二叉搜索树的结构,并且题目给定了它的中序遍历结果,那么只要对其进行中序遍历,就可以还原出整棵二叉搜索树了。
Java-代码🌳
class Solution {
ListNode globalHead;
public TreeNode sortedListToBST(ListNode head) {
globalHead = head;
int length = getLength(head);
return buildTree(0, length - 1);
}
public int getLength(ListNode head) {
int ret = 0;
while (head != null) {
++ret;
head = head.next;
}
return ret;
}
public TreeNode buildTree(int left, int right) {
if (left > right) {
return null;
}
int mid = (left + right + 1) / 2;
TreeNode root = new TreeNode();
root.left = buildTree(left, mid - 1);
root.val = globalHead.val;
globalHead = globalHead.next;
root.right = buildTree(mid + 1, right);
return root;
}
}
C++-代码🌳
class Solution {
public:
int getLength(ListNode* head) {
int ret = 0;
for (; head != nullptr; ++ret, head = head->next);
return ret;
}
TreeNode* buildTree(ListNode*& head, int left, int right) {
if (left > right) {
return nullptr;
}
int mid = (left + right + 1) / 2;
TreeNode* root = new TreeNode();
root->left = buildTree(head, left, mid - 1);
root->val = head->val;
head = head->next;
root->right = buildTree(head, mid + 1, right);
return root;
}
TreeNode* sortedListToBST(ListNode* head) {
int length = getLength(head);
return buildTree(head, 0, length - 1);
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 \(n\) 是链表的长度。设长度为 \(n\) 的链表构造二叉搜索树的时间为 \(T(n)\),递推式为 \(T(n)=2⋅T(n/2)+O(1)\),根据主定理,\(T(n)=O(n)\)。
-
空间复杂度:\(O(logn)\),这里只计算除了返回答案之外的空间。平衡二叉树的高度为 \(O(logn)\),即为递归过程中栈的最大深度,也就是需要的空间。
173. 二叉搜索树迭代器
实现一个二叉搜索树迭代器类 BSTIterator ,表示一个按中序遍历二叉搜索树(BST)的迭代器:
-
BSTIterator(TreeNode root)初始化BSTIterator类的一个对象。BST 的根节点 root 会作为构造函数的一部分给出。指针应初始化为一个不存在于 BST 中的数字,且该数字小于 BST 中的任何元素。 -
boolean hasNext()如果向指针右侧遍历存在数字,则返回 true ;否则返回 false 。 -
int next()将指针向右移动,然后返回指针处的数字。
注意,指针初始化为一个不存在于 BST 中的数字,所以对 next() 的首次调用将返回 BST 中的最小元素。
你可以假设 next() 调用总是有效的,也就是说,当调用 next() 时,BST 的中序遍历中至少存在一个下一个数字。
1) 扁平化
原问题等价于对二叉搜索树进行中序遍历。
直接对二叉搜索树做一次完全的递归遍历,获取中序遍历的全部结果并保存在数组中。随后,利用得到的数组本身来实现迭代器。
Java-代码🌳
class BSTIterator {
private int idx;
private List<Integer> arr;
public BSTIterator(TreeNode root) {
idx = 0;
arr = new ArrayList<Integer>();
inorderTraversal(root, arr);
}
public int next() {
return arr.get(idx++);
}
public boolean hasNext() {
return idx < arr.size();
}
private void inorderTraversal(TreeNode root, List<Integer> arr) {
if (root == null) {
return;
}
inorderTraversal(root.left, arr);
arr.add(root.val);
inorderTraversal(root.right, arr);
}
}
C++-代码🌳
class BSTIterator {
private:
void inorder(TreeNode* root, vector<int>& res) {
if (!root) {
return;
}
inorder(root->left, res);
res.push_back(root->val);
inorder(root->right, res);
}
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
inorder(root, res);
return res;
}
vector<int> arr;
int idx;
public:
BSTIterator(TreeNode* root): idx(0), arr(inorderTraversal(root)) {}
int next() {
return arr[idx++];
}
bool hasNext() {
return (idx < arr.size());
}
};
复杂度分析
-
时间复杂度:初始化需要 \(O(n)\) 的时间,其中 \(n\) 为树中节点的数量。随后每次调用只需要 \(O(1)\) 的时间。
-
空间复杂度:\(O(n)\),因为需要保存中序遍历的全部结果。
2) 迭代🍓
利用栈数据结构,通过迭代的方式对二叉树做中序遍历。此时,无需预先计算出中序遍历的全部结果,只需要实时维护当前栈的情况即可。
Java-代码🌳
class BSTIterator {
private TreeNode cur;
private Deque<TreeNode> stack;
public BSTIterator(TreeNode root) {
cur = root;
stack = new LinkedList<TreeNode>();
}
public int next() {
while (cur != null) {
stack.push(cur);
cur = cur.left;
}
cur = stack.pop();
int ret = cur.val;
cur = cur.right;
return ret;
}
public boolean hasNext() {
return cur != null || !stack.isEmpty();
}
}
C++-代码🌳
class BSTIterator {
private:
TreeNode* cur;
stack<TreeNode*> stk;
public:
BSTIterator(TreeNode* root): cur(root) {}
int next() {
while (cur != nullptr) {
stk.push(cur);
cur = cur->left;
}
cur = stk.top();
stk.pop();
int ret = cur->val;
cur = cur->right;
return ret;
}
bool hasNext() {
return cur != nullptr || !stk.empty();
}
};
复杂度分析
-
时间复杂度:显然,初始化和调用
hasNext()都只需要O(1)的时间。每次调用next()函数最坏情况下需要O(n)的时间;但考虑到 n 次调用next()函数总共会遍历全部的 n 个节点,因此总的时间复杂度为O(n),因此单次调用平均下来的均摊复杂度为O(1)。 -
空间复杂度:
O(n),其中 n 是二叉树的节点数量。空间复杂度取决于栈深度,而栈深度在二叉树为一条链的情况下会达到O(n)的级别。
230. 二叉搜索树中第K小的元素
给定一个二叉搜索树的根节点 root ,和一个整数 k ,请你设计一个算法查找其中第 k 个最小元素(从 1 开始计数)。
示例 1:
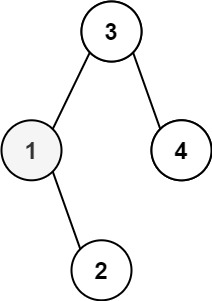
输入:root = [3,1,4,null,2], k = 1
输出:1
1) 中序遍历
通过中序遍历找到第 k 个最小元素。
Java-代码🌳
class Solution {
public int kthSmallest(TreeNode root, int k) {
Deque<TreeNode> stack = new ArrayDeque<TreeNode>();
while (root != null || !stack.isEmpty()) {
while (root != null) {
stack.push(root);
root = root.left;
}
root = stack.pop();
--k;
if (k == 0) {
break;
}
root = root.right;
}
return root.val;
}
}
C++-代码🌳
class Solution {
public:
int kthSmallest(TreeNode* root, int k) {
stack<TreeNode *> stack;
while (root != nullptr || stack.size() > 0) {
while (root != nullptr) {
stack.push(root);
root = root->left;
}
root = stack.top();
stack.pop();
--k;
if (k == 0) {
break;
}
root = root->right;
}
return root->val;
}
};
复杂度分析
-
时间复杂度:\(O(H+k)\),其中 H 是树的高度。在开始遍历之前,需要 \(O(H)\) 到达叶结点。当树是平衡树时,时间复杂度取得最小值 \(O(logN+k)\);当树是线性树(树中每个结点都只有一个子结点或没有子结点)时,时间复杂度取得最大值 \(O(N+k)\)。
-
空间复杂度:\(O(H)\),栈中最多需要存储 \(H\) 个元素。当树是平衡树时,空间复杂度取得最小值 \(O(logN)\);当树是线性树时,空间复杂度取得最大值 \(O(N)\)。
2) 记录子树的结点数
如果需要频繁地查找第 k 小的值,将如何优化算法?
在方法一中,之所以需要中序遍历前 k 个元素,是因为不知道子树的结点数量,不得不通过遍历子树的方式来获知。
因此,可以记录下以每个结点为根结点的子树的结点数,并在查找第 k 小的值时,使用如下方法搜索:
-
令 node 等于根结点,开始搜索。
-
对当前结点 node 进行如下操作:
-
如果 node 的左子树的结点数 left 小于 k−1,则第 k 小的元素一定在 node 的右子树中,令 node 等于其的右子结点,k 等于 k−left−1,并继续搜索;
-
如果 node 的左子树的结点数 left 等于 k−1,则第 k 小的元素即为 node ,结束搜索并返回 node 即可;
-
如果 node 的左子树的结点数 left 大于 k−1,则第 k 小的元素一定在 node 的左子树中,令 node 等于其左子结点,并继续搜索。
-
在实现中,既可以将以每个结点为根结点的子树的结点数存储在结点中,也可以将其记录在哈希表中。
Java-代码🌳
class Solution {
public int kthSmallest(TreeNode root, int k) {
MyBst bst = new MyBst(root);
return bst.kthSmallest(k);
}
}
class MyBst {
TreeNode root;
Map<TreeNode, Integer> nodeNum;
public MyBst(TreeNode root) {
this.root = root;
this.nodeNum = new HashMap<TreeNode, Integer>();
countNodeNum(root);
}
// 返回二叉搜索树中第k小的元素
public int kthSmallest(int k) {
TreeNode node = root;
while (node != null) {
int left = getNodeNum(node.left);
if (left < k - 1) {
node = node.right;
k -= left + 1;
} else if (left == k - 1) {
break;
} else {
node = node.left;
}
}
return node.val;
}
// 统计以node为根结点的子树的结点数
private int countNodeNum(TreeNode node) {
if (node == null) {
return 0;
}
nodeNum.put(node, 1 + countNodeNum(node.left) + countNodeNum(node.right));
return nodeNum.get(node);
}
// 获取以node为根结点的子树的结点数
private int getNodeNum(TreeNode node) {
return nodeNum.getOrDefault(node, 0);
}
}
C++-代码🌳
class MyBst {
public:
MyBst(TreeNode *root) {
this->root = root;
countNodeNum(root);
}
// 返回二叉搜索树中第k小的元素
int kthSmallest(int k) {
TreeNode *node = root;
while (node != nullptr) {
int left = getNodeNum(node->left);
if (left < k - 1) {
node = node->right;
k -= left + 1;
} else if (left == k - 1) {
break;
} else {
node = node->left;
}
}
return node->val;
}
private:
TreeNode *root;
unordered_map<TreeNode *, int> nodeNum;
// 统计以node为根结点的子树的结点数
int countNodeNum(TreeNode * node) {
if (node == nullptr) {
return 0;
}
nodeNum[node] = 1 + countNodeNum(node->left) + countNodeNum(node->right);
return nodeNum[node];
}
// 获取以node为根结点的子树的结点数
int getNodeNum(TreeNode * node) {
if (node != nullptr && nodeNum.count(node)) {
return nodeNum[node];
}else{
return 0;
}
}
};
class Solution {
public:
int kthSmallest(TreeNode* root, int k) {
MyBst bst(root);
return bst.kthSmallest(k);
}
};
复杂度分析
-
时间复杂度:预处理的时间复杂度为 \(O(N)\),其中 \(N\) 是树中结点的总数;需要遍历树中所有结点来统计以每个结点为根结点的子树的结点数。搜索的时间复杂度为 \(O(H)\),其中 \(H\) 是树的高度;当树是平衡树时,时间复杂度取得最小值 \(O(logN)\);当树是线性树时,时间复杂度取得最大值 \(O(N)\)。
-
空间复杂度:\(O(N)\),用于存储以每个结点为根结点的子树的结点数。
3) 平衡二叉搜索树
如果二叉搜索树经常被修改(插入/删除操作)并且你需要频繁地查找第 k 小的值,你将如何优化算法?
平衡二叉搜索树(AVL树)具有如下性质:
-
平衡二叉搜索树中每个结点的左子树和右子树的高度最多相差 1;
-
平衡二叉搜索树的子树也是平衡二叉搜索树;
-
一棵存有 n 个结点的平衡二叉搜索树的高度是 O(logn)。
在方法二中搜索二叉搜索树的时间复杂度为 O(H),其中 H 是树的高度;当树是平衡树时,时间复杂度取得最小值 O(logN)。因此,在记录子树的结点数的基础上,将二叉搜索树转换为平衡二叉搜索树,并在插入和删除操作中维护它的平衡状态(通过旋转和重组实现)。
Java-代码🌳
class Solution {
public int kthSmallest(TreeNode root, int k) {
// 中序遍历生成数值列表
List<Integer> inorderList = new ArrayList<Integer>();
inorder(root, inorderList);
// 构造平衡二叉搜索树
AVL avl = new AVL(inorderList);
// 模拟1000次插入和删除操作
int[] randomNums = new int[1000];
Random random = new Random();
for (int i = 0; i < 1000; ++i) {
randomNums[i] = random.nextInt(10001);
avl.insert(randomNums[i]);
}
shuffle(randomNums); // 列表乱序
for (int i = 0; i < 1000; ++i) {
avl.delete(randomNums[i]);
}
return avl.kthSmallest(k);
}
private void inorder(TreeNode node, List<Integer> inorderList) {
if (node.left != null) {
inorder(node.left, inorderList);
}
inorderList.add(node.val);
if (node.right != null) {
inorder(node.right, inorderList);
}
}
private void shuffle(int[] arr) {
Random random = new Random();
int length = arr.length;
for (int i = 0; i < length; i++) {
int randIndex = random.nextInt(length);
int temp = arr[i];
arr[i] = arr[randIndex];
arr[randIndex] = temp;
}
}
}
// 平衡二叉搜索树(AVL树):允许重复值
class AVL {
Node root;
// 平衡二叉搜索树结点
class Node {
int val;
Node parent;
Node left;
Node right;
int size;
int height;
public Node(int val) {
this(val, null);
}
public Node(int val, Node parent) {
this(val, parent, null, null);
}
public Node(int val, Node parent, Node left, Node right) {
this.val = val;
this.parent = parent;
this.left = left;
this.right = right;
this.height = 0; // 结点高度:以node为根节点的子树的高度(高度定义:叶结点的高度是0)
this.size = 1; // 结点元素数:以node为根节点的子树的节点总数
}
}
public AVL(List<Integer> vals) {
if (vals != null) {
this.root = build(vals, 0, vals.size() - 1, null);
}
}
// 根据vals[l:r]构造平衡二叉搜索树 -> 返回根结点
private Node build(List<Integer> vals, int l, int r, Node parent) {
int m = (l + r) >> 1;
Node node = new Node(vals.get(m), parent);
if (l <= m - 1) {
node.left = build(vals, l, m - 1, node);
}
if (m + 1 <= r) {
node.right = build(vals, m + 1, r, node);
}
recompute(node);
return node;
}
// 返回二叉搜索树中第k小的元素
public int kthSmallest(int k) {
Node node = root;
while (node != null) {
int left = getSize(node.left);
if (left < k - 1) {
node = node.right;
k -= left + 1;
} else if (left == k - 1) {
break;
} else {
node = node.left;
}
}
return node.val;
}
public void insert(int v) {
if (root == null) {
root = new Node(v);
} else {
// 计算新结点的添加位置
Node node = subtreeSearch(root, v);
boolean isAddLeft = v <= node.val; // 是否将新结点添加到node的左子结点
if (node.val == v) { // 如果值为v的结点已存在
if (node.left != null) { // 值为v的结点存在左子结点,则添加到其左子树的最右侧
node = subtreeLast(node.left);
isAddLeft = false;
} else { // 值为v的结点不存在左子结点,则添加到其左子结点
isAddLeft = true;
}
}
// 添加新结点
Node leaf = new Node(v, node);
if (isAddLeft) {
node.left = leaf;
} else {
node.right = leaf;
}
rebalance(leaf);
}
}
// 删除值为v的结点 -> 返回是否成功删除结点
public boolean delete(int v) {
if (root == null) {
return false;
}
Node node = subtreeSearch(root, v);
if (node.val != v) { // 没有找到需要删除的结点
return false;
}
// 处理当前结点既有左子树也有右子树的情况
// 若左子树比右子树高度低,则将当前结点替换为右子树最左侧的结点,并移除右子树最左侧的结点
// 若右子树比左子树高度低,则将当前结点替换为左子树最右侧的结点,并移除左子树最右侧的结点
if (node.left != null && node.right != null) {
Node replacement = null;
if (node.left.height <= node.right.height) {
replacement = subtreeFirst(node.right);
} else {
replacement = subtreeLast(node.left);
}
node.val = replacement.val;
node = replacement;
}
Node parent = node.parent;
delete(node);
rebalance(parent);
return true;
}
// 删除结点p并用它的子结点代替它,结点p至多只能有1个子结点
private void delete(Node node) {
if (node.left != null && node.right != null) {
return;
// throw new Exception("Node has two children");
}
Node child = node.left != null ? node.left : node.right;
if (child != null) {
child.parent = node.parent;
}
if (node == root) {
root = child;
} else {
Node parent = node.parent;
if (node == parent.left) {
parent.left = child;
} else {
parent.right = child;
}
}
node.parent = node;
}
// 在以node为根结点的子树中搜索值为v的结点,如果没有值为v的结点,则返回值为v的结点应该在的位置的父结点
private Node subtreeSearch(Node node, int v) {
if (node.val < v && node.right != null) {
return subtreeSearch(node.right, v);
} else if (node.val > v && node.left != null) {
return subtreeSearch(node.left, v);
} else {
return node;
}
}
// 重新计算node结点的高度和元素数
private void recompute(Node node) {
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
node.size = 1 + getSize(node.left) + getSize(node.right);
}
// 从node结点开始(含node结点)逐个向上重新平衡二叉树,并更新结点高度和元素数
private void rebalance(Node node) {
while (node != null) {
int oldHeight = node.height, oldSize = node.size;
if (!isBalanced(node)) {
node = restructure(tallGrandchild(node));
recompute(node.left);
recompute(node.right);
}
recompute(node);
if (node.height == oldHeight && node.size == oldSize) {
node = null; // 如果结点高度和元素数都没有变化则不需要再继续向上调整
} else {
node = node.parent;
}
}
}
// 判断node结点是否平衡
private boolean isBalanced(Node node) {
return Math.abs(getHeight(node.left) - getHeight(node.right)) <= 1;
}
// 获取node结点更高的子树
private Node tallChild(Node node) {
if (getHeight(node.left) > getHeight(node.right)) {
return node.left;
} else {
return node.right;
}
}
// 获取node结点更高的子树中的更高的子树
private Node tallGrandchild(Node node) {
Node child = tallChild(node);
return tallChild(child);
}
// 重新连接父结点和子结点(子结点允许为空)
private static void relink(Node parent, Node child, boolean isLeft) {
if (isLeft) {
parent.left = child;
} else {
parent.right = child;
}
if (child != null) {
child.parent = parent;
}
}
// 旋转操作
private void rotate(Node node) {
Node parent = node.parent;
Node grandparent = parent.parent;
if (grandparent == null) {
root = node;
node.parent = null;
} else {
relink(grandparent, node, parent == grandparent.left);
}
if (node == parent.left) {
relink(parent, node.right, true);
relink(node, parent, false);
} else {
relink(parent, node.left, false);
relink(node, parent, true);
}
}
// trinode操作
private Node restructure(Node node) {
Node parent = node.parent;
Node grandparent = parent.parent;
if ((node == parent.right) == (parent == grandparent.right)) { // 处理需要一次旋转的情况
rotate(parent);
return parent;
} else { // 处理需要两次旋转的情况:第1次旋转后即成为需要一次旋转的情况
rotate(node);
rotate(node);
return node;
}
}
// 返回以node为根结点的子树的第1个元素
private static Node subtreeFirst(Node node) {
while (node.left != null) {
node = node.left;
}
return node;
}
// 返回以node为根结点的子树的最后1个元素
private static Node subtreeLast(Node node) {
while (node.right != null) {
node = node.right;
}
return node;
}
// 获取以node为根结点的子树的高度
private static int getHeight(Node node) {
return node != null ? node.height : 0;
}
// 获取以node为根结点的子树的结点数
private static int getSize(Node node) {
return node != null ? node.size : 0;
}
}
C++-代码🌳
// 平衡二叉搜索树结点
struct Node {
int val;
Node * parent;
Node * left;
Node * right;
int size;
int height;
Node(int val) {
this->val = val;
this->parent = nullptr;
this->left = nullptr;
this->right = nullptr;
this->height = 0; // 结点高度:以node为根节点的子树的高度(高度定义:叶结点的高度是0)
this->size = 1; // 结点元素数:以node为根节点的子树的节点总数
}
Node(int val, Node * parent) {
this->val = val;
this->parent = parent;
this->left = nullptr;
this->right = nullptr;
this->height = 0; // 结点高度:以node为根节点的子树的高度(高度定义:叶结点的高度是0)
this->size = 1; // 结点元素数:以node为根节点的子树的节点总数
}
Node(int val, Node * parent, Node * left, Node * right) {
this->val = val;
this->parent = parent;
this->left = left;
this->right = right;
this->height = 0; // 结点高度:以node为根节点的子树的高度(高度定义:叶结点的高度是0)
this->size = 1; // 结点元素数:以node为根节点的子树的节点总数
}
};
// 平衡二叉搜索树(AVL树):允许重复值
class AVL {
public:
AVL(vector<int> & vals) {
if (!vals.empty()) {
root = build(vals, 0, vals.size() - 1, nullptr);
}
}
// 根据vals[l:r]构造平衡二叉搜索树 -> 返回根结点
Node * build(vector<int> & vals, int l, int r, Node * parent) {
int m = (l + r) >> 1;
Node * node = new Node(vals[m], parent);
if (l <= m - 1) {
node->left = build(vals, l, m - 1, node);
}
if (m + 1 <= r) {
node->right = build(vals, m + 1, r, node);
}
recompute(node);
return node;
}
// 返回二叉搜索树中第k小的元素
int kthSmallest(int k) {
Node * node = root;
while (node != nullptr) {
int left = getSize(node->left);
if (left < k - 1) {
node = node->right;
k -= left + 1;
} else if (left == k - 1) {
break;
} else {
node = node->left;
}
}
return node->val;
}
void insert(int v) {
if (root == nullptr) {
root = new Node(v);
} else {
// 计算新结点的添加位置
Node * node = subtreeSearch(root, v);
bool isAddLeft = v <= node->val; // 是否将新结点添加到node的左子结点
if (node->val == v) { // 如果值为v的结点已存在
if (node->left != nullptr) { // 值为v的结点存在左子结点,则添加到其左子树的最右侧
node = subtreeLast(node->left);
isAddLeft = false;
} else { // 值为v的结点不存在左子结点,则添加到其左子结点
isAddLeft = true;
}
}
// 添加新结点
Node * leaf = new Node(v, node);
if (isAddLeft) {
node->left = leaf;
} else {
node->right = leaf;
}
rebalance(leaf);
}
}
// 删除值为v的结点 -> 返回是否成功删除结点
bool Delete(int v) {
if (root == nullptr) {
return false;
}
Node * node = subtreeSearch(root, v);
if (node->val != v) { // 没有找到需要删除的结点
return false;
}
// 处理当前结点既有左子树也有右子树的情况
// 若左子树比右子树高度低,则将当前结点替换为右子树最左侧的结点,并移除右子树最左侧的结点
// 若右子树比左子树高度低,则将当前结点替换为左子树最右侧的结点,并移除左子树最右侧的结点
if (node->left != nullptr && node->right != nullptr) {
Node * replacement = nullptr;
if (node->left->height <= node->right->height) {
replacement = subtreeFirst(node->right);
} else {
replacement = subtreeLast(node->left);
}
node->val = replacement->val;
node = replacement;
}
Node * parent = node->parent;
Delete(node);
rebalance(parent);
return true;
}
private:
Node * root;
// 删除结点p并用它的子结点代替它,结点p至多只能有1个子结点
void Delete(Node * node) {
if (node->left != nullptr && node->right != nullptr) {
return;
// throw new Exception("Node has two children");
}
Node * child = node->left != nullptr ? node->left : node->right;
if (child != nullptr) {
child->parent = node->parent;
}
if (node == root) {
root = child;
} else {
Node * parent = node->parent;
if (node == parent->left) {
parent->left = child;
} else {
parent->right = child;
}
}
node->parent = node;
}
// 在以node为根结点的子树中搜索值为v的结点,如果没有值为v的结点,则返回值为v的结点应该在的位置的父结点
Node * subtreeSearch(Node * node, int v) {
if (node->val < v && node->right != nullptr) {
return subtreeSearch(node->right, v);
} else if (node->val > v && node->left != nullptr) {
return subtreeSearch(node->left, v);
} else {
return node;
}
}
// 重新计算node结点的高度和元素数
void recompute(Node * node) {
node->height = 1 + max(getHeight(node->left), getHeight(node->right));
node->size = 1 + getSize(node->left) + getSize(node->right);
}
// 从node结点开始(含node结点)逐个向上重新平衡二叉树,并更新结点高度和元素数
void rebalance(Node * node) {
while (node != nullptr) {
int oldHeight = node->height, oldSize = node->size;
if (!isBalanced(node)) {
node = restructure(tallGrandchild(node));
recompute(node->left);
recompute(node->right);
}
recompute(node);
if (node->height == oldHeight && node->size == oldSize) {
node = nullptr; // 如果结点高度和元素数都没有变化则不需要再继续向上调整
} else {
node = node->parent;
}
}
}
// 判断node结点是否平衡
bool isBalanced(Node * node) {
return abs(getHeight(node->left) - getHeight(node->right)) <= 1;
}
// 获取node结点更高的子树
Node * tallChild(Node * node) {
if (getHeight(node->left) > getHeight(node->right)) {
return node->left;
} else {
return node->right;
}
}
// 获取node结点更高的子树中的更高的子树
Node * tallGrandchild(Node * node) {
Node * child = tallChild(node);
return tallChild(child);
}
// 重新连接父结点和子结点(子结点允许为空)
static void relink(Node * parent, Node * child, bool isLeft) {
if (isLeft) {
parent->left = child;
} else {
parent->right = child;
}
if (child != nullptr) {
child->parent = parent;
}
}
// 旋转操作
void rotate(Node * node) {
Node * parent = node->parent;
Node * grandparent = parent->parent;
if (grandparent == nullptr) {
root = node;
node->parent = nullptr;
} else {
relink(grandparent, node, parent == grandparent->left);
}
if (node == parent->left) {
relink(parent, node->right, true);
relink(node, parent, false);
} else {
relink(parent, node->left, false);
relink(node, parent, true);
}
}
// trinode操作
Node * restructure(Node * node) {
Node * parent = node->parent;
Node * grandparent = parent->parent;
if ((node == parent->right) == (parent == grandparent->right)) { // 处理需要一次旋转的情况
rotate(parent);
return parent;
} else { // 处理需要两次旋转的情况:第1次旋转后即成为需要一次旋转的情况
rotate(node);
rotate(node);
return node;
}
}
// 返回以node为根结点的子树的第1个元素
static Node * subtreeFirst(Node * node) {
while (node->left != nullptr) {
node = node->left;
}
return node;
}
// 返回以node为根结点的子树的最后1个元素
static Node * subtreeLast(Node * node) {
while (node->right != nullptr) {
node = node->right;
}
return node;
}
// 获取以node为根结点的子树的高度
static int getHeight(Node * node) {
return node != nullptr ? node->height : 0;
}
// 获取以node为根结点的子树的结点数
static int getSize(Node * node) {
return node != nullptr ? node->size : 0;
}
};
class Solution {
public:
int kthSmallest(TreeNode * root, int k) {
// 中序遍历生成数值列表
vector<int> inorderList;
inorder(root, inorderList);
// 构造平衡二叉搜索树
AVL avl(inorderList);
// 模拟1000次插入和删除操作
vector<int> randomNums(1000);
std::random_device rd;
for (int i = 0; i < 1000; ++i) {
randomNums[i] = rd()%(10001);
avl.insert(randomNums[i]);
}
shuffle(randomNums); // 列表乱序
for (int i = 0; i < 1000; ++i) {
avl.Delete(randomNums[i]);
}
return avl.kthSmallest(k);
}
private:
void inorder(TreeNode * node, vector<int> & inorderList) {
if (node->left != nullptr) {
inorder(node->left, inorderList);
}
inorderList.push_back(node->val);
if (node->right != nullptr) {
inorder(node->right, inorderList);
}
}
void shuffle(vector<int> & arr) {
std::random_device rd;
int length = arr.size();
for (int i = 0; i < length; i++) {
int randIndex = rd()%length;
swap(arr[i],arr[randIndex]);
}
}
};
复杂度分析
-
时间复杂度:预处理的时间复杂度为 \(O(N)\),其中 \(N\) 是树中结点的总数。插入、删除和搜索的时间复杂度均为 \(O(logN)\)。
-
空间复杂度:\(O(N)\),用于存储平衡二叉搜索树。
235. 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
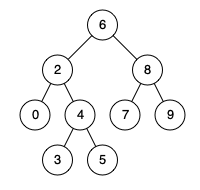
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
-
所有节点的值都是唯一的。
-
p、q 为不同节点且均存在于给定的二叉搜索树中。
1) 两次遍历
注意到题目中给出的是一棵「二叉搜索树」,因此可以快速地找出树中的某个节点以及从根节点到该节点的路径,例如需要找到节点 p:
-
从根节点开始遍历;
-
如果当前节点就是 p,那么成功地找到了节点;
-
如果当前节点的值大于 p 的值,说明 p 应该在当前节点的左子树,因此将当前节点移动到它的左子节点;
-
如果当前节点的值小于 p 的值,说明 p 应该在当前节点的右子树,因此将当前节点移动到它的右子节点。
对于节点 q 同理。在寻找节点的过程中,可以顺便记录经过的节点,这样就得到了从根节点到被寻找节点的路径。
当分别得到了从根节点到 p 和 q 的路径之后,就可以很方便地找到它们的最近公共祖先了。显然,p 和 q 的最近公共祖先就是从根节点到它们路径上的「分岔点」,也就是最后一个相同的节点。因此,如果设从根节点到 p 的路径为数组 path_p,从根节点到 q 的路径为数组 path_q,那么只要找出最大的编号 i,其满足 path_p[i]=path_q[i],那么对应的节点就是「分岔点」,即 p 和 q 的最近公共祖先就是 path_p[i](或 path_q[i])。
Java-代码🌳
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
List<TreeNode> path_p = getPath(root, p);
List<TreeNode> path_q = getPath(root, q);
TreeNode ancestor = null;
for (int i = 0; i < path_p.size() && i < path_q.size(); ++i) {
if (path_p.get(i) == path_q.get(i)) {
ancestor = path_p.get(i);
} else {
break;
}
}
return ancestor;
}
public List<TreeNode> getPath(TreeNode root, TreeNode target) {
List<TreeNode> path = new ArrayList<TreeNode>();
TreeNode node = root;
while (node != target) {
path.add(node);
if (target.val < node.val) {
node = node.left;
} else {
node = node.right;
}
}
path.add(node);
return path;
}
}
C++-代码🌳
class Solution {
public:
vector<TreeNode*> getPath(TreeNode* root, TreeNode* target) {
vector<TreeNode*> path;
TreeNode* node = root;
while (node != target) {
path.push_back(node);
if (target->val < node->val) {
node = node->left;
}
else {
node = node->right;
}
}
path.push_back(node);
return path;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
vector<TreeNode*> path_p = getPath(root, p);
vector<TreeNode*> path_q = getPath(root, q);
TreeNode* ancestor;
for (int i = 0; i < path_p.size() && i < path_q.size(); ++i) {
if (path_p[i] == path_q[i]) {
ancestor = path_p[i];
}
else {
break;
}
}
return ancestor;
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 \(n\) 是给定的二叉搜索树中的节点个数。上述代码需要的时间与节点 \(p\) 和 \(q\) 在树中的深度线性相关,而在最坏的情况下,树呈现链式结构,\(p\) 和 \(q\) 一个是树的唯一叶子结点,一个是该叶子结点的父节点,此时时间复杂度为 \(\Theta(n)\)。
-
空间复杂度:\(O(n)\),需要存储根节点到 \(p\) 和 \(q\) 的路径。和上面的分析方法相同,在最坏的情况下,路径的长度为 \(Θ(n)\),因此需要 \(Θ(n)\) 的空间。
2) 一次遍历
遍历过程:
-
从根节点开始遍历;
-
如果当前节点的值大于 p 和 q 的值,说明 p 和 q 应该在当前节点的左子树,因此将当前节点移动到它的左子节点;
-
如果当前节点的值小于 p 和 q 的值,说明 p 和 q 应该在当前节点的右子树,因此将当前节点移动到它的右子节点;
-
如果当前节点的值不满足上述两条要求,那么说明当前节点就是「分岔点」。此时,p 和 q 要么在当前节点的不同的子树中,要么其中一个就是当前节点。
可以发现,如果将这两个节点放在一起遍历,就省去了存储路径需要的空间。
Java-代码🌳
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
TreeNode ancestor = root;
while (true) {
if (p.val < ancestor.val && q.val < ancestor.val) {
ancestor = ancestor.left;
} else if (p.val > ancestor.val && q.val > ancestor.val) {
ancestor = ancestor.right;
} else {
break;
}
}
return ancestor;
}
}
C++-代码🌳
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
TreeNode* ancestor = root;
while (true) {
if (p->val < ancestor->val && q->val < ancestor->val) {
ancestor = ancestor->left;
}
else if (p->val > ancestor->val && q->val > ancestor->val) {
ancestor = ancestor->right;
}
else {
break;
}
}
return ancestor;
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 \(n\) 是给定的二叉搜索树中的节点个数。
-
空间复杂度:\(O(1)\)。
449. 序列化和反序列化二叉搜索树
序列化是将数据结构或对象转换为一系列位的过程,以便它可以存储在文件或内存缓冲区中,或通过网络连接链路传输,以便稍后在同一个或另一个计算机环境中重建。
设计一个算法来序列化和反序列化二叉搜索树。 对序列化/反序列化算法的工作方式没有限制。只需确保二叉搜索树可以序列化为字符串,并且可以将该字符串反序列化为最初的二叉搜索树。
编码的字符串应尽可能紧凑。题目数据保证输入的树是一棵二叉搜索树。
示例 1:
输入:root = [2,1,3]
输出:[2,1,3]
示例 2:
输入:root = []
输出:[]
后序遍历
给定一棵二叉树的「先序遍历」和「中序遍历」可以恢复这颗二叉树。给定一棵二叉树的「后序遍历」和「中序遍历」也可以恢复这颗二叉树。而对于二叉搜索树,给定「先序遍历」或者「后序遍历」,对其经过排序即可得到「中序遍历」。因此,仅对二叉搜索树做「先序遍历」或者「后序遍历」,即可达到序列化和反序列化的要求。此题解采用「后序遍历」的方法。
序列化时,只需要对二叉搜索树进行后序遍历,再将数组编码成字符串即可。
反序列化时,需要先将字符串解码成后序遍历的数组。在将后序遍历的数组恢复成二叉搜索树时,不需要先排序得到中序遍历的数组再根据中序和后序遍历的数组来恢复二叉树,而可以根据有序性直接由后序遍历的数组恢复二叉搜索树。后序遍历得到的数组中,根结点的值位于数组末尾,左子树的节点均小于根节点的值,右子树的节点均大于根节点的值,可以根据这些性质设计递归函数恢复二叉搜索树。
Java-代码🌳
public class Codec {
public String serialize(TreeNode root) {
List<Integer> list = new ArrayList<Integer>();
postOrder(root, list);
String str = list.toString();
return str.substring(1, str.length() - 1);
}
public TreeNode deserialize(String data) {
if (data.isEmpty()) {
return null;
}
String[] arr = data.split(", ");
Deque<Integer> stack = new ArrayDeque<Integer>();
int length = arr.length;
for (int i = 0; i < length; i++) {
stack.push(Integer.parseInt(arr[i]));
}
return construct(Integer.MIN_VALUE, Integer.MAX_VALUE, stack);
}
private void postOrder(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
postOrder(root.left, list);
postOrder(root.right, list);
list.add(root.val);
}
private TreeNode construct(int lower, int upper, Deque<Integer> stack) {
if (stack.isEmpty() || stack.peek() < lower || stack.peek() > upper) {
return null;
}
int val = stack.pop();
TreeNode root = new TreeNode(val);
root.right = construct(val, upper, stack);
root.left = construct(lower, val, stack);
return root;
}
}
C++-代码🌳
class Codec {
public:
string serialize(TreeNode* root) {
string res;
vector<int> arr;
postOrder(root, arr);
if (arr.size() == 0) {
return res;
}
for (int i = 0; i < arr.size() - 1; i++) {
res.append(to_string(arr[i]) + ",");
}
res.append(to_string(arr.back()));
return res;
}
vector<string> split(const string &str, char dec) {
int pos = 0;
int start = 0;
vector<string> res;
while (pos < str.size()) {
while (pos < str.size() && str[pos] == dec) {
pos++;
}
start = pos;
while (pos < str.size() && str[pos] != dec) {
pos++;
}
if (start < str.size()) {
res.emplace_back(str.substr(start, pos - start));
}
}
return res;
}
TreeNode* deserialize(string data) {
if (data.size() == 0) {
return nullptr;
}
vector<string> arr = split(data, ',');
stack<int> st;
for (auto & str : arr) {
st.emplace(stoi(str));
}
return construct(INT_MIN, INT_MAX, st);
}
void postOrder(TreeNode *root,vector<int> & arr) {
if (root == nullptr) {
return;
}
postOrder(root->left, arr);
postOrder(root->right, arr);
arr.emplace_back(root->val);
}
TreeNode * construct(int lower, int upper, stack<int> & st) {
if (st.size() == 0 || st.top() < lower || st.top() > upper) {
return nullptr;
}
int val = st.top();
st.pop();
TreeNode *root = new TreeNode(val);
root->right = construct(val, upper, st);
root->left = construct(lower, val, st);
return root;
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 \(n\) 是树的节点数。serialize 需要 \(O(n)\) 时间遍历每个点。deserialize 需要 \(O(n)\) 时间恢复每个点。
-
空间复杂度:\(O(n)\),其中 \(n\) 是树的节点数。serialize 需要 \(O(n)\) 空间用数组保存每个点的值,递归的深度最深也为 \(O(n)\)。deserialize 需要 \(O(n)\) 空间用数组保存每个点的值,递归的深度最深也为 \(O(n)\)。
450. 删除二叉搜索树中的节点
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。节点值唯一,
root 是合法的二叉搜索树。
一般来说,删除节点可分为两个步骤:
-
首先找到需要删除的节点;
-
如果找到了,删除它。
示例 1:
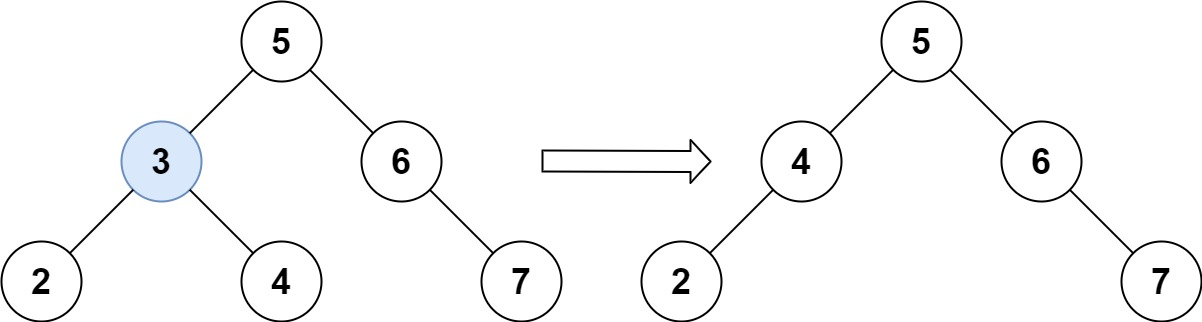
输入:root = [5,3,6,2,4,null,7], key = 3
输出:[5,4,6,2,null,null,7]
解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。
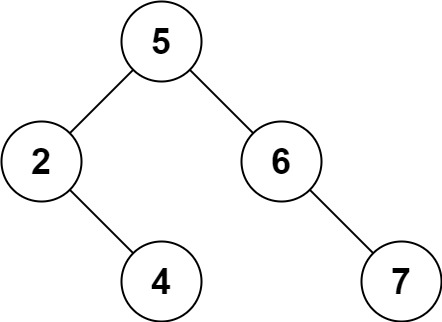
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0
输出: []
1) 递归
分类讨论:
- root 为空,代表未搜索到值为 key 的节点,返回空。
- root.val>key,表示值为 key 的节点可能存在于 root 的左子树中,需要递归地在 root.left 调用 deleteNode,并返回 root。
- root.val<key,表示值为 key 的节点可能存在于 root 的右子树中,需要递归地在 root.right 调用 deleteNode,并返回 root。
- root.val=key,root 即为要删除的节点。此时要做的是删除 root,并将它的子树合并成一棵子树,保持有序性,并返回根节点。根据 root 的子树情况分成以下情况讨论:
- root 为叶子节点,没有子树。此时可以直接将它删除,即返回空。
- root 只有左子树,没有右子树。此时可以将它的左子树作为新的子树,返回它的左子节点。
- root 只有右子树,没有左子树。此时可以将它的右子树作为新的子树,返回它的右子节点。
- root 有左右子树,这时可以将 root 的后继节点(比 root 大的最小节点,即它的右子树中的最小节点,记为 successor)作为新的根节点替代 root,并将 successor 从 root 的右子树中删除,使得在保持有序性的情况下合并左右子树。
- 简单证明,successor 位于 root 的右子树中,因此大于 root 的所有左子节点;successor 是 root 的右子树中的最小节点,因此小于 root 的右子树中的其他节点。以上两点保持了新子树的有序性。
- 实现:可以先寻找 successor,再删除它。successor 是 root 的右子树中的最小节点,可以先找到 root 的右子节点,再不停地往左子节点寻找,直到找到一个不存在左子节点的节点,这个节点即为 successor。然后递归地在 root.right 调用 deleteNode 来删除 successor。因为 successor 没有左子节点,因此这一步递归调用不会再次步入这一种情况。然后将 successor 更新为新的 root 并返回。
Java-代码🌳
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null) {
return null;
}
if (root.val > key) {
root.left = deleteNode(root.left, key);
return root;
}
if (root.val < key) {
root.right = deleteNode(root.right, key);
return root;
}
if (root.val == key) {
if (root.left == null && root.right == null) {
return null;
}
if (root.right == null) {
return root.left;
}
if (root.left == null) {
return root.right;
}
TreeNode successor = root.right;
while (successor.left != null) {
successor = successor.left;
}
root.right = deleteNode(root.right, successor.val); //!
successor.right = root.right;
successor.left = root.left;
return successor;
}
return root;
}
}
C++-代码🌳
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if (root == nullptr) {
return nullptr;
}
if (root->val > key) {
root->left = deleteNode(root->left, key);
return root;
}
if (root->val < key) {
root->right = deleteNode(root->right, key);
return root;
}
if (root->val == key) {
if (!root->left && !root->right) {
return nullptr;
}
if (!root->right) {
return root->left;
}
if (!root->left) {
return root->right;
}
TreeNode *successor = root->right;
while (successor->left) {
successor = successor->left;
}
root->right = deleteNode(root->right, successor->val);
successor->right = root->right;
successor->left = root->left;
return successor;
}
return root;
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 \(n\) 为 root 的节点个数。最差情况下,寻找和删除 successor 各需要遍历一次树。
-
空间复杂度:\(O(n)\),其中 \(n\) 为 root 的节点个数。递归的深度最深为 \(O(n)\)。
2) 迭代
寻找并删除 successor 时,也可以用一个变量保存它的父节点,从而可以节省一步递归操作。
Java-代码🌳
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
TreeNode cur = root, curParent = null;
while (cur != null && cur.val != key) {
curParent = cur;
if (cur.val > key) {
cur = cur.left;
} else {
cur = cur.right;
}
}
if (cur == null) {
return root;
}
if (cur.left == null && cur.right == null) {
cur = null;
} else if (cur.right == null) {
cur = cur.left;
} else if (cur.left == null) {
cur = cur.right;
} else {
TreeNode successor = cur.right, successorParent = cur;
while (successor.left != null) {
successorParent = successor;
successor = successor.left;
}
if (successorParent.val == cur.val) {
successorParent.right = successor.right;
} else {
successorParent.left = successor.right;
}
successor.right = cur.right;
successor.left = cur.left;
cur = successor;
}
if (curParent == null) {
return cur;
} else {
if (curParent.left != null && curParent.left.val == key) {
curParent.left = cur;
} else {
curParent.right = cur;
}
return root;
}
}
}
C++-代码🌳
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
TreeNode *cur = root, *curParent = nullptr;
while (cur && cur->val != key) {
curParent = cur;
if (cur->val > key) {
cur = cur->left;
} else {
cur = cur->right;
}
}
if (!cur) {
return root;
}
if (!cur->left && !cur->right) {
cur = nullptr;
} else if (!cur->right) {
cur = cur->left;
} else if (!cur->left) {
cur = cur->right;
} else {
TreeNode *successor = cur->right, *successorParent = cur;
while (successor->left) {
successorParent = successor;
successor = successor->left;
}
if (successorParent->val == cur->val) {
successorParent->right = successor->right;
} else {
successorParent->left = successor->right;
}
successor->right = cur->right;
successor->left = cur->left;
cur = successor;
}
if (!curParent) {
return cur;
} else {
if (curParent->left && curParent->left->val == key) {
curParent->left = cur;
} else {
curParent->right = cur;
}
return root;
}
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 \(n\) 为 root 的节点个数。最差情况下,需要遍历一次树。
-
空间复杂度:\(O(1)\)。使用的空间为常数。
501. 二叉搜索树中的众数
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按任意顺序返回。
假定 BST 满足如下定义:
-
结点左子树中所含节点的值小于等于当前节点的值
-
结点右子树中所含节点的值大于等于当前节点的值
-
左子树和右子树都是二叉搜索树
进阶:你可以不使用额外的空间吗?(假设由递归产生的隐式调用栈的开销不被计算在内)
1) 中序遍历
一个最朴素的做法:对这棵树进行中序遍历,然后从扫描中序遍历序列,然后用一个哈希表来统计每个数字出现的个数,找到出现次数最多的数字。其空间复杂度是 O(n)。
不使用哈希表,一棵二叉搜索树的中序遍历序列是一个非递减的有序序列,因此中序遍历序列中重复出现的数字一定是一个连续出现的,如 {−1,0,0,1,2,2} 中的 0 和 2,所有的 0 都集中在一个连续的段内,所有的 2 也集中在一个连续的段内。可以顺序扫描中序遍历序列,用 base 记录当前的数字,用 count 记录当前数字重复的次数,用 maxCount 来维护已经扫描过的数当中出现最多的那个数字的出现次数,用 answer 数组记录出现的众数。每次扫描到一个新的元素:
-
首先更新 base 和 count:
- 如果该元素和 base 相等,那么 count 自增 1;
- 否则将 base 更新为当前数字,count 复位为 1。
-
然后更新maxCount:
- 如果 count=maxCount,那么说明当前的这个数字(base)出现的次数等于当前众数出现的次数,将 base 加入 answer 数组;
- 如果 count>maxCount,那么说明当前的这个数字(base)出现的次数大于当前众数出现的次数,因此,需要将 maxCount 更新为 count,清空 answer 数组后将 base 加入 answer 数组。
可以把这个过程写成一个 update 函数。这样在寻找出现次数最多的数字的时候就可以省去一个哈希表带来的空间消耗。
然后,考虑不存储这个中序遍历序列。 如果在递归进行中序遍历的过程中,访问当了某个点的时候直接使用上面的 update 函数,就可以省去中序遍历序列的空间,代码如下。
Java-代码🌳
class Solution {
List<Integer> answer = new ArrayList<Integer>();
int base, count, maxCount;
public int[] findMode(TreeNode root) {
dfs(root);
int[] mode = new int[answer.size()];
for (int i = 0; i < answer.size(); ++i) {
mode[i] = answer.get(i);
}
return mode;
}
public void dfs(TreeNode o) {
if (o == null) {
return;
}
dfs(o.left);
update(o.val);
dfs(o.right);
}
public void update(int x) {
if (x == base) {
++count;
} else {
count = 1;
base = x;
}
if (count == maxCount) {
answer.add(base);
}
if (count > maxCount) {
maxCount = count;
answer.clear();
answer.add(base);
}
}
}
C++-代码🌳
class Solution {
public:
vector<int> answer;
int base, count, maxCount;
void update(int x) {
if (x == base) {
++count;
} else {
count = 1;
base = x;
}
if (count == maxCount) {
answer.push_back(base);
}
if (count > maxCount) {
maxCount = count;
answer = vector<int> {base};
}
}
void dfs(TreeNode* o) {
if (!o) {
return;
}
dfs(o->left);
update(o->val);
dfs(o->right);
}
vector<int> findMode(TreeNode* root) {
dfs(root);
return answer;
}
};
复杂度分析
-
时间复杂度:\(O(n)\)。即遍历这棵树的复杂度。
-
空间复杂度:\(O(n)\)。即递归的栈空间的空间代价。
2) Morris 中序遍历
Morris 中序遍历的一个重要步骤就是寻找当前节点的前驱节点,并且 Morris 中序遍历寻找下一个点始终是通过转移到 right 指针指向的位置来完成的。
-
如果当前节点没有左子树,则遍历这个点,然后跳转到当前节点的右子树。
-
如果当前节点有左子树,那么它的前驱节点一定在左子树上,可以在左子树上一直向右行走,找到当前点的前驱节点。
-
如果前驱节点没有右子树,就将前驱节点的 right 指针指向当前节点。这一步是为了在遍历完前驱节点后能找到前驱节点的后继,也就是当前节点。
-
如果前驱节点的右子树为当前节点,说明前驱节点已经被遍历过并被修改了 right 指针,这个时候重新将前驱的右孩子设置为空,遍历当前的点,然后跳转到当前节点的右子树。
-
模板如下:
TreeNode *cur = root, *pre = nullptr;
while (cur) {
if (!cur->left) {
// ...遍历 cur
cur = cur->right;
continue;
}
pre = cur->left;
while (pre->right && pre->right != cur) {
pre = pre->right;
}
if (!pre->right) {
pre->right = cur;
cur = cur->left;
} else {
pre->right = nullptr;
// ...遍历 cur
cur = cur->right;
}
}
Java-代码🌳
class Solution {
int base, count, maxCount;
List<Integer> answer = new ArrayList<Integer>();
public int[] findMode(TreeNode root) {
TreeNode cur = root, pre = null;
while (cur != null) {
if (cur.left == null) {
update(cur.val);
cur = cur.right;
continue;
}
pre = cur.left;
while (pre.right != null && pre.right != cur) {
pre = pre.right;
}
if (pre.right == null) {
pre.right = cur;
cur = cur.left;
} else {
pre.right = null;
update(cur.val);
cur = cur.right;
}
}
int[] mode = new int[answer.size()];
for (int i = 0; i < answer.size(); ++i) {
mode[i] = answer.get(i);
}
return mode;
}
public void update(int x) {
if (x == base) {
++count;
} else {
count = 1;
base = x;
}
if (count == maxCount) {
answer.add(base);
}
if (count > maxCount) {
maxCount = count;
answer.clear();
answer.add(base);
}
}
}
C++-代码🌳
class Solution {
public:
int base, count, maxCount;
vector<int> answer;
void update(int x) {
if (x == base) {
++count;
} else {
count = 1;
base = x;
}
if (count == maxCount) {
answer.push_back(base);
}
if (count > maxCount) {
maxCount = count;
answer = vector<int> {base};
}
}
vector<int> findMode(TreeNode* root) {
TreeNode *cur = root, *pre = nullptr;
while (cur) {
if (!cur->left) {
update(cur->val);
cur = cur->right;
continue;
}
pre = cur->left;
while (pre->right && pre->right != cur) {
pre = pre->right;
}
if (!pre->right) {
pre->right = cur;
cur = cur->left;
} else {
pre->right = nullptr;
update(cur->val);
cur = cur->right;
}
}
return answer;
}
};
复杂度分析
- 时间复杂度:\(O(n)\)。每个点被访问的次数不会超过两次,故这里的时间复杂度是 \(O(n)\)。
- 空间复杂度:\(O(1)\)。使用临时空间的大小和输入规模无关。
530. 二叉搜索树的最小绝对差
给你一个二叉搜索树的根节点 root ,返回树中任意两不同节点值之间的最小差值。
差值是一个正数,其数值等于两值之差的绝对值。
中序遍历
对升序数组 a 求任意两个元素之差的绝对值的最小值,答案一定为相邻两个元素之差的最小值。
在中序遍历的过程中用 pre 变量保存前驱节点的值,边遍历边更新答案,不需要显式创建数组来保存,需要注意的是 pre 的初始值需要设置成任意负数标记开头。
Java-代码🌳
class Solution {
int pre;
int ans;
public int getMinimumDifference(TreeNode root) {
ans = Integer.MAX_VALUE;
pre = -1;
dfs(root);
return ans;
}
public void dfs(TreeNode root) {
if (root == null) {
return;
}
dfs(root.left);
if (pre == -1) {
pre = root.val;
} else {
ans = Math.min(ans, root.val - pre);
pre = root.val;
}
dfs(root.right);
}
}
C++-代码🌳
class Solution {
public:
void dfs(TreeNode* root, int& pre, int& ans) {
if (root == nullptr) {
return;
}
dfs(root->left, pre, ans);
if (pre == -1) {
pre = root->val;
} else {
ans = min(ans, root->val - pre);
pre = root->val;
}
dfs(root->right, pre, ans);
}
int getMinimumDifference(TreeNode* root) {
int ans = INT_MAX, pre = -1;
dfs(root, pre, ans);
return ans;
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 \(n\) 为二叉搜索树节点的个数。每个节点在中序遍历中都会被访问一次且只会被访问一次,因此总时间复杂度为 \(O(n)\)。
-
空间复杂度:\(O(n)\)。递归函数的空间复杂度取决于递归的栈深度,而栈深度在二叉搜索树为一条链的情况下会达到 \(O(n)\) 级别。
538. 把二叉搜索树转换为累加树
给出二叉搜索树的根节点,该树的节点值各不相同,将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
-
节点的左子树仅包含键小于节点键的节点。
-
节点的右子树仅包含键大于节点键的节点。
-
左右子树也必须是二叉搜索树。
注:本题和 1038.从二叉搜索树到更大和树 相同
1) 反序中序遍历
二叉搜索树的中序遍历是一个单调递增的有序序列。如果反序地中序遍历该二叉搜索树,即可得到一个单调递减的有序序列。
将每个节点的值修改为原来的节点值加上所有大于它的节点值之和。这样只需要反序中序遍历该二叉搜索树,记录过程中的节点值之和,并不断更新当前遍历到的节点的节点值,即可得到累加树。
Java-代码🌳
class Solution {
int sum = 0;
public TreeNode convertBST(TreeNode root) {
if (root != null) {
convertBST(root.right);
sum += root.val;
root.val = sum;
convertBST(root.left);
}
return root;
}
}
C++-代码🌳
class Solution {
public:
int sum = 0;
TreeNode* convertBST(TreeNode* root) {
if (root != nullptr) {
convertBST(root->right);
sum += root->val;
root->val = sum;
convertBST(root->left);
}
return root;
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 \(n\) 是二叉搜索树的节点数。每一个节点恰好被遍历一次。
-
空间复杂度:\(O(n)\),为递归过程中栈的开销,平均情况下为 \(O(logn)\),最坏情况下树呈现链状,为 \(O(n)\)。
2) Morris 遍历
只占用常数空间来实现中序遍历。
Morris 遍历的核心思想是利用树的大量空闲指针,实现空间开销的极限缩减。其反序中序遍历规则总结如下:
-
如果当前节点的右子节点为空,处理当前节点,并遍历当前节点的左子节点;
-
如果当前节点的右子节点不为空,找到当前节点右子树的最左节点(该节点为当前节点中序遍历的前驱节点);
-
如果最左节点的左指针为空,将最左节点的左指针指向当前节点,遍历当前节点的右子节点;
-
如果最左节点的左指针不为空,将最左节点的左指针重新置为空(恢复树的原状),处理当前节点,并将当前节点置为其左节点;
-
-
重复步骤 1 和步骤 2,直到遍历结束。
这样利用 Morris 遍历的方法,反序中序遍历该二叉搜索树,即可实现线性时间与常数空间的遍历。
Java-代码🌳
class Solution {
public TreeNode convertBST(TreeNode root) {
int sum = 0;
TreeNode node = root;
while (node != null) {
if (node.right == null) {
sum += node.val;
node.val = sum;
node = node.left;
} else {
TreeNode succ = getSuccessor(node);
if (succ.left == null) {
succ.left = node;
node = node.right;
} else {
succ.left = null;
sum += node.val;
node.val = sum;
node = node.left;
}
}
}
return root;
}
public TreeNode getSuccessor(TreeNode node) {
TreeNode succ = node.right;
while (succ.left != null && succ.left != node) {
succ = succ.left;
}
return succ;
}
}
C++-代码🌳
class Solution {
public:
TreeNode* getSuccessor(TreeNode* node) {
TreeNode* succ = node->right;
while (succ->left != nullptr && succ->left != node) {
succ = succ->left;
}
return succ;
}
TreeNode* convertBST(TreeNode* root) {
int sum = 0;
TreeNode* node = root;
while (node != nullptr) {
if (node->right == nullptr) {
sum += node->val;
node->val = sum;
node = node->left;
} else {
TreeNode* succ = getSuccessor(node);
if (succ->left == nullptr) {
succ->left = node;
node = node->right;
} else {
succ->left = nullptr;
sum += node->val;
node->val = sum;
node = node->left;
}
}
}
return root;
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 \(n\) 是二叉搜索树的节点数。没有左子树的节点只被访问一次,有左子树的节点被访问两次。
-
空间复杂度:\(O(1)\)。只操作已经存在的指针(树的空闲指针),因此只需要常数的额外空间。
653. 两数之和 IV - 输入二叉搜索树
给定一个二叉搜索树 root 和一个目标结果 k,如果二叉搜索树中存在两个元素且它们的和等于给定的目标结果,则返回 true。
深度优先搜索 + 哈希表
可以使用深度优先搜索的方式遍历整棵树,用哈希表记录遍历过的节点的值。
对于一个值为 x 的节点,检查哈希表中是否存在 k−x 即可。如果存在对应的元素,那么就可以在该树上找到两个节点的和为 k;否则,将 x 放入到哈希表中。
如果遍历完整棵树都不存在对应的元素,那么该树上不存在两个和为 k 的节点。
也可以使用广度优先搜索 + 哈希表、深度优先搜索 + 中序遍历 + 双指针等方法。
Java-代码🌳
class Solution {
Set<Integer> set = new HashSet<Integer>();
public boolean findTarget(TreeNode root, int k) {
if (root == null) {
return false;
}
if (set.contains(k - root.val)) {
return true;
}
set.add(root.val);
return findTarget(root.left, k) || findTarget(root.right, k);
}
}
C++-代码🌳
class Solution {
public:
unordered_set<int> hashTable;
bool findTarget(TreeNode *root, int k) {
if (root == nullptr) {
return false;
}
if (hashTable.count(k - root->val)) {
return true;
}
hashTable.insert(root->val);
return findTarget(root->left, k) || findTarget(root->right, k);
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 \(n\) 为二叉搜索树的大小。需要遍历整棵树一次。
-
空间复杂度:\(O(n)\),其中 \(n\) 为二叉搜索树的大小。主要为哈希表的开销,最坏情况下需要将每个节点加入哈希表一次。
669. 修剪二叉搜索树
给你二叉搜索树的根节点 root,同时给定最小边界 low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树不应该改变保留在树中的元素的相对结构 (即,如果没有被移除,原有的父代子代关系都应当保留)。可以证明,存在唯一的答案 。
所以结果应当返回修剪好的二叉搜索树的新的根节点。注意,根节点可能会根据给定的边界发生改变。
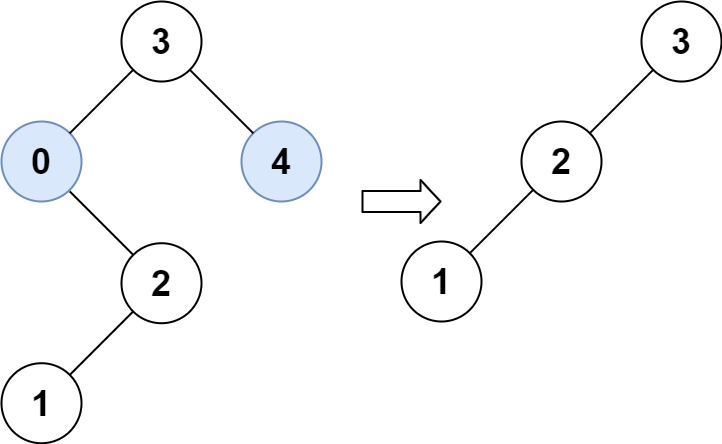
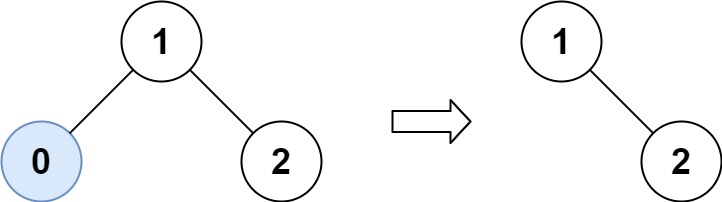
1) 递归
对根结点 root 进行深度优先遍历。
- 对于当前访问的结点,如果结点为空结点,直接返回空结点;
- 如果结点的值小于 low,那么说明该结点及它的左子树都不符合要求,返回对它的右结点进行修剪后的结果;
- 如果结点的值大于 high,那么说明该结点及它的右子树都不符合要求,返回对它的左子树进行修剪后的结果;
- 如果结点的值位于区间 [low,high],将结点的左结点设为对它的左子树修剪后的结果,右结点设为对它的右子树进行修剪后的结果。
Java-代码🌳
class Solution {
public TreeNode trimBST(TreeNode root, int low, int high) {
if (root == null) {
return null;
}
if (root.val < low) {
return trimBST(root.right, low, high);
} else if (root.val > high) {
return trimBST(root.left, low, high);
} else {
root.left = trimBST(root.left, low, high);
root.right = trimBST(root.right, low, high);
return root;
}
}
}
C++-代码🌳
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if (root == nullptr) {
return nullptr;
}
if (root->val < low) {
return trimBST(root->right, low, high);
} else if (root->val > high) {
return trimBST(root->left, low, high);
} else {
root->left = trimBST(root->left, low, high);
root->right = trimBST(root->right, low, high);
return root;
}
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 \(n\) 为二叉树的结点数目。
-
空间复杂度:\(O(n)\)。递归栈最坏情况下需要 \(O(n)\) 的空间。
2) 迭代
如果一个结点 node 符合要求,即它的值位于区间 [low,high],那么它的左子树与右子树应该如何修剪?
先讨论左子树的修剪:
-
node 的左结点为空结点:不需要修剪
-
node 的左结点非空:
-
如果它的左结点left 的值小于 low,那么left 以及 left 的左子树都不符合要求,将 node 的左结点设为 left 的右结点,然后再重新对 node 的左子树进行修剪。
-
如果它的左结点 left 的值大于等于 low,又因为 node 的值已经符合要求,所以 left 的右子树一定符合要求。基于此,只需要对 left 的左子树进行修剪。令 node 等于 left ,然后再重新对 node 的左子树进行修剪。
-
以上过程可以迭代处理。对于右子树的修剪同理。
对根结点进行判断,如果根结点不符合要求,将根结点设为对应的左结点或右结点,直到根结点符合要求,然后将根结点作为符合要求的结点,依次修剪它的左子树与右子树。
Java-代码🌳
class Solution {
public TreeNode trimBST(TreeNode root, int low, int high) {
while (root != null && (root.val < low || root.val > high)) {
if (root.val < low) {
root = root.right;
} else {
root = root.left;
}
}
if (root == null) {
return null;
}
for (TreeNode node = root; node.left != null; ) {
if (node.left.val < low) {
node.left = node.left.right;
} else {
node = node.left;
}
}
for (TreeNode node = root; node.right != null; ) {
if (node.right.val > high) {
node.right = node.right.left;
} else {
node = node.right;
}
}
return root;
}
}
C++-代码🌳
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
while (root && (root->val < low || root->val > high)) {
if (root->val < low) {
root = root->right;
} else {
root = root->left;
}
}
if (root == nullptr) {
return nullptr;
}
for (auto node = root; node->left; ) {
if (node->left->val < low) {
node->left = node->left->right;
} else {
node = node->left;
}
}
for (auto node = root; node->right; ) {
if (node->right->val > high) {
node->right = node->right->left;
} else {
node = node->right;
}
}
return root;
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 \(n\) 为二叉树的结点数目。最多访问 \(n\) 个结点。
-
空间复杂度:\(O(1)\)。
700. 二叉搜索树中的搜索
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
1) 递归
算法:
-
若 root 为空则返回空节点;
-
若 val=root.val,则返回 root;
-
若 val<root.val,递归左子树;
-
若 val>root.val,递归右子树。
Java-代码🌳
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
if (root == null) {
return null;
}
if (val == root.val) {
return root;
}
return searchBST(val < root.val ? root.left : root.right, val);
}
}
C++-代码🌳
class Solution {
public:
TreeNode *searchBST(TreeNode *root, int val) {
if (root == nullptr) {
return nullptr;
}
if (val == root->val) {
return root;
}
return searchBST(val < root->val ? root->left : root->right, val);
}
};
复杂度分析
-
时间复杂度:\(O(N)\),其中 \(N\) 是二叉搜索树的节点数。最坏情况下二叉搜索树是一条链,且要找的元素比链末尾的元素值还要小(大),这种情况下需要递归 \(N\) 次。
-
空间复杂度:\(O(N)\)。最坏情况下递归需要 \(O(N)\) 的栈空间。
2) 迭代
迭代写法:
-
若 root 为空则跳出循环,并返回空节点;
-
若val=root.val,则返回 root;
-
若 val<root.val,将 root 置为 root.left;
-
若 val>root.val,将 root 置为 root.right。
Java-代码🌳
class Solution {
public TreeNode searchBST(TreeNode root, int val) {
while (root != null) {
if (val == root.val) {
return root;
}
root = val < root.val ? root.left : root.right;
}
return null;
}
}
C++-代码🌳
class Solution {
public:
TreeNode *searchBST(TreeNode *root, int val) {
while (root) {
if (val == root->val) {
return root;
}
root = val < root->val ? root->left : root->right;
}
return nullptr;
}
};
复杂度分析
-
时间复杂度:\(O(N)\),其中 \(N\) 是二叉搜索树的节点数。最坏情况下二叉搜索树是一条链,且要找的元素比链末尾的元素值还要小(大),这种情况下需要迭代 \(N\) 次。
-
空间复杂度:\(O(1)\)。没有使用额外的空间。
701. 二叉搜索树中的插入操作
给定二叉搜索树(BST)的根节点 root 和要插入树中的值 value,将值插入二叉搜索树。返回插入后二叉搜索树的根节点。 输入数据保证新值和原始二叉搜索树中的任意节点值都不同。所有值 Node.val 是独一无二的且保证 val 在原始 BST 中不存在。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 可以返回任意有效的结果 。
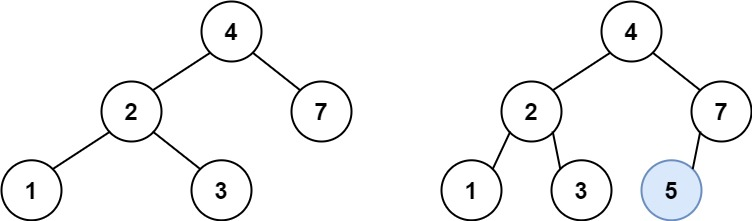
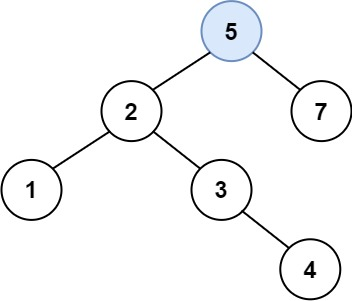
模拟
二叉搜索树的性质:对于任意节点root 而言,左子树(如果存在)上所有节点的值均小于root.val,右子树(如果存在)上所有节点的值均大于 root.val,且它们都是二叉搜索树。
因此,当将 val 插入到以 root 为根的子树上时,根据 val 与 root.val 的大小关系,就可以确定要将 val 插入到哪个子树中。
-
如果该子树不为空,则问题转化成了将 val 插入到对应子树上。
-
否则,在此处新建一个以 val 为值的节点,并链接到其父节点 root 上。
Java-代码🌳
class Solution {
public TreeNode insertIntoBST(TreeNode root, int val) {
if (root == null) {
return new TreeNode(val);
}
TreeNode pos = root;
while (pos != null) {
if (val < pos.val) {
if (pos.left == null) {
pos.left = new TreeNode(val);
break;
} else {
pos = pos.left;
}
} else {
if (pos.right == null) {
pos.right = new TreeNode(val);
break;
} else {
pos = pos.right;
}
}
}
return root;
}
}
C++-代码🌳
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if (root == nullptr) {
return new TreeNode(val);
}
TreeNode* pos = root;
while (pos != nullptr) {
if (val < pos->val) {
if (pos->left == nullptr) {
pos->left = new TreeNode(val);
break;
} else {
pos = pos->left;
}
} else {
if (pos->right == nullptr) {
pos->right = new TreeNode(val);
break;
} else {
pos = pos->right;
}
}
}
return root;
}
};
复杂度分析
-
时间复杂度:\(O(N)\),其中 \(N\) 为树中节点的数目。最坏情况下,需要将值插入到树的最深的叶子结点上,而叶子节点最深为 \(O(N)\)。
-
空间复杂度:\(O(1)\)。只使用了常数大小的空间。
897. 递增顺序搜索树
给你一棵二叉搜索树的 root ,请你按中序遍历将其重新排列为一棵递增顺序搜索树,使树中最左边的节点成为树的根节点,并且每个节点没有左子节点,只有一个右子节点。
示例 1:
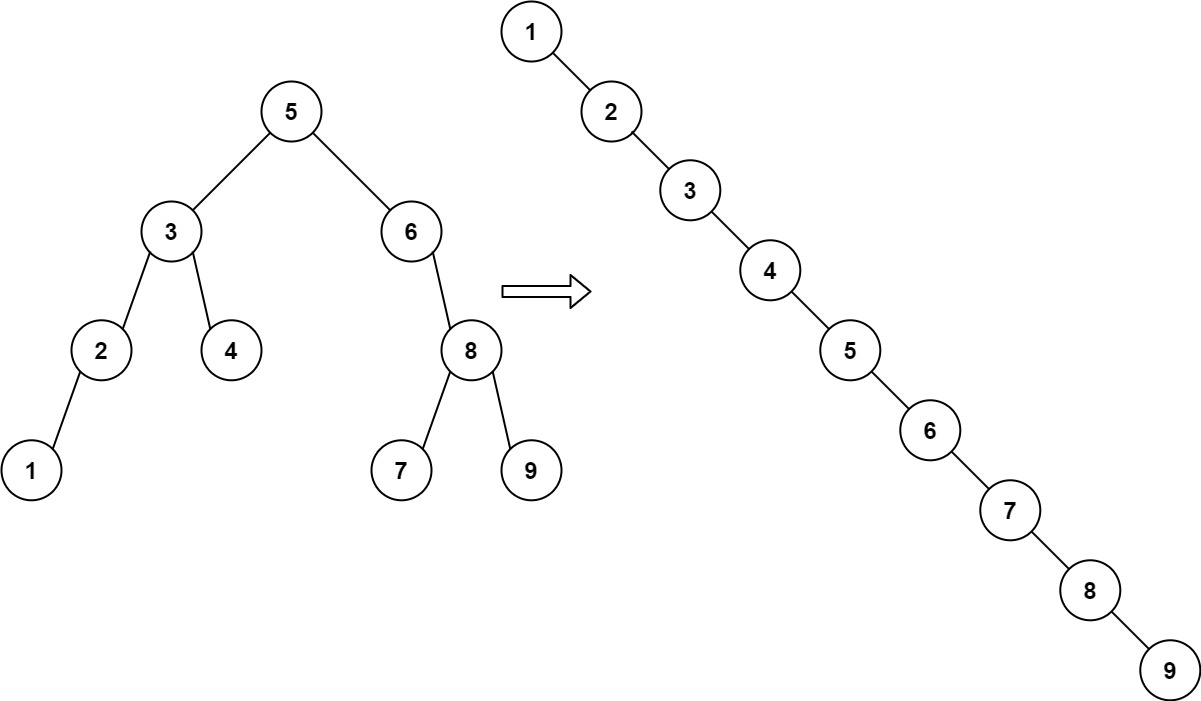
1) 中序遍历之后生成新的树
-
先对输入的二叉搜索树执行中序遍历,将结果保存到一个列表中;
-
然后根据列表中的节点值,创建等价的只含有右节点的二叉搜索树,其过程等价于根据节点值创建一个链表。
Java-代码🌳
class Solution {
public TreeNode increasingBST(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
inorder(root, res);
TreeNode dummyNode = new TreeNode(-1);
TreeNode currNode = dummyNode;
for (int value : res) {
currNode.right = new TreeNode(value);
currNode = currNode.right;
}
return dummyNode.right;
}
public void inorder(TreeNode node, List<Integer> res) {
if (node == null) {
return;
}
inorder(node.left, res);
res.add(node.val);
inorder(node.right, res);
}
}
C++-代码🌳
class Solution {
public:
void inorder(TreeNode *node, vector<int> &res) {
if (node == nullptr) {
return;
}
inorder(node->left, res);
res.push_back(node->val);
inorder(node->right, res);
}
TreeNode *increasingBST(TreeNode *root) {
vector<int> res;
inorder(root, res);
TreeNode *dummyNode = new TreeNode(-1);
TreeNode *currNode = dummyNode;
for (int value : res) {
currNode->right = new TreeNode(value);
currNode = currNode->right;
}
return dummyNode->right;
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 \(n\) 是二叉搜索树的节点总数。
-
空间复杂度:\(O(n)\),其中 \(n\) 是二叉搜索树的节点总数。需要长度为 \(n\) 的列表保存二叉搜索树的所有节点的值。
2) 在中序遍历的过程中改变节点指向🍓
当遍历到一个节点时,把它的左孩子设为空,并将其本身作为上一个遍历到的节点的右孩子。递归遍历的过程中,由于递归函数的调用栈保存了节点的引用,因此上述操作可以实现。
Java-代码🌳
class Solution {
private TreeNode resNode;
public TreeNode increasingBST(TreeNode root) {
TreeNode dummyNode = new TreeNode(-1);
resNode = dummyNode;
inorder(root);
return dummyNode.right;
}
public void inorder(TreeNode node) {
if (node == null) {
return;
}
inorder(node.left);
// 在中序遍历的过程中修改节点指向
resNode.right = node;
node.left = null;
resNode = node;
inorder(node.right);
}
}
C++-代码🌳
class Solution {
private:
TreeNode *resNode;
public:
void inorder(TreeNode *node) {
if (node == nullptr) {
return;
}
inorder(node->left);
// 在中序遍历的过程中修改节点指向
resNode->right = node;
node->left = nullptr;
resNode = node;
inorder(node->right);
}
TreeNode *increasingBST(TreeNode *root) {
TreeNode *dummyNode = new TreeNode(-1);
resNode = dummyNode;
inorder(root);
return dummyNode->right;
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 \(n\) 是二叉搜索树的节点总数。
-
空间复杂度:\(O(n)\)。递归过程中的栈空间开销为 \(O(n)\)。
938. 二叉搜索树的范围和
给定二叉搜索树的根结点 root,返回值位于范围 [low, high] 之间的所有结点的值的和,所有 Node.val 互不相同。
1) 深度优先搜索
按深度优先搜索的顺序计算范围和。记当前子树根节点为 root,分以下四种情况讨论:
-
root 节点为空
返回 0。
-
root 节点的值大于 high
由于二叉搜索树右子树上所有节点的值均大于根节点的值,即均大于 high,故无需考虑右子树,返回左子树的范围和。
-
root 节点的值小于 low
由于二叉搜索树左子树上所有节点的值均小于根节点的值,即均小于 low,故无需考虑左子树,返回右子树的范围和。
-
root 节点的值在 [low,high] 范围内
此时应返回 root 节点的值、左子树的范围和、右子树的范围和这三者之和。
Java-代码🌳
class Solution {
public int rangeSumBST(TreeNode root, int low, int high) {
if (root == null) {
return 0;
}
if (root.val > high) {
return rangeSumBST(root.left, low, high);
}
if (root.val < low) {
return rangeSumBST(root.right, low, high);
}
return root.val + rangeSumBST(root.left, low, high) + rangeSumBST(root.right, low, high);
}
}
C++-代码🌳
class Solution {
public:
int rangeSumBST(TreeNode *root, int low, int high) {
if (root == nullptr) {
return 0;
}
if (root->val > high) {
return rangeSumBST(root->left, low, high);
}
if (root->val < low) {
return rangeSumBST(root->right, low, high);
}
return root->val + rangeSumBST(root->left, low, high) + rangeSumBST(root->right, low, high);
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 \(n\) 是二叉搜索树的节点数。
-
空间复杂度:\(O(n)\)。空间复杂度主要取决于栈空间的开销。
2) 广度优先搜索
使用广度优先搜索的方法,用一个队列 q 存储需要计算的节点。每次取出队首节点时,若节点为空则跳过该节点,否则按方法一中给出的大小关系来决定加入队列的子节点。
Java-代码🌳
class Solution {
public int rangeSumBST(TreeNode root, int low, int high) {
int sum = 0;
Queue<TreeNode> q = new LinkedList<TreeNode>();
q.offer(root);
while (!q.isEmpty()) {
TreeNode node = q.poll();
if (node == null) {
continue;
}
if (node.val > high) {
q.offer(node.left);
} else if (node.val < low) {
q.offer(node.right);
} else {
sum += node.val;
q.offer(node.left);
q.offer(node.right);
}
}
return sum;
}
}
C++-代码🌳
class Solution {
public:
int rangeSumBST(TreeNode *root, int low, int high) {
int sum = 0;
queue<TreeNode*> q({root});
while (!q.empty()) {
auto node = q.front();
q.pop();
if (node == nullptr) {
continue;
}
if (node->val > high) {
q.push(node->left);
} else if (node->val < low) {
q.push(node->right);
} else {
sum += node->val;
q.push(node->left);
q.push(node->right);
}
}
return sum;
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 \(n\) 是二叉搜索树的节点数。
-
空间复杂度:\(O(n)\)。空间复杂度主要取决于队列的空间。
1008. 前序遍历构造二叉搜索树
给定一个整数数组,它表示BST(即 二叉搜索树 )的先序遍历 ,构造树并返回其根。
保证对于给定的测试用例,总是有可能找到具有给定需求的二叉搜索树。
二叉搜索树是一棵二叉树,其中每个节点,Node.left 的任何后代的值严格小于 Node.val ,Node.right 的任何后代的值严格大于 Node.val。
二叉树的前序遍历首先显示节点的值,然后遍历 Node.left,最后遍历 Node.right。
先序遍历中的值互不相同。
1) 使用先序遍历和中序遍历构造二叉树❌
对「前序遍历」的结果 排序 得到「中序遍历」的结果。
递归实现
Java-代码🌳
public class Solution {
public TreeNode bstFromPreorder(int[] preorder) {
int len = preorder.length;
Map<Integer, Integer> hashMap = new HashMap<>();
int[] inorder = new int[len];
System.arraycopy(preorder, 0, inorder, 0, len);
Arrays.sort(inorder);
int index = 0;
for (Integer value : inorder) {
hashMap.put(value, index);
index++;
}
return dfs(0, len - 1, 0, len - 1, preorder, hashMap);
}
public TreeNode dfs(int preLeft, int preRight, int inLeft, int inRight, int[] preorder, Map<Integer, Integer> hashMap) {
if (preLeft > preRight || inLeft > inRight) {
return null;
}
int pivot = preorder[preLeft];
TreeNode root = new TreeNode(pivot);
int pivotIndex = hashMap.get(pivot);
root.left = dfs(preLeft + 1, pivotIndex - inLeft + preLeft,
inLeft, pivotIndex - 1, preorder, hashMap);
root.right = dfs(pivotIndex - inLeft + preLeft + 1, preRight,
pivotIndex + 1, inRight, preorder, hashMap);
return root;
}
}
C++-代码🌳
class Solution {
private:
unordered_map<int, int> index;
public:
TreeNode* bstFromPreorder(vector<int>& preorder) {
int n = preorder.size();
vector<int> inorder(preorder);
//vector<int> inorder(n);
//inorder.assign(preorder.begin(), preorder.end());
sort(inorder.begin(), inorder.end());
for (int i = 0; i < n; ++i) {
index[inorder[i]] = i;
}
return buildTree(preorder, inorder, 0, n - 1, 0, n - 1);
}
TreeNode* buildTree(const vector<int>& preorder, const vector<int>& inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
if (preorder_left > preorder_right) {
return nullptr;
}
// 前序遍历中的第一个节点就是根节点
int preorder_root = preorder_left;
// 在中序遍历中定位根节点
int inorder_root = index[preorder[preorder_root]];
// 先把根节点建立出来
TreeNode* root = new TreeNode(preorder[preorder_root]);
// 得到左子树中的节点数目
int size_left_subtree = inorder_root - inorder_left;
// 递归地构造左子树,并连接到根节点
// 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
root->left = buildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
// 递归地构造右子树,并连接到根节点
// 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
root->right = buildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
return root;
}
};
复杂度分析
-
时间复杂度:\(O(NlogN)\)。对先序遍历进行排序的时间复杂度为 \(O(NlogN)\),构造二叉搜索树的时间复杂度为 \(O(N)\),因此总的时间复杂度为 \(O(NlogN)\)。
-
空间复杂度:\(O(N)\),中序遍历使用的数组的空间为 \(O(N)\)。
迭代实现
Java-代码🌳
public class Solution {
public TreeNode bstFromPreorder(int[] preorder) {
int len = preorder.length;
if (preorder == null || len == 0) {
return null;
}
int[] inorder = new int[len];
System.arraycopy(preorder, 0, inorder, 0, len);
Arrays.sort(inorder);
TreeNode root = new TreeNode(preorder[0]);
Deque<TreeNode> stack = new LinkedList<TreeNode>();
stack.push(root);
int inorderIndex = 0;
for (int i = 1; i < preorder.length; i++) {
int preorderVal = preorder[i];
TreeNode node = stack.peek();
if (node.val != inorder[inorderIndex]) {
node.left = new TreeNode(preorderVal);
stack.push(node.left);
} else {
while (!stack.isEmpty() && stack.peek().val == inorder[inorderIndex]) {
node = stack.pop();
inorderIndex++;
}
node.right = new TreeNode(preorderVal);
stack.push(node.right);
}
}
return root;
}
}
C++-代码🌳
class Solution {
public:
TreeNode* bstFromPreorder(vector<int>& preorder) {
int n = preorder.size();
if(n==0) return nullptr;
vector<int> inorder(preorder);
//vector<int> inorder(n);
//inorder.assign(preorder.begin(), preorder.end());
sort(inorder.begin(), inorder.end());
TreeNode* root = new TreeNode(preorder[0]);
stack<TreeNode*> stk;
stk.push(root);
int inorderIndex = 0;
for (int i = 1; i < preorder.size(); ++i) {
int preorderVal = preorder[i];
TreeNode* node = stk.top();
if (node->val != inorder[inorderIndex]) {
node->left = new TreeNode(preorderVal);
stk.push(node->left);
}
else {
while (!stk.empty() && stk.top()->val == inorder[inorderIndex]) {
node = stk.top();
stk.pop();
++inorderIndex;
}
node->right = new TreeNode(preorderVal);
stk.push(node->right);
}
}
return root;
}
};
2) 二分查找左右子树的分界线递归构建左右子树
根据「前序遍历」的定义:前序遍历的第 1 个结点一定是二叉树的根结点。
再根据「二叉搜索树」的定义:根据前序遍历的第 1 个结点的值可以把「前序遍历」序列除了第 1 个结点以外后面的部分,分为两个区间:
-
第 1 个子区间里所有的元素都严格小于根结点,可以递归构建成根结点的左子树;
-
第 2 个子区间里所有的元素都严格大于根结点,可以递归构建成根结点的右子树。
使用二分查找找到这两个子区间的分界线。
Java-代码🌳
public class Solution {
public TreeNode bstFromPreorder(int[] preorder) {
int len = preorder.length;
if (len == 0) {
return null;
}
return dfs(preorder, 0, len - 1);
}
private TreeNode dfs(int[] preorder, int left, int right) {
if (left > right) {
return null;
}
TreeNode root = new TreeNode(preorder[left]);
if (left == right) {
return root;
}
// 在区间 [left..right] 里找最后一个小于 preorder[left] 的下标
// 注意这里设置区间的左边界为 left ,不能是 left + 1
// 这是因为考虑到区间只有 2 个元素 [left, right] 的情况,第 1 个部分为空区间,第 2 部分只有一个元素 right
int l = left;
int r = right;
while (l < r) {
int mid = l + (r - l + 1) / 2;
if (preorder[mid] < preorder[left]) {
// 下一轮搜索区间是 [mid, r]
l = mid;
} else {
// 下一轮搜索区间是 [l, mid - 1]
r = mid - 1;
}
}
TreeNode leftTree = dfs(preorder, left + 1, l);
TreeNode rightTree = dfs(preorder, l + 1, right);
root.left = leftTree;
root.right = rightTree;
return root;
}
}
复杂度分析
-
时间复杂度:\(O(NlogN)\),在找左右子树分界线的时候时间复杂度为 \(O(logN)\);
-
空间复杂度:\(O(N)\)。
3) 根据数值上下界递归构建左右子树
使用递归的方法,在扫描先序遍历的同时构造出二叉树。在递归时维护一个 (lower, upper) 二元组,表示当前位置可以插入的节点的值的上下界。如果此时先序遍历位置的值处于上下界中,就将这个值作为新的节点插入到当前位置,并递归地处理当前位置的左右孩子的两个位置。否则回溯到当前位置的父节点。
算法
-
将 lower 和 upper 的初始值分别设置为负无穷和正无穷,因为根节点的值可以为任意值。
-
从先序遍历的第一个元素 idx = 0 开始构造二叉树,构造使用的函数名为 helper(lower, upper):
-
如果 idx = n,即先序遍历中的所有元素已经被添加到二叉树中,那么此时构造已经完成;
-
如果当前 idx 对应的先序遍历中的元素 val = preorder[idx] 的值不在 [lower, upper] 范围内,则进行回溯;
-
如果 idx 对应的先序遍历中的元素 val = preorder[idx] 的值在 [lower, upper] 范围内,则新建一个节点 root,并对其左孩子递归处理 helper(lower, val),对其右孩子递归处理 helper(val, upper)。
-
下图展示了这个过程。
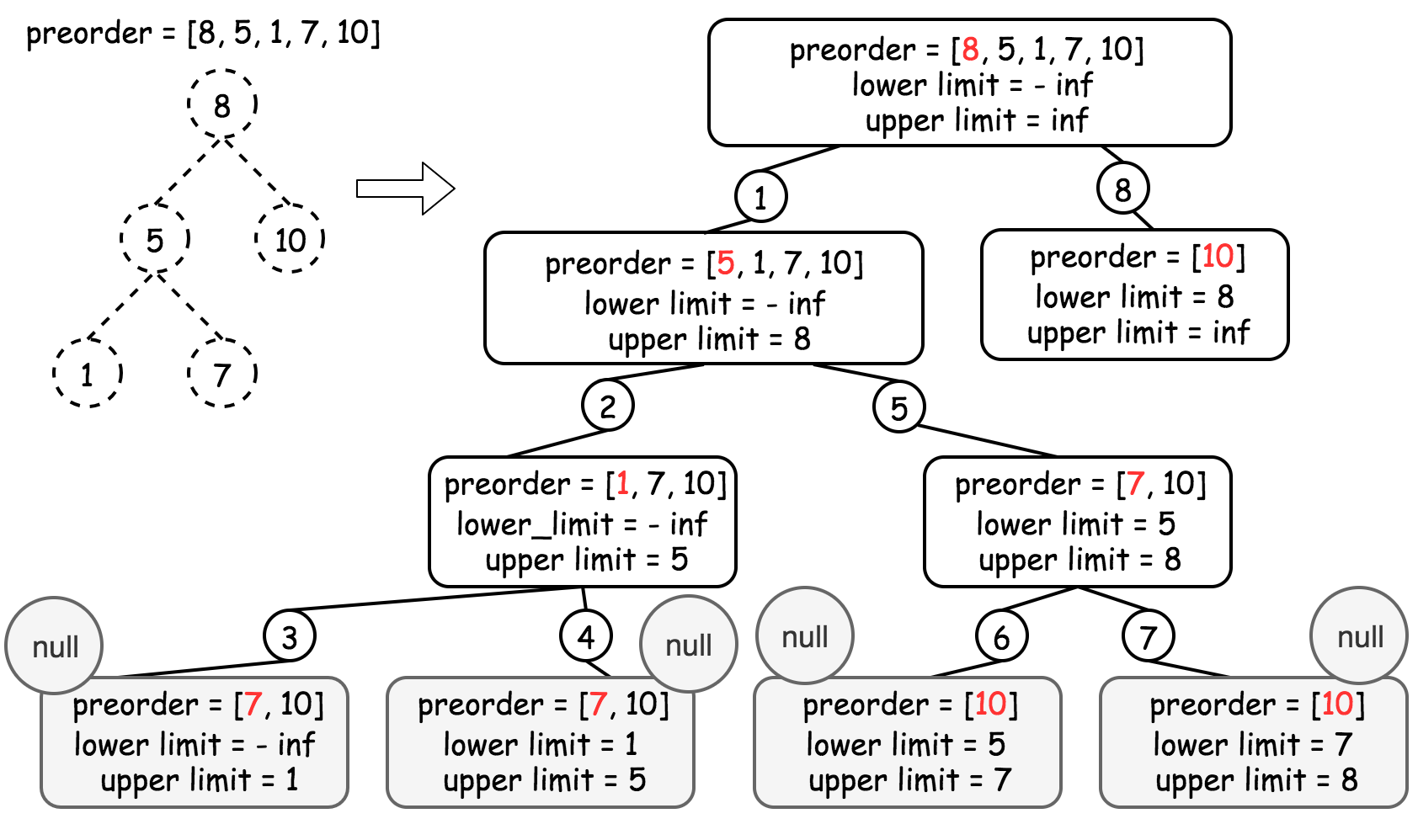
Java-代码🌳
public class Solution {
private int index = 0;
private int[] preorder;
private int len;
//深度优先遍历,遍历的时候把左右边界的值传下去
public TreeNode bstFromPreorder(int[] preorder) {
this.preorder = preorder;
this.len = preorder.length;
return dfs(Integer.MIN_VALUE, Integer.MAX_VALUE);
}
//通过下限和上限来控制指针移动的范围
private TreeNode dfs(int lowerBound, int upperBound) {
// 所有的元素都已经添加到了二叉树中
if (index == len) {
return null;
}
int cur = preorder[index];
if (cur < lowerBound || cur > upperBound) {
return null;
}
index++;
TreeNode root = new TreeNode(cur);
root.left = dfs(lowerBound, cur);
root.right = dfs(cur, upperBound);
return root;
}
}
复杂度分析
-
时间复杂度:\(O(N)\),这里 \(N\) 是输入数组的长度。
-
空间复杂度:\(O(N)\)。
1305. 两棵二叉搜索树中的所有元素
给你 root1 和 root2 这两棵二叉搜索树。请你返回一个列表,其中包含两棵树中的所有整数并按升序排序。.
示例 1:
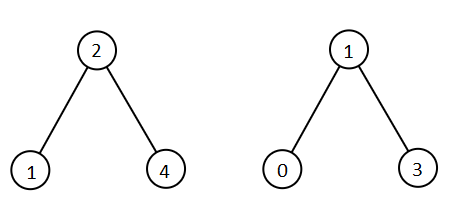
输入:root1 = [2,1,4], root2 = [1,0,3]
输出:[0,1,1,2,3,4]
中序遍历 + 归并
中序遍历这两棵二叉搜索树,可以得到两个有序数组。然后可以使用双指针方法来合并这两个有序数组。
Java-代码🌳
class Solution {
public List<Integer> getAllElements(TreeNode root1, TreeNode root2) {
List<Integer> nums1 = new ArrayList<Integer>();
List<Integer> nums2 = new ArrayList<Integer>();
inorder(root1, nums1);
inorder(root2, nums2);
List<Integer> merged = new ArrayList<Integer>();
int p1 = 0, p2 = 0;
while (true) {
if (p1 == nums1.size()) {
merged.addAll(nums2.subList(p2, nums2.size()));
break;
}
if (p2 == nums2.size()) {
merged.addAll(nums1.subList(p1, nums1.size()));
break;
}
if (nums1.get(p1) < nums2.get(p2)) {
merged.add(nums1.get(p1++));
} else {
merged.add(nums2.get(p2++));
}
}
return merged;
}
public void inorder(TreeNode node, List<Integer> res) {
if (node != null) {
inorder(node.left, res);
res.add(node.val);
inorder(node.right, res);
}
}
}
C++-代码🌳
class Solution {
void inorder(TreeNode *node, vector<int> &res) {
if (node) {
inorder(node->left, res);
res.push_back(node->val);
inorder(node->right, res);
}
}
public:
vector<int> getAllElements(TreeNode *root1, TreeNode *root2) {
vector<int> nums1, nums2;
inorder(root1, nums1);
inorder(root2, nums2);
vector<int> merged;
auto p1 = nums1.begin(), p2 = nums2.begin();
while (true) {
if (p1 == nums1.end()) {
merged.insert(merged.end(), p2, nums2.end());
break;
}
if (p2 == nums2.end()) {
merged.insert(merged.end(), p1, nums1.end());
break;
}
if (*p1 < *p2) {
merged.push_back(*p1++);
} else {
merged.push_back(*p2++);
}
}
return merged;
}
};
复杂度分析
-
时间复杂度:\(O(n+m)\),其中 \(n\) 和 \(m\) 分别为两棵二叉搜索树的节点个数。
-
空间复杂度:\(O(n+m)\)。存储数组以及递归时的栈空间均为 \(O(n+m)\)。
1373. 二叉搜索子树的最大键值和
1) xx
Java-代码🌳
C++-代码🌳
1382. 将二叉搜索树变平衡
给你一棵二叉搜索树,请你返回一棵平衡后的二叉搜索树,新生成的树应该与原来的树有着相同的节点值。如果有多种构造方法,请你返回任意一种。
如果一棵二叉搜索树中,每个节点的两棵子树高度差不超过 1,就称这棵二叉搜索树是平衡的 。

贪心构造
「平衡」要求它是一棵空树或它的左右两个子树的高度差的绝对值不超过 1,左右子树的大小越「平均」,这棵树越平衡。可以通过中序遍历将原来的二叉搜索树转化为一个有序序列,然后对这个有序序列递归建树,对于区间 \([L,R]\):
-
取 \({\rm mid} = \lfloor \frac{L + R}{2} \rfloor\),即中心位置作为当前节点的值;
-
如果 \(L≤mid−1\),那么递归地将区间 \([L,mid−1]\) 作为当前节点的左子树;
-
如果 \(mid+1≤R\),那么递归地将区间 \([mid+1,R]\) 作为当前节点的右子树。
Java-代码🌳
class Solution {
List<Integer> inorderSeq = new ArrayList<Integer>();
public TreeNode balanceBST(TreeNode root) {
getInorder(root);
return build(0, inorderSeq.size() - 1);
}
public void getInorder(TreeNode o) {
if (o.left != null) {
getInorder(o.left);
}
inorderSeq.add(o.val);
if (o.right != null) {
getInorder(o.right);
}
}
public TreeNode build(int l, int r) {
int mid = (l + r) >> 1;
TreeNode o = new TreeNode(inorderSeq.get(mid));
if (l <= mid - 1) {
o.left = build(l, mid - 1);
}
if (mid + 1 <= r) {
o.right = build(mid + 1, r);
}
return o;
}
}
C++-代码🌳
class Solution {
public:
vector<int> inorderSeq;
void getInorder(TreeNode* o) {
if (o->left) {
getInorder(o->left);
}
inorderSeq.push_back(o->val);
if (o->right) {
getInorder(o->right);
}
}
TreeNode* build(int l, int r) {
int mid = (l + r) >> 1;
TreeNode* o = new TreeNode(inorderSeq[mid]);
if (l <= mid - 1) {
o->left = build(l, mid - 1);
}
if (mid + 1 <= r) {
o->right = build(mid + 1, r);
}
return o;
}
TreeNode* balanceBST(TreeNode* root) {
getInorder(root);
return build(0, inorderSeq.size() - 1);
}
};
复杂度分析
假设节点总数为 n。
-
时间复杂度:获得中序遍历的时间代价是 \(O(n)\);建立平衡二叉树的时建立每个点的时间代价为 \(O(1)\),总时间也是 \(O(n)\)。故渐进时间复杂度为 \(O(n)\)。
-
空间复杂度:这里使用了一个数组作为辅助空间,存放中序遍历后的有序序列,故渐进空间复杂度为 \(O(n)\)。
1569. 将子数组重新排序得到同一个二叉搜索树的方案数
1) xx
Java-代码🌳
C++-代码🌳
LCP 52. 二叉搜索树染色
1) xx
Java-代码🌳
C++-代码🌳
剑指 Offer 33. 二叉搜索树的后序遍历序列
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
后序遍历定义: [ 左子树 | 右子树 | 根节点 ] ,即遍历顺序为 “左、右、根” 。
二叉搜索树定义: 左子树中所有节点的值 < 根节点的值;右子树中所有节点的值 > 根节点的值;其左、右子树也分别为二叉搜索树。
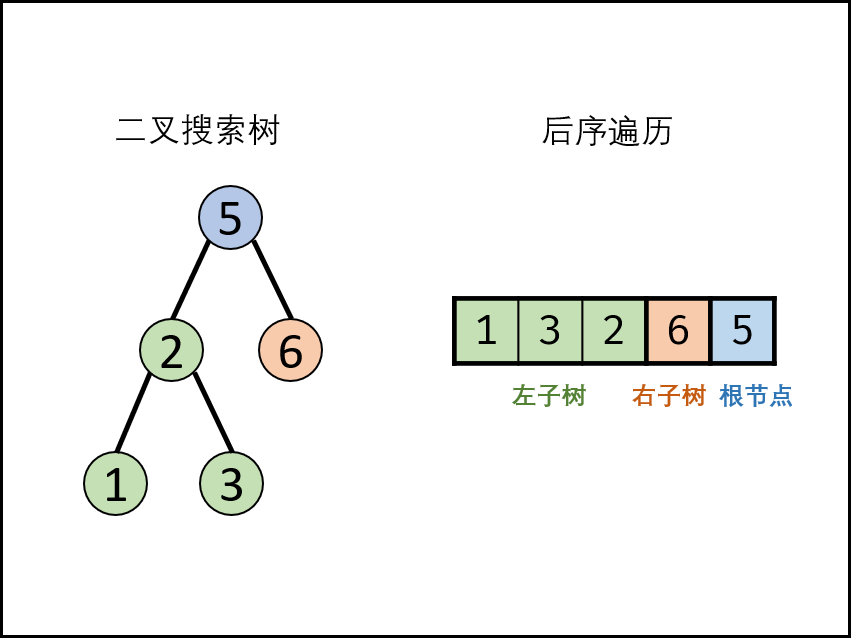
1) 递归分治
根据二叉搜索树的定义,可以通过递归,判断所有子树的正确性(即其后序遍历是否满足二叉搜索树的定义),若所有子树都正确,则此序列为二叉搜索树的后序遍历。
Java-代码🌳
class Solution {
public boolean verifyPostorder(int[] postorder) {
return recur(postorder, 0, postorder.length - 1);
}
boolean recur(int[] postorder, int i, int j) {
if(i >= j) return true;
int p = i;
while(postorder[p] < postorder[j]) p++; //postorder[j] 为 root 值
int m = p;
while(postorder[p] > postorder[j]) p++;
return p == j && recur(postorder, i, m - 1) && recur(postorder, m, j - 1);
}
}
复杂度分析
- 时间复杂度 \(O(N^2)\):每次调用 recur(i,j) 减去一个根节点,因此递归占用 \(O(N)\);最差情况下(即当树退化为链表),每轮递归都需遍历树所有节点,占用 \(O(N)\)。
- 空间复杂度 \(O(N)\):最差情况下(即当树退化为链表),递归深度将达到 \(N\)。
2) 辅助单调栈
后序遍历倒序:[ 根节点 | 右子树 | 左子树 ] 。类似先序遍历的镜像,即先序遍历为 “根、左、右” 的顺序,而后序遍历的倒序为 “根、右、左” 顺序。
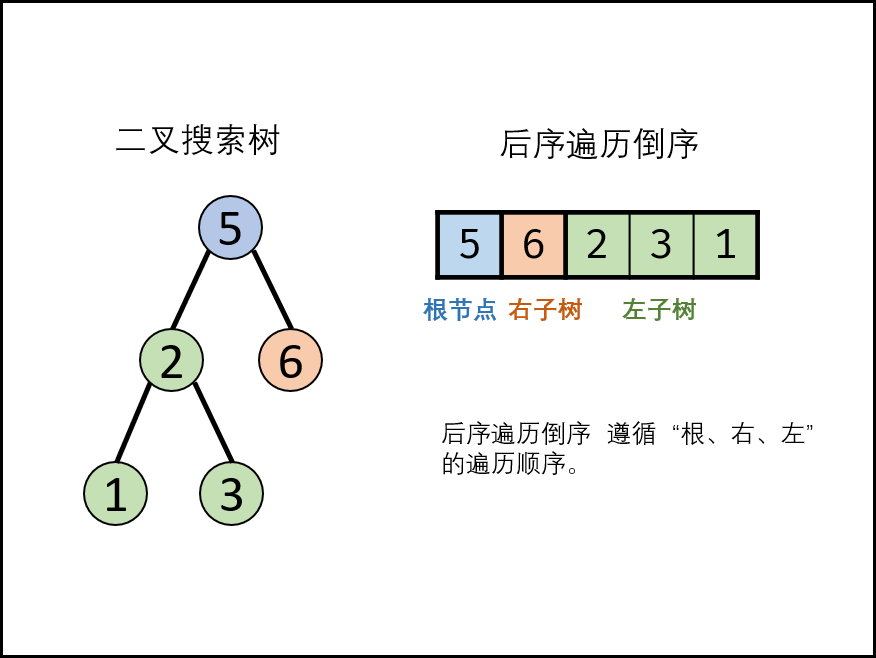
-
设后序遍历倒序列表为 \([r_{n}, r_{n-1},...,r_1]\),遍历此列表,设索引为 i,若为二叉搜索树,则有:
-
当节点值 \(r_i > r_{i+1}\) 时:节点 \(r_i\) 一定是节点 \(r_{i+1}\) 的右子节点。
-
当节点值 \(r_i < r_{i+1}\) 时:节点 \(r_i\) 一定是某节点 root 的左子节点,且 root 为节点 \(r_{i+1}, r_{i+2},..., r_{n}\) 中值大于且最接近 \(r_i\) 的节点(root 直接连接 左子节点 \(r_i\))。
-
-
当遍历时遇到递减节点 \(r_i < r_{i+1}\),若为二叉搜索树,则对于后序遍历中节点 \(r_i\) 右边的任意节点 \(r_x \in [r_{i-1}, r_{i-2}, ..., r_1]\),必有节点值 \(r_x < root\)。
节点 \(r_x\) 只可能为以下两种情况:① \(r_x\) 为 \(r_i\) 的左、右子树的各节点;② \(r_x\) 为 root 的父节点或更高层父节点的左子树的各节点。在二叉搜索树中,以上节点都应小于 root 。
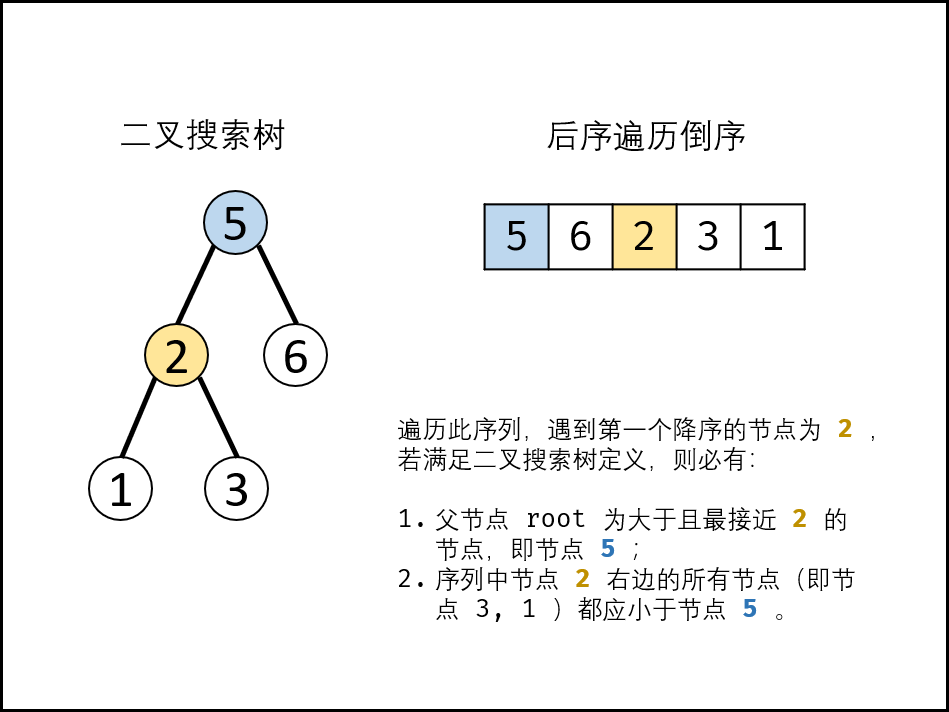
-
遍历 “后序遍历的倒序” 会多次遇到递减节点 \(r_i\),若所有的递减节点 \(r_i\) 对应的父节点 root 都满足以上条件,则可判定为二叉搜索树。
-
根据以上特点,考虑借助单调栈实现:
- 借助一个单调栈 stack 存储值递增的节点;
- 每当遇到值递减的节点 \(r_i\),则通过出栈来更新节点 \(r_i\) 的父节点 root;
- 每轮判断 \(r_i\) 和 root 的值关系:
- 若 \(r_i > root\) 则说明不满足二叉搜索树定义,直接返回 false 。
- 若 \(r_i < root\) 则说明满足二叉搜索树定义,则继续遍历。
Java-代码🌳
class Solution {
public boolean verifyPostorder(int[] postorder) {
Stack<Integer> stack = new Stack<>();
int root = Integer.MAX_VALUE;
for(int i = postorder.length - 1; i >= 0; i--) {
if(postorder[i] > root) return false;
while(!stack.isEmpty() && stack.peek() > postorder[i])
root = stack.pop();
stack.add(postorder[i]);
}
return true;
}
}
复杂度分析
- 时间复杂度 \(O(N)\):遍历 postorder 所有节点,各节点均入栈/出栈一次,使用 \(O(N)\) 时间。
- 空间复杂度 \(O(N)\):最差情况下,单调栈 stack 存储所有节点,使用 \(O(N)\) 额外空间。
剑指 Offer 36. 二叉搜索树与双向链表
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
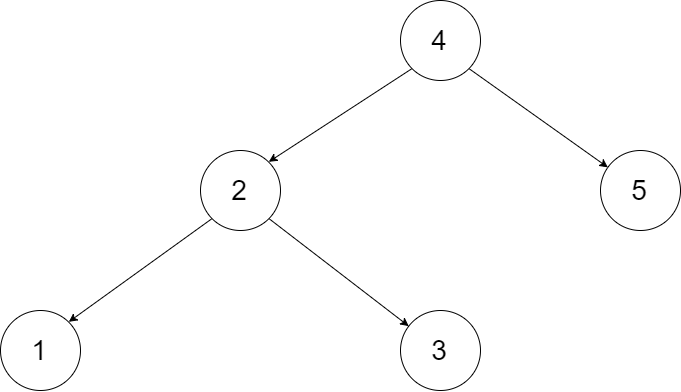
将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。
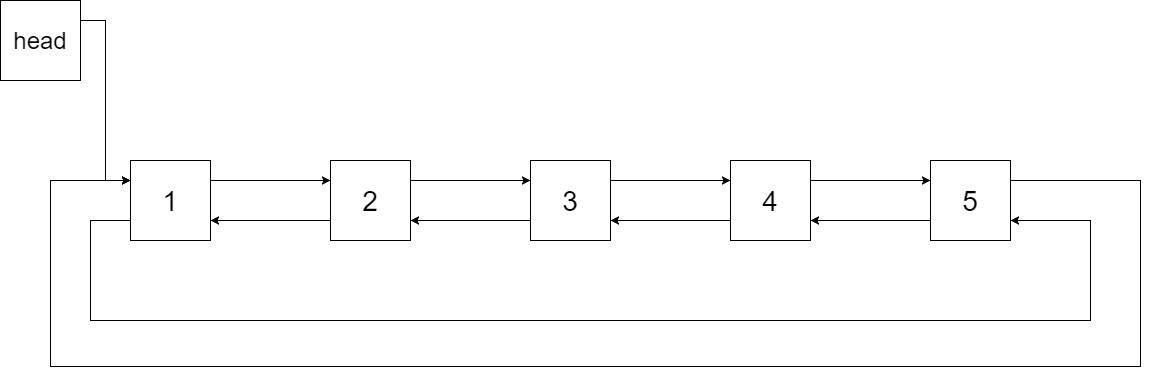
希望可以就地完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
中序遍历
将二叉搜索树转换成一个 “排序的循环双向链表” ,其中包含三个要素:
-
排序链表:节点应从小到大排序,因此应使用中序遍历 “从小到大”访问树的节点。
-
双向链表:在构建相邻节点的引用关系时,设前驱节点 pre 和当前节点 cur,不仅应构建 pre.right = cur,也应构建 cur.left = pre。
-
循环链表:设链表头节点 head 和尾节点 tail,则应构建 head.left = tail 和 tail.right = head 。
使用中序遍历访问树的各节点 cur;并在访问每个节点时构建 cur 和前驱节点 pre 的引用指向;中序遍历完成后,最后构建头节点和尾节点的引用指向即可。
Java-代码🌳
class Solution {
Node pre, head;
public Node treeToDoublyList(Node root) {
if(root == null) return null;
dfs(root);
head.left = pre;
pre.right = head;
return head;
}
void dfs(Node cur) {
if(cur == null) return;
dfs(cur.left);
if(pre != null) pre.right = cur;
else head = cur;
cur.left = pre;
pre = cur;
dfs(cur.right);
}
}
C++-代码🌳
class Solution {
public:
Node* treeToDoublyList(Node* root) {
if(root == nullptr) return nullptr;
dfs(root);
head->left = pre;
pre->right = head;
return head;
}
private:
Node *pre, *head;
void dfs(Node* cur) {
if(cur == nullptr) return;
dfs(cur->left);
if(pre != nullptr) pre->right = cur;
else head = cur;
cur->left = pre;
pre = cur;
dfs(cur->right);
}
};
复杂度分析
-
时间复杂度 \(O(N)\):\(N\) 为二叉树的节点数,中序遍历需要访问所有节点。
-
空间复杂度 \(O(N)\):最差情况下,即树退化为链表时,递归深度达到 \(N\),系统使用 \(O(N)\) 栈空间。
剑指 Offer II 053. 二叉搜索树中的中序后继
给定一棵二叉搜索树和其中的一个节点 p,找到该节点在树中的中序后继。如果节点没有中序后继,请返回 null 。
节点 p 的后继是值比 p.val 大的节点中键值最小的节点,即按中序遍历的顺序节点 p 的下一个节点。树中各节点的值均保证唯一。
1) 中序遍历
为了找到二叉搜索树中的节点 p 的中序后继,最直观的方法是中序遍历。由于只需要找到节点 p 的中序后继,因此不需要维护完整的中序遍历序列,只需要在中序遍历的过程中维护上一个访问的节点和当前访问的节点。如果上一个访问的节点是节点 p,则当前访问的节点即为节点 p 的中序后继。
如果节点 p 是最后被访问的节点,则不存在节点 p 的中序后继,返回 null。
Java-代码🌳
class Solution {
public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
Deque<TreeNode> stack = new ArrayDeque<TreeNode>();
TreeNode prev = null, curr = root;
while (!stack.isEmpty() || curr != null) {
while (curr != null) {
stack.push(curr);
curr = curr.left;
}
curr = stack.pop();
if (prev == p) {
return curr;
}
prev = curr;
curr = curr.right;
}
return null;
}
}
C++-代码🌳
class Solution {
public:
TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
stack<TreeNode*> st;
TreeNode *prev = nullptr, *curr = root;
while (!st.empty() || curr != nullptr) {
while (curr != nullptr) {
st.emplace(curr);
curr = curr->left;
}
curr = st.top();
st.pop();
if (prev == p) {
return curr;
}
prev = curr;
curr = curr->right;
}
return nullptr;
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 \(n\) 是二叉搜索树的节点数。中序遍历最多需要访问二叉搜索树中的每个节点一次。
-
空间复杂度:\(O(n)\),其中 \(n\) 是二叉搜索树的节点数。空间复杂度取决于栈深度,平均情况是 \(O(logn)\),最坏情况是 \(O(n)\)。
2) 利用二叉搜索树的性质
中序后继是节点值大于 p 的节点值的所有节点中节点值最小的一个节点。
利用二叉搜索树的性质,可以在不做中序遍历的情况下找到节点 p 的中序后继。
-
如果节点 p 的右子树不为空,则节点 p 的中序后继在其右子树中,在其右子树中定位到最左边的节点,即为节点 p 的中序后继。
-
如果节点 p 的右子树为空,则需要从根节点开始遍历寻找节点 p 的祖先节点。
将答案初始化为 null。用 node 表示遍历到的节点,初始时 node=root。每次比较 node 的节点值和 p 的节点值,执行相应操作:
-
如果 node 的节点值大于 p 的节点值,则 p 的中序后继可能是 node 或者在 node 的左子树中,因此用 node 更新答案,并将 node 移动到其左子节点继续遍历;
-
如果 node 的节点值小于或等于 p 的节点值,则 p 的中序后继可能在 node 的右子树中,因此将node 移动到其右子节点继续遍历。
由于在遍历过程中,当且仅当 node 的节点值大于 p 的节点值的情况下,才会用 node 更新答案,因此当节点 p 有中序后继时一定可以找到中序后继,当节点 p 没有中序后继时答案一定为 null。
Java-代码🌳
class Solution {
public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
TreeNode successor = null;
if (p.right != null) {
successor = p.right;
while (successor.left != null) {
successor = successor.left;
}
return successor;
}
TreeNode node = root;
while (node != null) {
if (node.val > p.val) {
successor = node;
node = node.left;
} else {
node = node.right;
}
}
return successor;
}
}
C++-代码🌳
class Solution {
public:
TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
TreeNode *successor = nullptr;
if (p->right != nullptr) {
successor = p->right;
while (successor->left != nullptr) {
successor = successor->left;
}
return successor;
}
TreeNode *node = root;
while (node != nullptr) {
if (node->val > p->val) {
successor = node;
node = node->left;
} else {
node = node->right;
}
}
return successor;
}
};
复杂度分析
-
时间复杂度:\(O(n)\),其中 \(n\) 是二叉搜索树的节点数。遍历的节点数不超过二叉搜索树的高度,平均情况是 \(O(logn)\),最坏情况是 \(O(n)\)。
-
空间复杂度:\(O(1)\)。
面试题 04.09. 二叉搜索树序列
1) xx
Java-代码🌳
C++-代码🌳



 浙公网安备 33010602011771号
浙公网安备 33010602011771号