操作系统(二)—— 操作系统内存管理(上)
概述
程序都需要被加载到内存中才可以运行,在远古时代^_^,程序的内存只有非常非常小的几kb,如果要运行的程序很大,大到超过了内存,而且还想要运行这样的程序,要怎么做呢?如果在内存中同时运行几个程序,如何确保某个程序不会修改别的程序的内存中的值呢?以上的问题总结下来基本就三大核心问题:
- 进程之间如何隔离
- 内存使用低效的问题
- 程序地址空间重定向的问题
这些问题操作系统都已经解决了,下面就介绍一下操作系统是如何解决这些问题的。
虚拟地址空间
在远古时期,操作系统和应用程序都直接根据物理地址来寻址,这样如果应用程序在程序中把某个地址给恶意修改了,那操作系统很容就会被破坏,除了这个问题之外,多个应用程序同时运行也同样具有这样的问题,这个问题的根源就是程序所在内存空间没有隔离,那内存就那一块,采用物理隔离不太现实,所以只能采用虚拟的方式,也就是虚拟地址空间。每个进程都有一份自己独立的地址空间,这份地址空间(虚拟地址)可以相同,但是由于虚拟地址空间和物理地址空间的映射位置不同,故不会发生多个进程同时修改同一个物理地址的问题。
由于编写程序时,访问数据和指令的地址很多是固定的(这段话来自《程序员的自我修养》,不是很明白),而程序装载到内存中时的位置是不确定的,所以就需要程序重定向,采用虚拟地址可以很好的解决这个问题,因为虚拟地址空间就不存在重定位的问题。
采用虚拟地址基本解决了上面提到的第一个和第三个问题,但是第二个问题如何解决呢?且看下一章节。
分段
举个例子,内存容量大小为256MB,程序A需要200MB,程序B需要50MB,程序C需要100MB,如果现在同时运行A和B,ok。如果这个时候C也想运行,有一个办法是把内存中的A先保存到磁盘上,然后就可以腾出来空间供程序C运行,但是这样做非常低效,因为把一个200M的数据复制到磁盘还是很浪费时间的,那有没有比较高效的方式,起初,计算机科学家是采用分段的方式来解决这个问题。
分段实现方法如下:
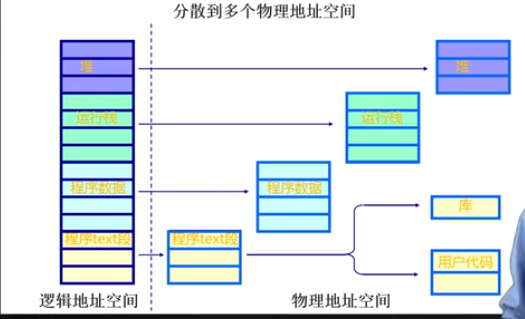
(图片来源:清华大学操作系统公开课)
从上图可以看出,在逻辑地址空间,程序的堆、栈、程序数据等是连续的,而映射到实际的物理内存的时候并不连续,而是每个段是分开的,下面看一下实际的逻辑视图。
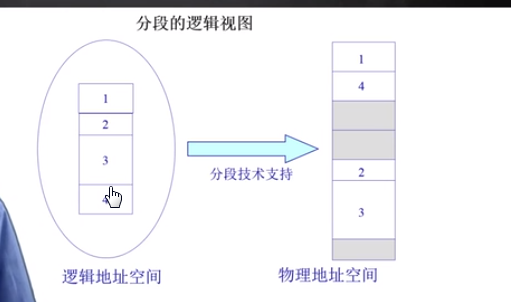
(图片来源:清华大学操作系统公开课)
这个图很清晰的可以看出来,左边的额1,2,3,4表示逻辑空间的段,右边是每个段在物理空间的实际存储。
寻址方法
上面已经明白了分段的方式,那如何进行寻址呢?这里介绍一种硬件寻址的方法。
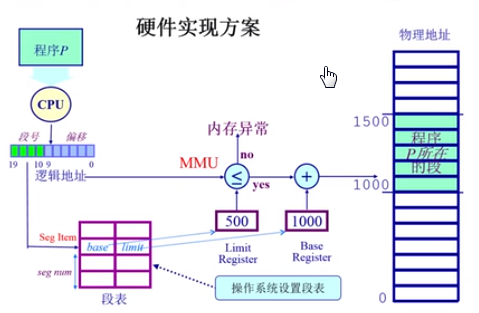
(图片来源:清华大学操作系统公开课)
上图的总过程先介绍一下,然后再对里面的一些细节解释一下。
CPU内部有一个内存管理单元叫做MMU,里面保存了经常被访问的段号,当需要访问某个段中的地址的时候,cpu先去MMU中寻找对应的段号,然后去内存的段表中查找当前段的最大长度,之后判断需要寻找的地址在段中的偏移是否大于限制的大小,如果小于,ok,就直接把虚拟地址的地址值加上一个固定的偏移量,图中是1000,就获得物理地址的值了。如果需要访问的地址的偏移量大于段的限制长度,就抛出异常,因为访问到非法的地址。
相关概念解释如下:
MMU:中文名是内存管理单元,有时称作分页内存管理单元(英语:paged memory management unit,缩写为PMMU)。它是一种负责处理中央处理器(CPU)的内存访问请求的计算机硬件。
段表:一般存放在内存中,由操作系统维护,每个进程有一个独立的段表,是一个二维结构,第一个维度为段号,第二个维度为段内偏移量,段号是每个段的标识,段内偏移量是该段的长度。
逻辑地址:是虚拟的,实际上并不存在,程序运行使用的地址。
物理地址:实际物理内存的地址,逻辑地址会和物理地址存在一个映射关系。
总结
分段的方式,在传统的架构中还有使用,现代计算机中基本已经没有使用了,原因是这种方式分的粒度还是太大,比如,内存不足的时候,把某个分段拷贝到磁盘上,需要拷贝的量还是很高,效率太低,所以要进一步细分,也就有了分页技术,这个分的粒度更低,一般来说每一页只有4kb。
分页
分页的基本方法是人为的把地址空间等分为大小相同的页,现代的pc机基本都是使用4kb为一页,物理空间一页叫做页帧,逻辑空间的页就叫做页,两者大小相同,分页的好处是,当要运行一个程序的时候,操作系统没有必要把该程序的全部代码和数据加载到内存中,而是把需要的页放到内存中,随着程序的运行,可能会需要新的数据,内存中不存在,这个时候就从磁盘上把那些页读到内存中,如果内存空间不足,就把之前用过的页先从内存中存到磁盘上,把这个空间腾出来,这样就可以解决内存不足的问题,举个例子,需要运行的程序所需的空间是1GB,而实际的内存只有512MB,通过刚刚讲的页面置换的方法,就可以正常运行了。
上面简要把整个过程叙述了一下,下面具体介绍一下。
页帧
页帧是指物理地址中的一页。物理地址的表示方法是使用一个二元组(f,o),其中f表示页号,o表示页内偏移量,物理地址的计算方法为:2^S * f + o,S表示表示页内偏移量所使用的计算机位数,由于一般每一页的大小是4kb,也就是4096个字节,所以需要212位来表示页内偏移量。
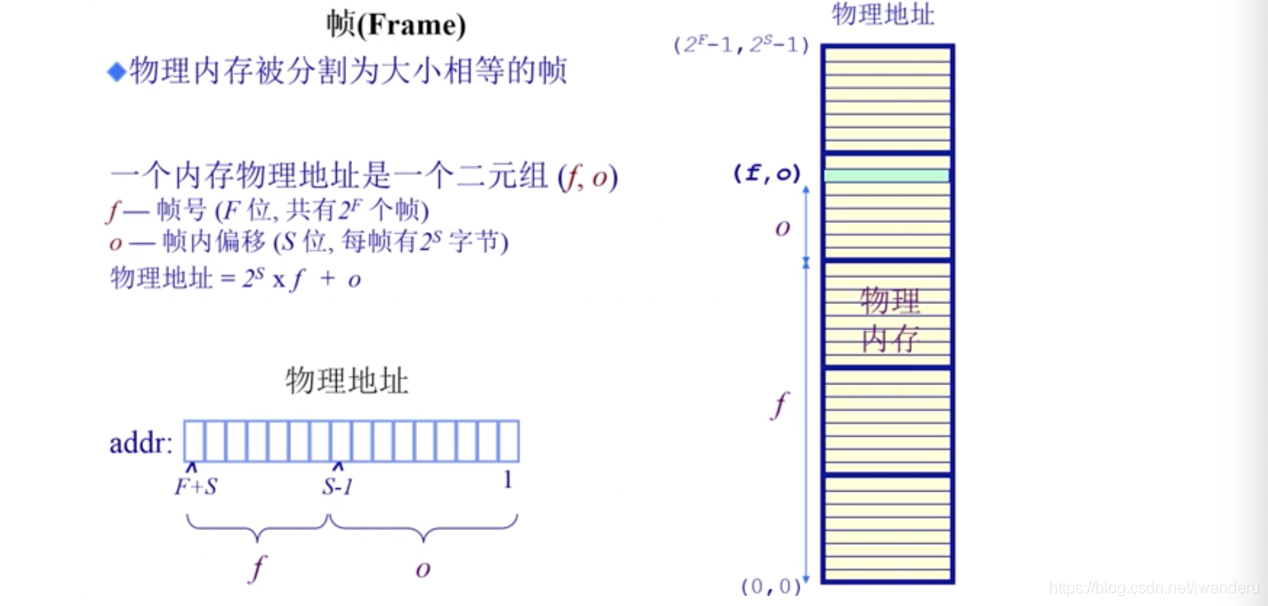
(图片来源:清华大学操作系统公开课)
举例如下:
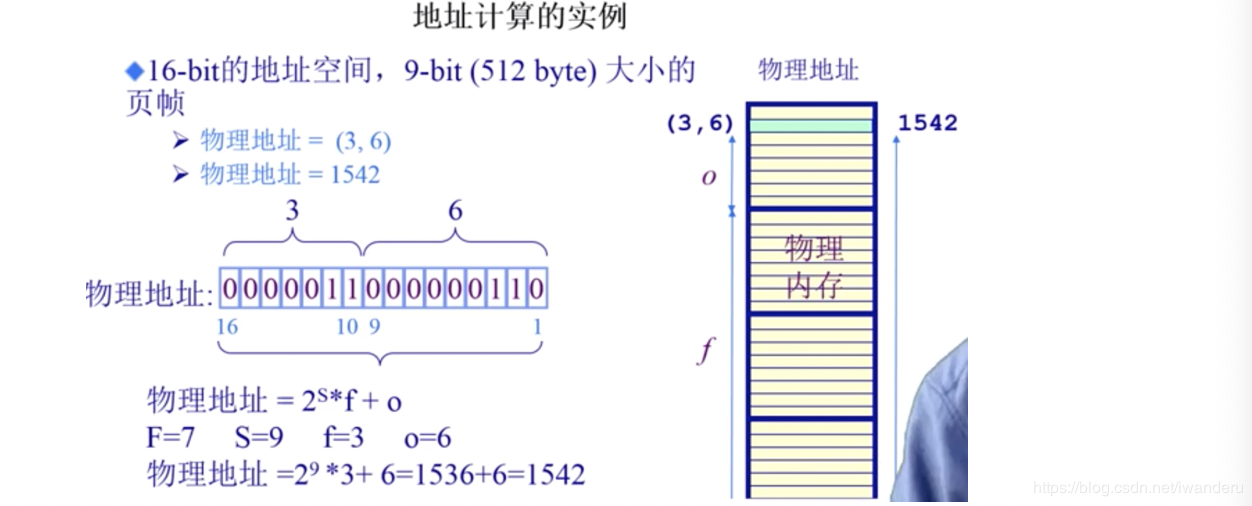
(图片来源:清华大学操作系统公开课)
这个例子中,使用的是16位地址空间,其中每一页的大小为512byte,并不是上面说的4kb,所以页内偏移量就是512byte,对应的位也就是9位,因为2^9 = 512,所以S = 9,根据公式就很容易计算出来实际的物理地址。
页
页的地址计算方法和页帧的相同,需要注意,页号不一定等于页帧号,但是页内偏移量 = 页帧内偏移量。
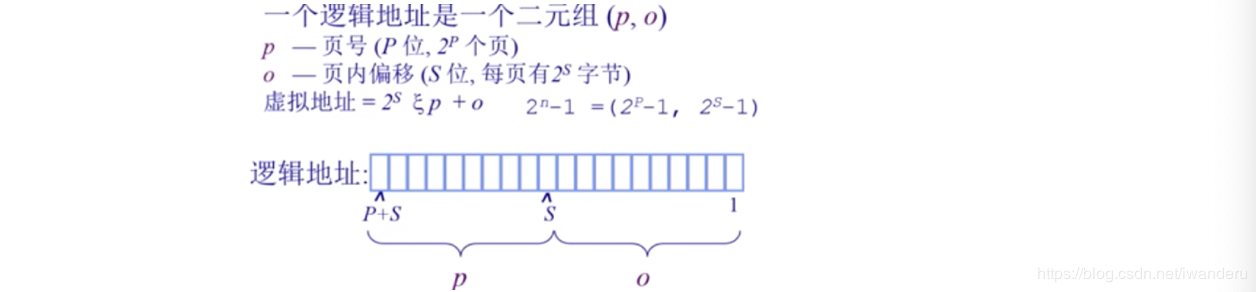
这里表示方法中有点和帧不同,就是这里的p,在帧中这里使用f进行表示。
页寻址方法
程序在运行的时候其实是已知虚拟地址的,那现在的问题就是如何根据虚拟地址找到物理地址,由于页和页帧的页内偏移量相同,所以这个问题就变成了寻找虚拟地址的页号和物理地址的页号的映射关系,保存这个映射关系的是页表,下面先介绍一下页表。
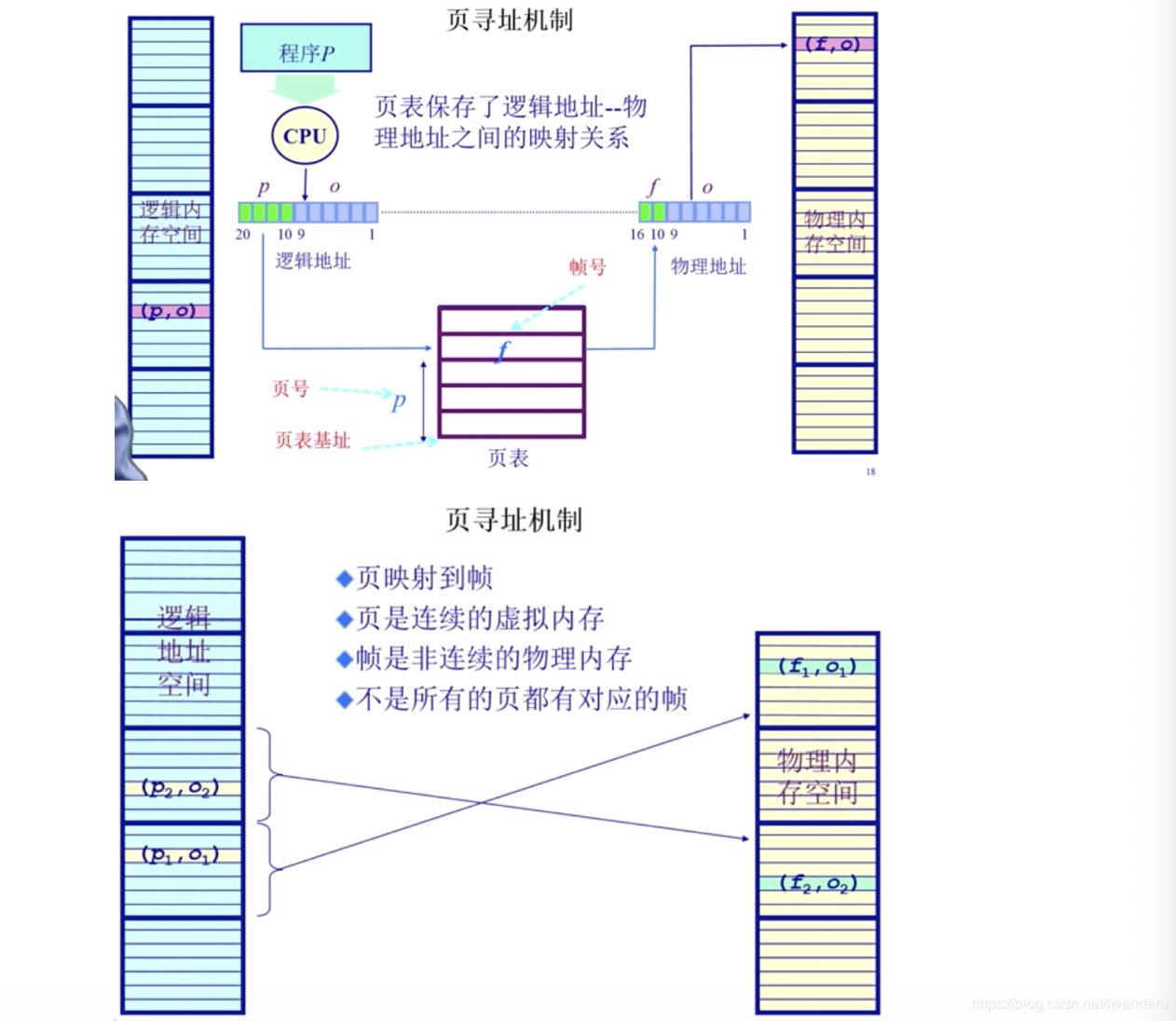
页表
先看一个典型地页表的结构

(图片来源:现代操作系统)
页框号:其实就是上面说的页帧号
在/不在位:表示该页帧在物理内存中是否存在,如果不存在,当访问这一页的时候,会抛出一个缺页中断,操作系统会处理。
保护位:其实就是我们说的权限,比如linux中权限分为读、写、执行,最简单的表示方法就是只有一位,那就只能表示两种状态,比如,读和写。
访问位:无论操作系统访问改页是读还是写,都会修改该位,这个位在后面介绍页面置换算法时非常重要。
修改位:当页面发生写操作的时候,需要修改该位,因为一旦该页被修改,就变成了脏页,如果需要和磁盘上的页发生置换,就需要先把该页保存到磁盘上,如果没有修改,其实可以直接把该页丢弃,把内存空间腾出来。
高速缓存禁止位:不太明白作用
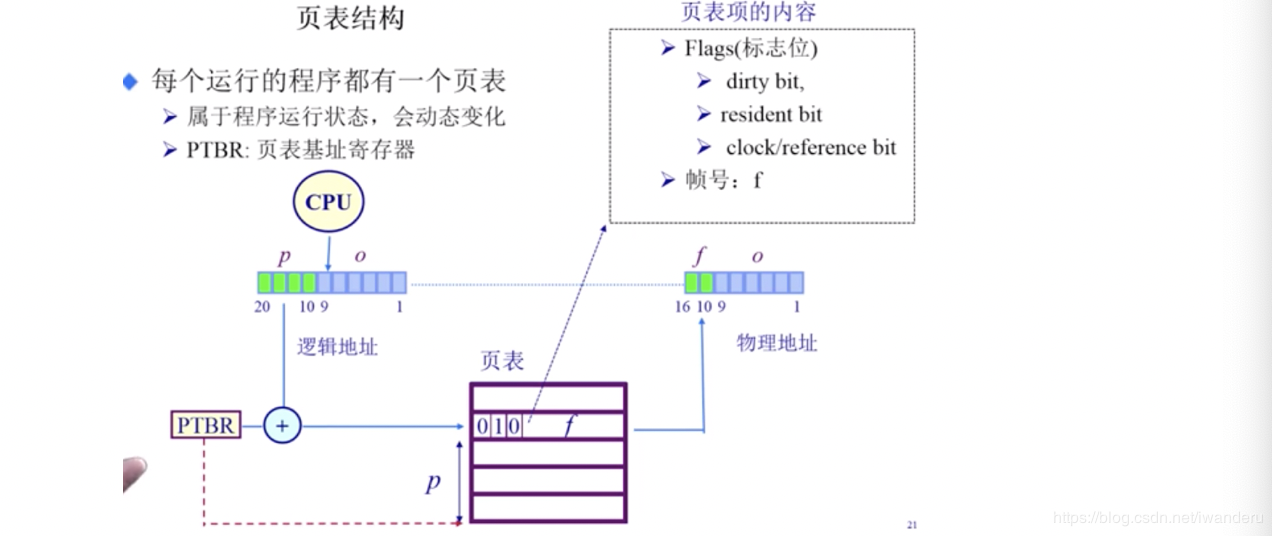
(图片来源:清华大学操作系统公开课)
上图基本把寻址的过程清楚的表达出来了,根据逻辑地址的p查找页表,然后查看标志位,图中只画出来三个标志位,分别为dirty bit(修改位)= 0,resident bit(在不在位) = 1,clock/reference bit(访问位) = 0,由于在不在位为1表示该页在物理地址中不存在,所以如果要访问该页会抛出一个缺页中断。
上面把寻址的原理介绍完之后,接下来一个重要的问题就是效率问题,上面的方式cpu每次读取一个地址的数据,需要访问内存两次,第一次访问页表查找物理地址的位置,第二次访问物理地址取数据,这种方式是效率很低的。除了需要两次访问内存的问题,还有一个空间占用的问题,假设一个64位系统,每页大小是4kb,也就是4096 = 2^12,那还剩余52位,除去上面介绍的在不在位、访问位、修改位等,应该还会剩余45位,也就是说会有2^45个页,如果每个程序一个页表,那可想而知会有多大,最起码cpu是装不下。
ok,问题介绍完了,下面就看解决方案,针对两次访问内存的问题,采用使用TLB的方案解决,针对页表过大的问题,采用多级页表或者倒排页表解决,下面就介绍一下每种解决方案的细节。
TLB
TLB(Translation Lookaside Buffer)转换检测缓冲区,是存在于MMU中的一种小型硬件设备,可以将虚拟地址直接映射到物理地址,其中包含少量的表项(一项其实就是页表的一条记录),一般小于256条,如下图所示。
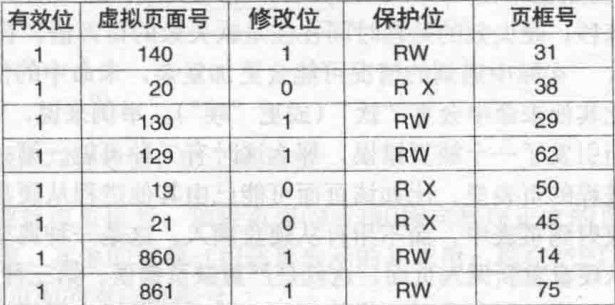
(图片来源:现代操作系统)
寻址的过程是这样的,cpu先去TLB查找,如果命中,就直接使用TLB中的物理地址,而不用再访问内存,如果没有命中,就需要去内存中查找,然后把查找的结果放入TLB中,但是这是TLB是满的,需要先从中剔除一条,剔除的这条并不能直接丢弃,需要把他的访问位和修改位更新到内存的页表中。以上整个过程都是通过硬件完成的,除非访问页的时候,发现在不在位不在,才需要操作系统介入,把对应的页从磁盘读到内存中。但是在有些硬件上TLB管理是操作系统完成的,在《现代操作系统》中有介绍,当TLB中的表项大到一定程度时(比如64个表项),TLB软件管理就会变的足够有效,这样就可以获得一个简单的MMU,这就为CPU芯片上的高速缓存及其他改善性能的设计腾出空间。
多级页表
多级页表,有点类似于mysql数据库Innodb引擎的索引结构,但是比索引结构使用B+树简单很多,使用多级页表并不能减少访问的时间,反而因为分级之后,查询次数变多,性能变差,但是这样做却可以节省空间,是一种时间换空间的思路,至于为什么可以节省空间,看一下下面的例子就明白了了。
假设在32位系统中,一级页表占用10位,也就是2^10 = 1024。由于2^32 = 4GB,所以一级页表的每个表项负责整个内存的4M的空间,因为4M * 1024 = 4GB,二级页表页占用10位,那偏移量占用12位,也就是2^12位,也就是4kb,所以每页的大小为4kb。具体看下图。
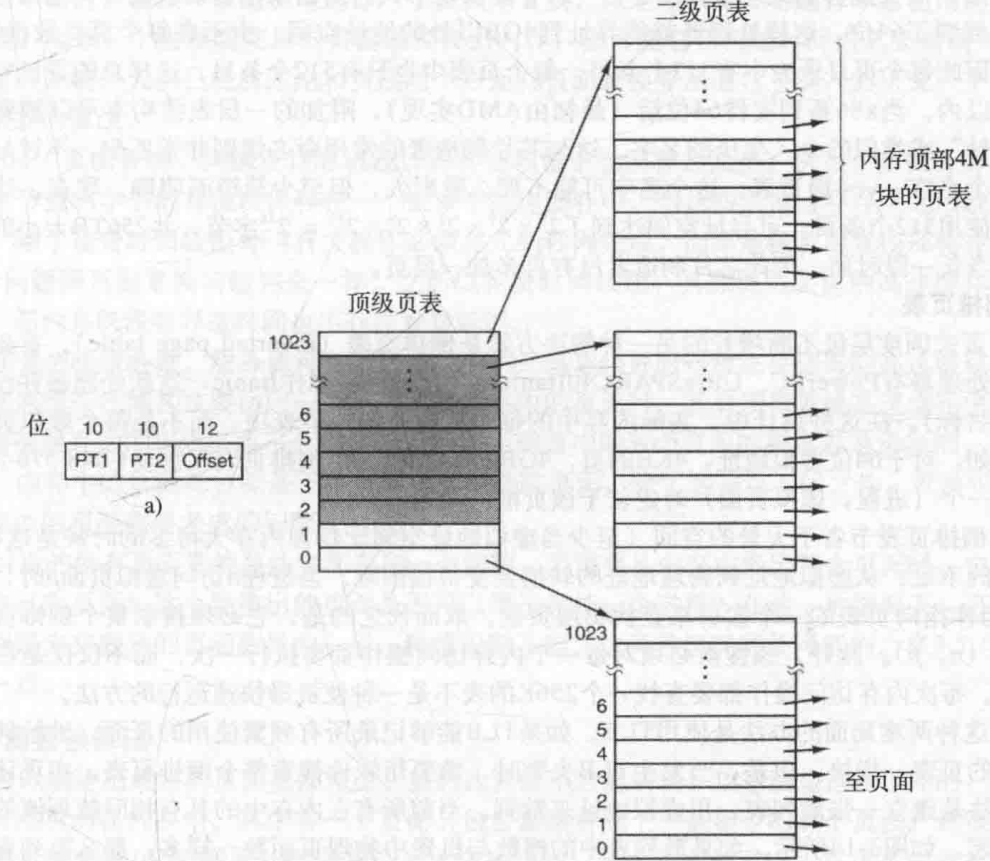
图片来源:现代操作系统
在一级页表中也会存在一个在不在位,如果一级页表的在不在位为不存在,那就没有必要搞一个二级页表和这个表项相对应,这样就可以节省很多空间,举个例子,程序A运行代码段占用空间4M,数据占用4M,4M的堆栈,那在一级页表中只有3个表项的在不在位为存在,只有这三个有对应的二级页表就可以了。这就是上面说这是一种以时间换空间的做法的原因。
细心的胖友可能会问,不使用多级页表,只使用一个页表可不可以做到节省空间,答案是不能,看多级页表的1级页表就知道,即便是这个表项没有被使用,也要存在,并且需要一个在不在位来标识。
倒排页表
这个思想很牛逼,但是实现很困难,为什么说思想很牛逼,大家看上面的实现方式,逻辑空间是不受限制的,如果内存是4G,那逻辑空间的寻址就是4G,如果每个进程都这样搞,那内存中为了给这个虚拟空间做映射建立的页表才会占用很多的空间。那思路能不能反过来,通过物理地址来找逻辑地址,因为物理地址只有4G,那页表的大小可以很容易确定下来,而且逻辑地址的大小已经没有意义,无论逻辑地址多大,最终一定会和物理地址映射,那就一定会落到实际的4G物理内存中。下面看一下如何实现。
实现方式有两种,第一种是硬件的实现方案,没看懂,这里就不介绍了,介绍第二种,基于散列表(hash表)实现的。
看过java中的HashMap实现原理的都知道,HashMap就是使用散列表实现的,通过搞一个数组来确定桶的位置,之后在每个桶上挂一个链表,倒排页表也是这个思路,计算每个进程逻辑地址的hash值,之后确定对应的桶的位置,然后挂到桶上,桶的长度就是分页的个数,这里多个进程的虚拟页可能会映射到同一个物理页框,发生hash冲突,发生冲突最大个数也就是一页的大小。举个例子32位系统,2^20表示页面的个数,2^12 = 4kb,表示一页的大小,总内存大小是4GB,那对应散列表的桶的个数就是2^20个,每个桶发生hash冲突的最大值为2^12。
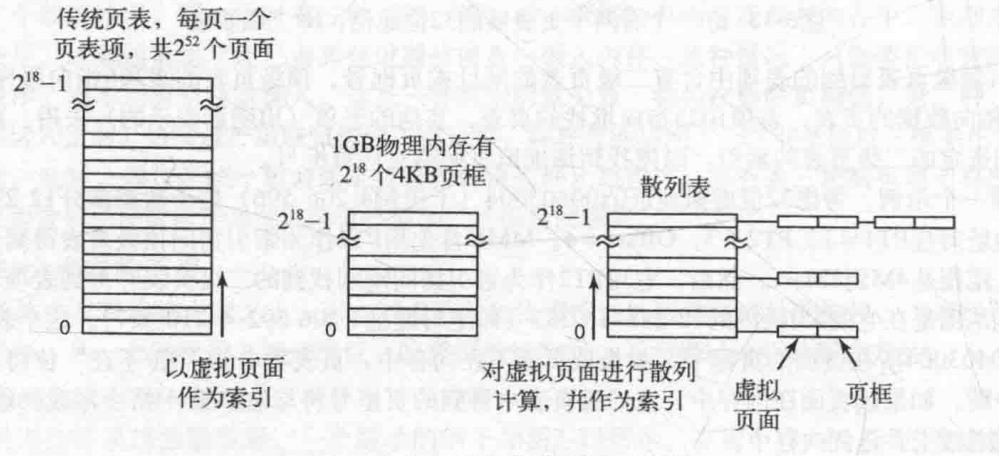
图片来源:现代操作系统
图中是用1GB内存来举例的,2^18表示页面的个数,也就是正常页表的表项的个数,2^12表示一页的大小。最左边的图就是前面介绍的正常的页表,最右边的就是散列表。
总结
本文主要介绍了操作系统内存管理,介绍了为什么使用虚拟地址,使用虚拟地址之后如何进行寻址,以及如何优化寻址过程,本来打算把页面置换算法一次性介绍完,但是觉得文章写得太长,所以就下一篇介绍。

参考:
清华大学操作系统公开课
《现代操作系统》
《程序员的自我修养》



