堆排序
本文参考:
推荐大家看这两篇文章,文章中图画的非常好,我觉得作者非常用心,相比之下我就比较水了,大家可以把我的代码作为一个参考,其他的看看上面那两篇文章就可以了
概述
堆排序,听名字好像和java中的堆空间有点关系,但其实这两个兄弟一点关系也没有,参考:堆内存和数据结构堆之间的关系是什么?,第一次听说这个排序算法的时候,确实很懵,因为连什么是堆都不知道,然后当知道了堆的概念之后,这个排序算法交换来,交换去,也挺麻烦的,总之,这个排序算法在常见的排序算法中算最复杂的,要想搞懂这个排序算法要先搞明白下面几个问题:
- 堆数据结构是什么样子的
- 什么是完全二叉树
- 堆使用什么数据结构存储
- 完全二叉树有哪些性质,比如已知完全二叉树节点个数,怎么求叶子节点个数(如果你像我一样有很多疑问,你一定会想知道怎么证明这些性质,^_^)
虽然,上面两篇文章中已经介绍了上面3个问题(第三个问题没证明),我这里还是简略的写一下,谁让别人写的永远是别人的,自己学会了写出来才是自己的呢。
堆数据结构是什么样子的
堆:首先,堆是一颗完全二叉树,其次,堆分为大顶堆和小顶堆
- 大顶堆:完全二叉树的父节点的值大于或者等于子节点的值
- 小顶堆:完全二叉树的父节点的值小于或者等于子节点的值
什么是完全二叉树
若设二叉树的深度为k,除第 k 层外,其它各层 (1~k-1) 的结点数都达到最大个数,第k 层所有的结点都连续集中在最左边,这就是完全二叉树。
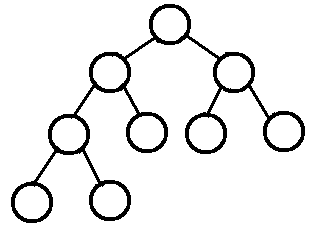
或者
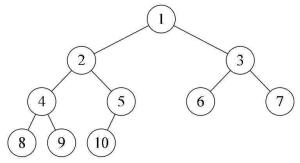
这两个都是完全二叉树。
堆数据使用什么数据结构存储的
堆由于是完全二叉树的结构,那就可以使用数组存储,只要采用层序遍历方式即可,层序遍历就是一行一行的遍历,例如上面的图用数据使用数组存储如下

完全二叉树有哪些性质
大家可以参考这篇文章:二叉树的五大性质及证明
那堆排序所要使用的最重要的完全二叉树的两个性质
性质一:
满二叉树是一种特殊的完全二叉树,假设其深度为h,则其节点个数为2^h - 1
证明:
满二叉树节点个数计算为2^0 + 2^1 + 2^2 + 2^3 +...+ 2^h其实是一个等比数列,等比数列求和公式a1(1-q^h)/(1-q),由此得证
性质二:
假设父节点编号为i,则左子节点编号为2i,右子节点标号为2i+1,注意(根节点编号从1开始)
证明:
假设父节点位于第h层的第m个节点,根据性质一可以得出如下结论:
父节点编号:i = 2^(h-1) - 1 + m 公式1
左子节点编号为: 2^h - 1 + 2(m-1) + 1 公式2
右子节点编号为: 2^h - 1 + 2m 公式3
由公式一可以推导出来如下结果:
公式2 = 2i
公式3 = 2i + 1
性质三:
完全二叉树第一个非叶子节点编号为total/2,其中total为节点总数
证明:
完全二叉树最后一个元素编号为total,则其父节点为最后一个非叶子节点,根据性质二可以直接证明
总结:第二个和第三个性质对于写堆排序的程序非常重要,注意上面公式中第一个元素的编号为1,但是如果使用数组存储,数组的第一个元素下标往往是0,所以上面公式都要做相应的调整,调整如下:
- 如果父节点的标号为i,左子节点编号为2i+1,右子节点编号为2i+2
- 第一个非叶子节点的编号为total/2 - 1
什么是堆排序
堆排序分为两步
第一步:先把待排序数组调整成一个堆,如果是从小到大排序,调整成大顶堆,如果是从大到小排序,调整成小顶堆
第二步:排序,假设从小到大排序,过程如下
- 第一次调整,把堆顶元素(最大的元素)和堆尾(最后一个叶子节点)元素交换,这时,对于排序来说,堆尾元素的位置就是最终的位置了,之后重复第一步(注意这里要把刚刚最后一个元素排除在外,因为如果不排除在外,这个元素又跑到堆顶了)
- 第二次调整,经过第一次调整,堆顶元素就是次大的元素了,这里把它和堆尾元素的前一个位置元素交换(因为第一次调整时放到堆尾的是最大的,这次调整堆顶的元素是次大,所以放到最大的前一个位置)
- ..........
- 就这样一直调整,直到整个是有序的
看过上面两篇文章的朋友可能会看到这么一句话,排序的过程中,不断减小堆的大小,直到把堆的大小减为一个元素,其实这句话的意思就是堆顶的元素是堆中最大的元素,如果把这个元素放到堆尾的正确位置,那堆的大小就减一,就这样不断的减,最后堆的大小就变成了一,就是这个意思(这个当时我看的时候有些不明白,所以这里提了一下)
如果看我文字叙述的朋友看的不是很明白,估计很难明白,^_^,因为怎么把堆调整成大顶堆,我没有写,大家看上面两篇文章吧,那里面有图,应该容易明白一点。
代码
/** * @author: steve * @date: 2020/7/8 14:30 * @description: 堆排序 */ public class HeapSort { public static int array[] = {72,6,57,88,60,42,83,73,48,8}; // public static int array[] = {2,1,3,0}; public static int len = array.length; /*** *@Description 堆排序 *@Param [] *@Return void *@Author steve */ public static void heapSort(){ //《1》 //从第一个非叶子节点开始,这一步非常关键,要从下往上构建堆结构 //这里可以思考一个问题:为什么第一个非叶子节点是len/2 - 1 for (int i = len/2 -1; i >= 0; i--) { adjustHeap(i,len); } for (int i = 0; i < len; i++) {
//《2》 //思考这里为什么是len-1-i,因为堆排序的实质其实就是逐渐减少树的大小 //怎么减小呢?就是把堆顶(堆中最大的值)的元素放到堆的末尾(注意这个末尾,是最大的在最末尾,次大的在最大的前一个位置。。。) swap(0,len-1-i); adjustHeap(0,len-1-i); } } /*** *@Description 调整堆结构 *@Param [] *@Return void *@Author steve */ public static void adjustHeap(int i,int len){ //子节点,这里也可以思考,为什么是这个公式 int child1 = 2*i + 1; int child2 = 2*i + 2; int large; while (child1 < len || child2 < len){ //使用这个双重判断的原因就是可能child2=len,但是child1<len的情况 if (child1 < len) { if (child2 < len) { //找出两个子节点中值较大的一个 if (array[child1] > array[child2]){ large = child1; }else { large = child2; } }else { large = child1; } if (array[i] < array[large]){ //这里其实可以不用交换,直接把子节点的值赋值给父节点就可以了 //这里是测试,为了省事,直接交换了 swap(i,large); i = large; }else { break; } } child1 = 2*i + 1; child2 = 2*i + 2; } } public static void swap(int i, int j){ int temp = 0; temp = array[i]; array[i] = array[j]; array[j] = temp; } public static void main(String[] args) { heapSort(); for (int i = 0; i < len; i++) { System.out.println(array[i]); } } }
解释一下代码中标红的地方
《1》处:这里的i = len/2 -1,就是从第一个非叶子节点开始调整,因为我代码是用父节点和子节点进行比较,然后调整堆的结构,因为叶子节点没有子节点,所以没法调整,所以这里是从第一个非叶子节点。看到这里,估计有的胖友会有疑问,既然是要有子节点才调整,为什么不从根节点开始调整呢?其实不是不可以,而是如果这样做会比较麻烦,如果从第一个非叶子节点开始,每次只需要和下层的元素比较大小就可以了,但是如果是从根节点开始,你就既需要向上比较,又需要向下比较。
《2》处:无论是在交换的方法中还是在调用调整堆的方法中都有一个参数是len-1-i,这个参数作用其实就是上面解释的,逐渐减小堆的大小,直到把堆的大小减小为1,而第一个参数0就表示每次就把堆顶的元素放到堆尾(注意这里堆在变小,所以堆尾并不是指数组的最后一个元素)
结语
写了好多博客,都是自己怎么想就怎么写的,最近比对了下大佬写的博客,发现真正的大佬写的文章都是非常简洁,非常清晰的,只有菜鸟才会把一个简单的概念说的非常复杂,而且真正的大佬文章中使用文字表述不清的地方都是画图演示整个的过程的,以后要多学习



