归并排序
本文参考:图解排序算法(四)之归并排序,大家看这篇文章就够了,不用看我的文章,我的文章没他写的好
概述
前几篇文章,写了快速排序,希尔排序,这两种排序算法都是使用某种方法把数组分成几个部分,然后在每个小的部分进行排序,之后再对整体进行排序,不过快速排序和希尔排序的分段都不彻底,那什么是彻底的呢?就是直接把数组的每个元素分成一组,而一个元素自然是有序的,然后再两两合并,最后就可以实现整个数组的排序。
核心思想
其实在概述中已经说了,归并排序就是先分,再合,在合并的时候对要合并的两个小片段进行排序,时间复杂度为(O(nlogn)),还不错,而且很稳定,不像快速排序和希尔排序,在最坏的情况都要O(n2),好啦,下面通过一个例子来讲解什么是归并排序。
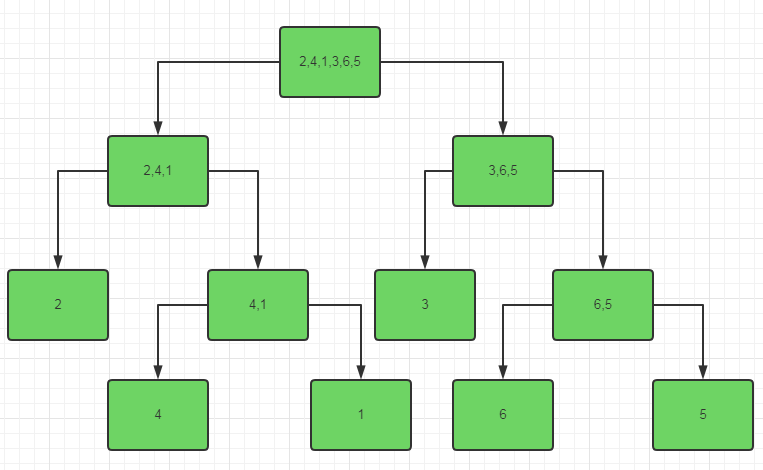
举例:2,4,1,3,6,5
要求:使用归并排序对数组进行排序
拆分过程如下
- 将数组分成两组【2,4,1】,【3,6,5】
- 再分别对两组数据进行拆分,分为四组【2】,【4,1】 【3】,【6,5】
- 继续分,一定要分成一个一个的元素,分为【2】 【4】,【1】 【3】 【6】,【5】
以上的过程用二叉树表示就是如下:
合并过程如下
从树的最底层开始合并,在合并的时候比较4和1的大小,合并成【1,4】,之后再把【2】和【1,4】合并成【1,2,4】,这是合成左子树的,然后把右子树的也合并了,最后在合并左右子树的结果。。。就这样下去就可以实现排序
上面哔哔叭叭哔哔叭叭那么多,看的是不是dan疼(女生请不要对号入座^_^,估计也没有女生)
代码实现
这个代码实现拆分的过程采用递归做的,代码说复杂也复杂说简单也简单,反正我是一开始是自己想,想了半天想了一个思路,后来否定了,看了看大神的文章,发现没有想错,后面的都是自己实现的,也许不是最好的方式,大家姑且看吧
/** * @author: steve * @date: 2020/7/7 11:47 * @description: 归并排序 */ public class MergeSort { public static int array[] = {72, 6, 57, 88, 60, 42, 83, 73, 48, 8, 1}; // public static int array[] = {6, 75,8,14}; //临时数组,用于作为两个有序数组合并的中间数组 public static int temp[] = new int[array.length]; /*** *@Description 递归实现把数组分成小块 *@Param [start, end] *@Return void *@Author steve */ public static void mergeSort(int start, int end){ int mid = (end + start)/2; //下面这个打印可以看出来自己递归有没有问题,大家自己写的时候也可以这样打印出来 // System.out.println(start+"-------"+end); if (end > start){ //左边归并排序 mergeSort(start,mid); //右边归并排序 mergeSort(mid+1,end); } merge(start,mid,end); } /*** *@Description 执行合并的方法,自己想的一个,可能有些复杂 *@Param [start, mid, end] *@Return void *@Author steve */ public static void merge(int start, int mid, int end){ // System.out.println(start+"==="+mid+"==="+end); //游标是为了控制插入临时数组的位置 int cursor = start; int i = start; int j = mid+1; while(i <= mid || j <= end){ if (i <= mid && j <= end){ if (array[i] <= array[j]){ temp[cursor] = array[i]; i++; cursor++; }else { temp[cursor] = array[j]; j++; cursor++; } }else { //这个else的作用就是当要合并的两部分,其中一部分已经全部插入到临时数组,另一部分还有剩余的 //直接将剩余部分插入临时数组,不用比较 if (i <= mid){ temp[cursor] = array[i]; i++; cursor++; } if (j <= end){ temp[cursor] = array[j]; j++; cursor++; } } } System.arraycopy(temp,start,array,start,end-start+1); // for (int k = 0; k < array.length; k++) { // System.out.println(array[k]); // } } /*** *@Description 测试System.arraycopy()函数的功能 *@Param [] *@Return void *@Author steve */ public static void arraycopy(){ int test1[] = {1,2,3}; int test2[] = {2,3,4}; System.arraycopy(test2,1,test1,1,1); for (int i = 0; i < test1.length; i++) { System.out.println(test1[i]); } } public static void main(String[] args) { mergeSort(0,array.length-1); //单独测试merge的功能有没有问题 //// merge(0,0,1); for (int i = 0; i < array.length; i++) { System.out.println(array[i]); } // arraycopy(); } }
总结
在文章的开头,我写了参考的文章,在那篇文章中,在文章结尾作者说java的array中的sort方法使用的TimSort就是一种优化版本的归并排序,我之前正好看过这个方法,当时并不知道什么是归并排序,当时看到sort排序的时候感觉作者Tim Peter真牛逼,这也可以想到,现在看来,其实他就是在归并排序的基础上做了点优化而已。具体优化的地方就是如下几点:
1.他没有把数组拆分成一个一个的元素,而拆成最小的单元为32,如果拆分的片段的长度小于32,采用的是二分插入排序,如果不了解这个算法的,可以参考我另一篇文章:插入排序
2.寻找自然升序或者降序片段,防止出现了逆序的,然后再使用插入排序效率很低
3.在合并两个片段的时候会互相寻找合适的起始点和结束点
(。。。)
并没有列举完,里面还有几个优化的点,不好用文字叙述出来,反正在我看来,只要能优化的点,Tim Peter都捣鼓了一下
具体参考我的另一篇文章:java8中List中sort方法解析



