ROC曲线
ROC曲线指受试者工作特征曲线 / 接收器操作特性曲线(receiver operating characteristic curve), 是反映敏感性和特异性连续变量的综合指标,是用构图法揭示敏感性和特异性的相互关系，它通过将连续变量设定出多个不同的临界值，从而计算出一系列敏感性和特异性，再以敏感性为纵坐标、（1-特异性）为横坐标绘制成曲线，曲线下面积越大，诊断准确性越高。在ROC曲线上，最靠近坐标图左上方的点为敏感性和特异性均较高的临界值。
ROC曲线的例子
考虑一个二分问题，即将实例分成正类（positive）或负类（negative）。对一个二分问题来说，会出现四种情况。如果一个实例是正类并且也被 预测成正类，即为真正类（True positive）,如果实例是负类被预测成正类，称之为假正类（False positive）。相应地，如果实例是负类被预测成负类，称之为真负类（True negative）,正类被预测成负类则为假负类（false negative）。
TP：正确肯定的数目；
FN：漏报，没有正确找到的匹配的数目；
FP：误报，给出的匹配是不正确的；
TN：正确拒绝的非匹配对数；
列联表如下表所示，1代表正类，0代表负类。
| 预测 | ||||
| 1 | 0 | 合计 | ||
| 实际 | 1 | True Positive（TP） | False Negative（FN） | Actual Positive(TP+FN) |
| 0 | False Positive（FP) | True Negative(TN) | Actual Negative(FP+TN) | |
| 合计 | Predicted Positive(TP+FP) | Predicted Negative(FN+TN) | TP+FP+FN+TN |
从列联表引入两个新名词。其一是真正类率(true positive rate ,TPR), 计算公式为TPR=TP/ (TP+ FN)，刻画的是分类器所识别出的 正实例占所有正实例的比例。另外一个是负正类率(false positive rate, FPR),计算公式为FPR= FP / (FP + TN)，计算的是分类器错认为正类的负实例占所有负实例的比例。还有一个真负类率（True Negative Rate，TNR），也称为specificity,计算公式为TNR=TN/ (FP+ TN) = 1-FPR。
其中，两列True matches和True non-match分别代表应该匹配上和不应该匹配上的
两行Pred matches和Pred non-match分别代表预测匹配上和预测不匹配上的
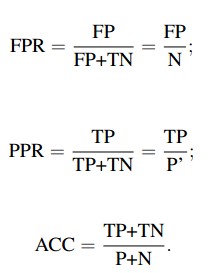PPR应该是TPR
|
预测
|
||||
|
1
|
0
|
合计
|
||
|
实际
|
1
|
True Positive（TP）
|
False Negative（FN）
|
Actual Positive(TP+FN)
|
|
0
|
False Positive（FP)
|
True Negative(TN)
|
Actual Negative(FP+TN)
|
|
|
合计
|
Predicted Positive(TP+FP)
|
Predicted Negative(FN+TN)
|
TP+FP+FN+TN
|
在一个二分类模型中，对于所得到的连续结果，假设已确定一个阀值，比如说 0.6，大于这个值的实例划归为正类，小于这个值则划到负类中。如果减小阀值，减到0.5，固然能识别出更多的正类，也就是提高了识别出的正例占所有正例 的比类，即TPR,但同时也将更多的负实例当作了正实例，即提高了FPR。为了形象化这一变化，在此引入ROC，ROC曲线可以用于评价一个分类器。
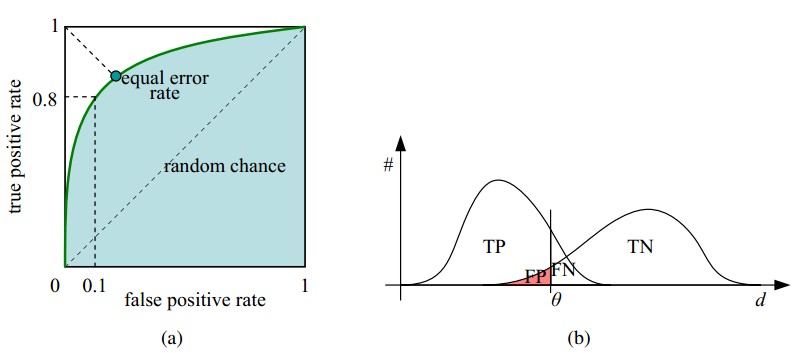
ROC曲线和它相关的比率
(a)理想情况下，TPR应该接近1，FPR应该接近0。
ROC曲线上的每一个点对应于一个threshold，对于一个分类器，每个threshold下会有一个TPR和FPR。
比如Threshold最大时，TP=FP=0，对应于原点；Threshold最小时，TN=FN=0，对应于右上角的点(1,1)
(b)P和N得分不作为特征间距离d的一个函数，随着阈值theta增加，TP和FP都增加
Receiver Operating Characteristic,翻译为"接受者操作特性曲线"，够拗口的。曲线由两个变量1-specificity 和 Sensitivity绘制. 1-specificity=FPR，即负正类率。Sensitivity即是真正类率，TPR(True positive rate),反映了正类覆盖程度。这个组合以1-specificity对sensitivity,即是以代价(costs)对收益(benefits)。
此外，ROC曲线还可以用来计算“均值平均精度”（mean average precision），这是当你通过改变阈值来选择最好的结果时所得到的平均精度（PPV）.
下表是一个逻辑回归得到的结果。将得到的实数值按大到小划分成10个个数 相同的部分。
| Percentile | 实例数 | 正例数 | 1-特异度(%) | 敏感度(%) |
| 10 | 6180 | 4879 | 2.73 | 34.64 |
| 20 | 6180 | 2804 | 9.80 | 54.55 |
| 30 | 6180 | 2165 | 18.22 | 69.92 |
| 40 | 6180 | 1506 | 28.01 | 80.62 |
| 50 | 6180 | 987 | 38.90 | 87.62 |
| 60 | 6180 | 529 | 50.74 | 91.38 |
| 70 | 6180 | 365 | 62.93 | 93.97 |
| 80 | 6180 | 294 | 75.26 | 96.06 |
| 90 | 6180 | 297 | 87.59 | 98.17 |
| 100 | 6177 | 258 | 100.00 | 100.00 |
其正例数为此部分里实际的正类数。也就是说，将逻辑回归得到的结 果按从大到小排列，倘若以前10%的数值作为阀值，即将前10%的实例都划归为正类，6180个。其中，正确的个数为4879个，占所有正类的 4879/14084*100%=34.64%，即敏感度；另外，有6180-4879=1301个负实例被错划为正类，占所有负类的1301 /47713*100%=2.73%,即1-特异度。以这两组值分别作为x值和y值，在excel中作散点图。
