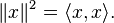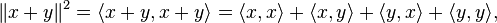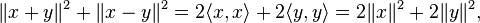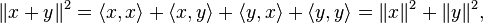parallelogram

The parallelogram law in inner product spaces

Vectors involved in the parallelogram law.

In a normed space, the statement of the parallelogram law is an equation relating norms:

2\|x\|^2+2\|y\|^2=\|x+y\|^2+\|x-y\|^2. \,

In an inner product space, the norm is determined using the inner product:

\|x\|^2=\langle x, x\rangle.\,

As a consequence of this definition, in an inner product space the parallelogram law is an algebraic identity, readily established using the properties of the inner product:

\|x+y\|^2=\langle x+y, x+y\rangle= \langle x, x\rangle + \langle x, y\rangle +\langle y, x\rangle +\langle y, y\rangle, \,
\|x-y\|^2 =\langle x-y, x-y\rangle= \langle x, x\rangle - \langle x, y\rangle -\langle y, x\rangle +\langle y, y\rangle. \,

Adding these two expressions:

\|x+y\|^2+\|x-y\|^2 = 2\langle x, x\rangle + 2\langle y, y\rangle = 2\|x\|^2+2\|y\|^2, \,

as required.

If x is orthogonal to y, then 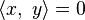\langle x ,\ y\rangle = 0 and the above equation for the norm of a sum becomes:

\|x+y\|^2= \langle x, x\rangle + \langle x, y\rangle +\langle y, x\rangle +\langle y, y\rangle =\|x\|^2+\|y\|^2,

which is Pythagoras' theorem.

posted @ 2014-10-18 09:59  代码学习者coding  阅读(566)  评论(0)  编辑  收藏  举报