Booth算法-乘法器设计
参考博文:https://blog.csdn.net/weixin_33847182/article/details/85779067 和 https://www.cnblogs.com/wangkai2019/p/11144367.html
乘法器——booth算法设计过程1

可以证明的是,这三个公式是相等的,一个有符号的二进制数的补码用公式1来表示,可以等价地写成公式2和公式3。
布斯编码可以减少部分积的数目(即减少乘数中1的个数),用来计算有符号乘法,提高乘法运算的速度。
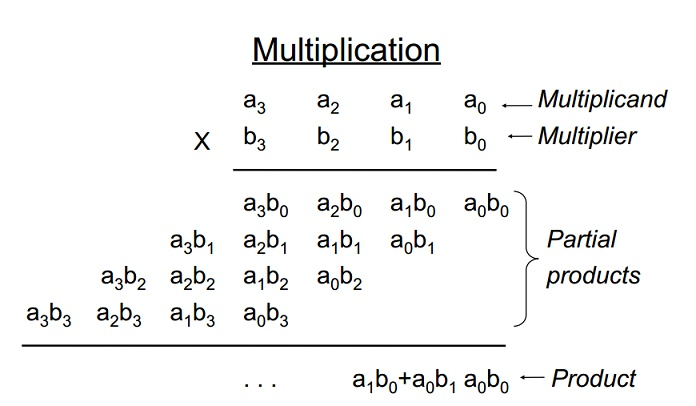
如上图所示为二进制乘法的过程,也是符合我们正常计算时的逻辑,我们假设有一个8位乘数(Multiplier),它的二进制值为0111_1110,它将产生6行非零的部分积,因为它有6个非零值(即1)。如果我们利用公式2将这个二进制值改为1000_00-10,其中低四位中的-1表示负1,可以证明两个值是相等的。可以这样简单理解,那就是现在原值得末尾加辅助位0,变为0111_1110_0,然后利用低位减去高位,即得到1000_00-10。这样一变换可以减少0的数目,从而减少加的次数,我们只需相加两个部分积,但是终的加法器必须也能执行减法。这种形式的变换称为booth encoding(即booth编码),它保证了在每两个连续位中最多只有一个是1或-1。部分积数目的减少意味着相加次数的减少,从而加快了运算速度(并减少了面积)。从形式上来说,这一变换相当于把乘数变换成一个四进制形式。
最经常使用的是改进的booth编码。乘数按三位一组进行划分,相互重叠一位。其实就是把公式1重写为公式3。每一组按下表编码,并形成一个部分积。

乘法器——booth算法设计过程2
这里讲解一下BOOTH算法的计算过程,方便大家对BOOTH的理解。
 上图是BOOTH算法的数学表达。由于FPGA擅长进行并行移位计算,所以BOOTH算法倒也好实现。
上图是BOOTH算法的数学表达。由于FPGA擅长进行并行移位计算,所以BOOTH算法倒也好实现。

上图是对乘数的加码过程,具体可以见下面的例子。
7 x (-3),其中R1表示被乘数 7, R2 表示乘数 -3,那么二者对应的补码,为 R1 0111,R2 1101,
P代码最终结果容量,应该为 2x 4 + 1 = 9位,其中一位作为辅助位。计算过程如下:
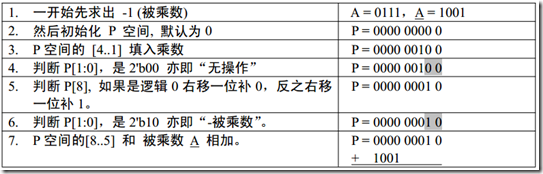
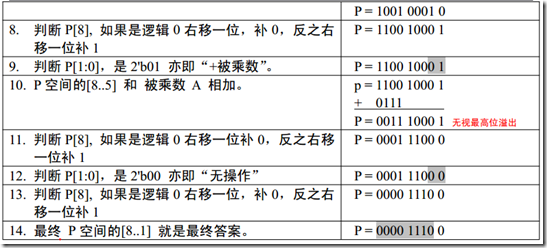
上述的计算过程需要注意,在进行右移时,需要将P = {R0,R2},当作整体看待,若P[8]最高位为0,则
移位之后的结果R0的最高位就补0,若是1就补1,由上图的第7步到第8步的变换,{R0,R2} =
{1001,,0001},那么P的最高位是1,则以后之后,R0的高位需要补1,所以得到移位之后的结果{R0,R2} =
{1100,1000},并且辅助位由于乘数的低位是1,所以辅助位为1,辅助位和乘数的移调的位的逻辑值有关,比
如乘数是0010,则四次操作的辅助为 0, 1, 0, 0。



