Separable/Group Convolution与Depthwise Convolution和Global Depthwise Convolution

参考博文：https://yinguobing.com/separable-convolution/#fn2和https://www.cnblogs.com/shine-lee/p/10243114.html

移动端设备的硬件性能限制了神经网络的规模。本文尝试解释一种被称为Separable Convolution的卷积运算方式。它将传统卷积分解为Depthwise Convolution与Pointwise Convolution两部分，有效的减小了参数数量。

卷积神经网络在图像处理中的地位已然毋庸置疑。卷积运算具备强大的特征提取能力、相比全连接又消耗更少的参数，应用在图像这样的二维结构数据中有着先天优势。然而受限于目前移动端设备硬件条件，显著降低神经网络的运算量依旧是网络结构优化的目标之一。本文所述的Separable Convolution就是降低卷积运算参数量的一种典型方法。

常规卷积运算

假设输入层为一个大小为64×64像素、三通道彩色图片。经过一个包含4个Filter的卷积层，最终输出4个Feature Map，且尺寸与输入层相同。整个过程可以用下图来概括。

 

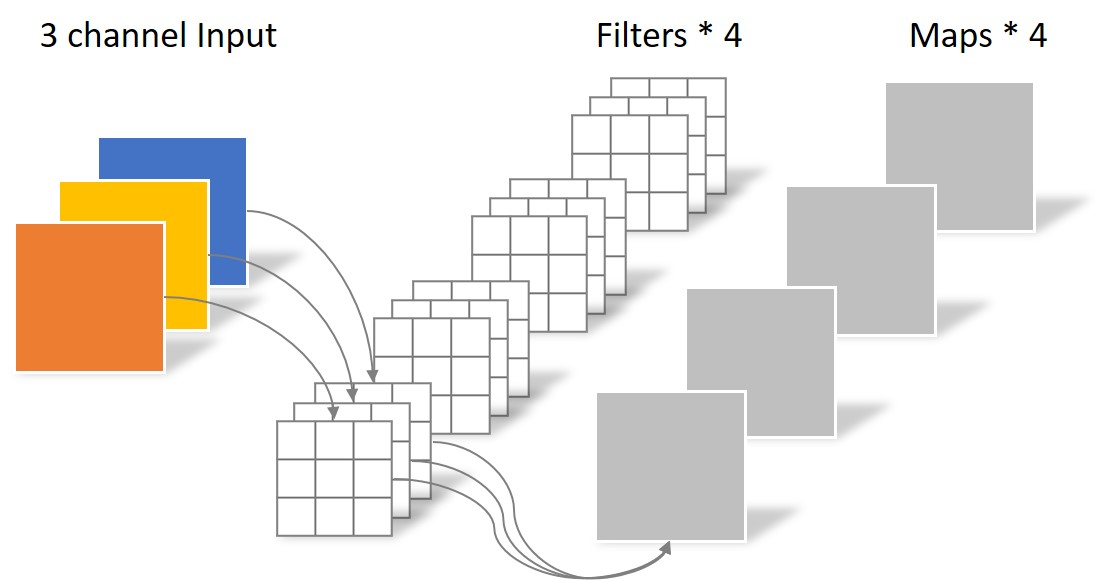
 此时，卷积层共4个Filter，每个Filter包含了3个Kernel，每个Kernel的大小为3×3。因此卷积层的参数数量可以用如下公式来计算：

N_std = 4 × 3 × 3 × 3 = 108

Separable Convolution

Separable Convolution在Google的Xception[1]以及MobileNet[2]论文中均有描述。它的核心思想是将一个完整的卷积运算分解为两步进行，分别为Depthwise Convolution与Pointwise Convolution。

Depthwise Convolution

同样是上述例子，一个大小为64×64像素、三通道彩色图片首先经过第一次卷积运算，不同之处在于此次的卷积完全是在二维平面内进行，且Filter的数量与上一层的Depth相同。所以一个三通道的图像经过运算后生成了3个Feature map，如下图所示。

 

 

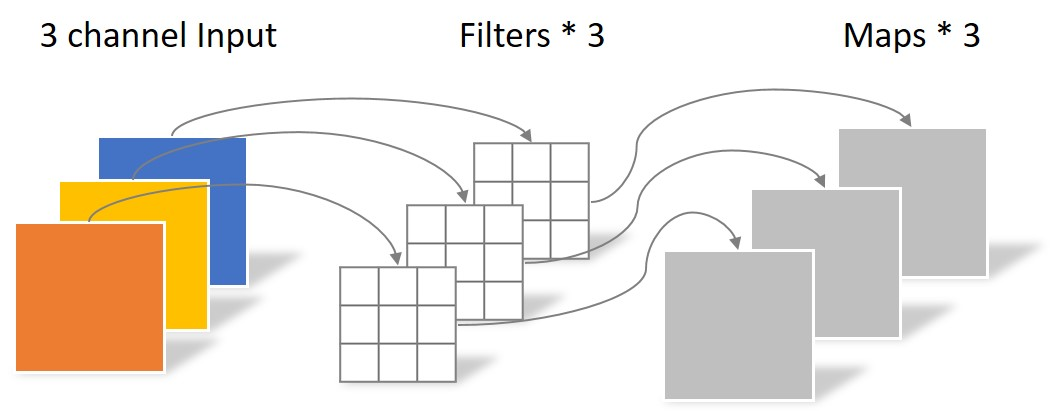
其中一个Filter只包含一个大小为3×3的Kernel，卷积部分的参数个数计算如下：

N_depthwise = 3 × 3 × 3 = 27

Depthwise Convolution完成后的Feature map数量与输入层的depth相同，但是这种运算对输入层的每个channel独立进行卷积运算后就结束了，没有有效的利用不同map在相同空间位置上的信息。因此需要增加另外一步操作来将这些map进行组合生成新的Feature map，即接下来的Pointwise Convolution。

Pointwise Convolution

Pointwise Convolution的运算与常规卷积运算非常相似，不同之处在于卷积核的尺寸为 1×1×M，M为上一层的depth。所以这里的卷积运算会将上一步的map在深度方向上进行加权组合，生成新的Feature map。有几个Filter就有几个Feature map。如下图所示。

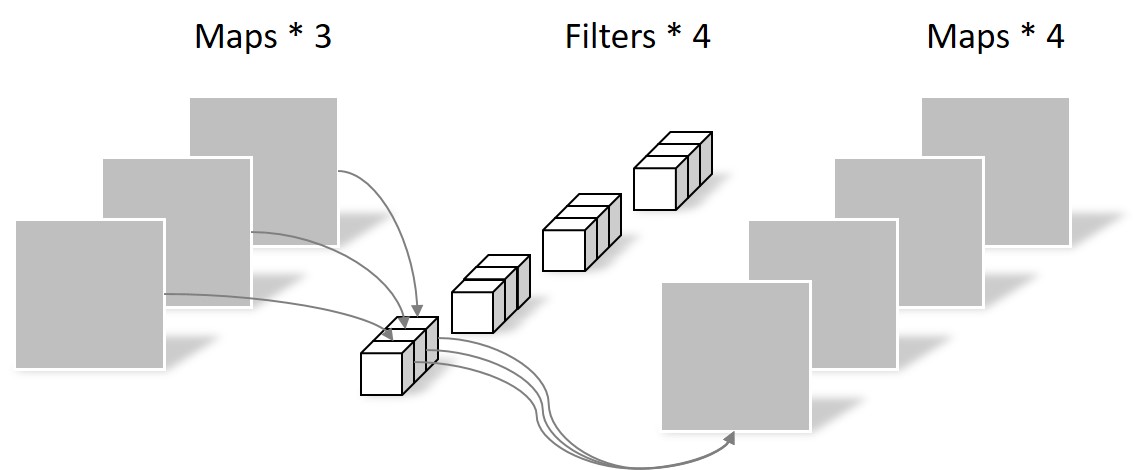
由于采用的是1×1卷积的方式，此步中卷积涉及到的参数个数可以计算为：

N_pointwise = 1 × 1 × 3 × 4 = 12

经过Pointwise Convolution之后，同样输出了4张Feature map，与常规卷积的输出维度相同。

参数对比

回顾一下，常规卷积的参数个数为：

N_std = 4 × 3 × 3 × 3 = 108

Separable Convolution的参数由两部分相加得到：

N_depthwise = 3 × 3 × 3 = 27
N_pointwise = 1 × 1 × 3 × 4 = 12
N_separable = N_depthwise + N_pointwise = 39

相同的输入，同样是得到4张Feature map，Separable Convolution的参数个数是常规卷积的约1/3。因此，在参数量相同的前提下，采用Separable Convolution的神经网络层数可以做的更深。

Group Convolution的用途

1. 减少参数量，分成GG组，则该层的参数量减少为原来的1G1G
2. Group Convolution可以看成是structured sparse，每个卷积核的尺寸由C∗K∗KC∗K∗K变为CG∗K∗KCG∗K∗K，可以将其余(C−CG)∗K∗K(C−CG)∗K∗K的参数视为0，有时甚至可以在减少参数量的同时获得更好的效果（相当于正则）。
3. 当分组数量等于输入map数量，输出map数量也等于输入map数量，即G=N=CG=N=C、NN个卷积核每个尺寸为1∗K∗K1∗K∗K时，Group Convolution就成了Depthwise Convolution，参见MobileNet和Xception等，参数量进一步缩减，如下图所示
   
4. 更进一步，如果分组数G=N=CG=N=C，同时卷积核的尺寸与输入map的尺寸相同，即K=H=WK=H=W，则输出map为C∗1∗1C∗1∗1即长度为CC的向量，此时称之为Global Depthwise Convolution（GDC），见MobileFaceNet，可以看成是全局加权池化，与 Global Average Pooling（GAP） 的不同之处在于，GDC 给每个位置赋予了可学习的权重（对于已对齐的图像这很有效，比如人脸，中心位置和边界位置的权重自然应该不同），而GAP每个位置的权重相同，全局取个平均，如下图所示：