Cache缓存淘汰算法
参考博文:https://www.cnblogs.com/dj0325/p/8846406.html 和 https://blog.csdn.net/zgcjaxj/article/details/104740111和
现代计算机体系结构中,cache一般采用组相连的形式。Cache替换算法是影响缓存系统性能的一个重要因素,一个好的Cache替换算法会适应各种不同的应用场景,产生较高的命中率。在采用全相联映射和组相联映射方式时,从主存向 Cache 传送一个新块,当 Cache 中的空间被占满时,就需要使用替换算法置换 Cache行。而采用直接映射则不需要考虑替换算法。常见的cache替换算法有以下几种。
随机算法(RAND) :随机地确定替换的Cache块。它的实现比较简单,但没有依据程序访问的局部性原理,故可能命中率较低。命中不做处理,未命中随机替换。
先进先出算法(FIFO) :选择最早调入的行进行替换。它比较容易实现,但也没有依据程序访问的局部性原理,可能会把一些需要经常使用的程序块(如循环程序)也作为最早进入Cache的块替换掉。命中不做处理,未命中替换最先进入的,会出现抖动现象。
近期最少使用算法(LRU):依据程序访问的局部性原理选择近期内长久未访问过的存储行作为替换的行,平均命中率要比FIFO要高,是堆栈类算法。LRU算法对每行设置一个计数器,Cache每命中一次,命中行计数器清0,而其他各行计数器均加1,需要替换时比较各特定行的计数值,将计数值最大的行换出。
最不经常使用算法(LFU):将一段时间内被访问次数最少的存储行换出。每行也设置一个计数器,新行建立后从0开始计数,每访问一次,被访问的行计数器加1,需要替换时比较各特定行的计数值,将计数值最小的行换出。
0, 可综合伪随机生成算法
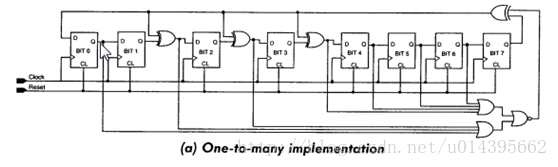
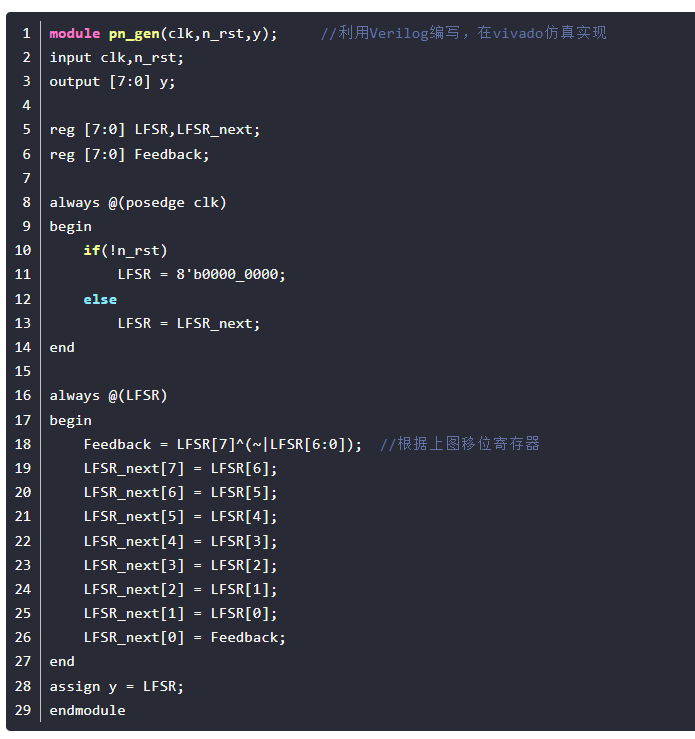
1,LRU
LRU ( Least Recently Used),即最近最少使用,是一种常用的cache替换算法,当没有free way时,选择最近最久未使用的way予以替换。来一个新的request后,基本处理流程如Figure 1。
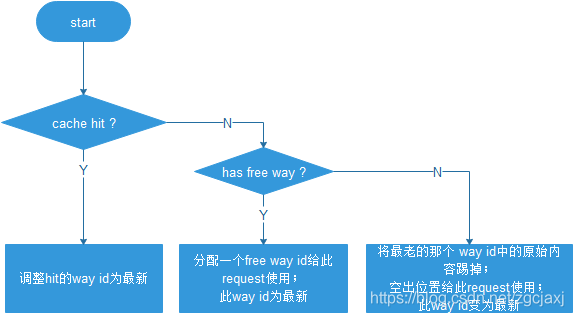
Figure 1 LRU流程图
举例来说,way num为4,set index为Addr[11:6],tag index为Addr[37:12]。request addr顺序依次为0x100040, 0x200040, 0x300040, 0x400040, 0x500040,则0x500040来的时候没有free way,需要踢掉一个way,踢掉0x100040。request addr顺序依次为0x100040, 0x200040, 0x300040, 0x400040, 0x100040, 0x500040,则0x500040来的时候没有free way,需要踢掉一个way,踢掉0x200040。因为0x100040 第2次来的时候hit cache,更新0x100040为最新,0x200040就变成最老的way了。
2,MRU
MRU (Mostly recently used),即最近最多使用,跟LRU是相反的一种替换算法,当没有free way时,选择最近最新未使用的way予以替换。
3, LRU & MRU的实现
对于LRU和MRU策略的实现,在一个set中,都需要维护一个表,表的长度等于way num,记录的内容是way id。如Figure 2,假设way num =4,pos_0是LRU position,pos_3是MRU position。

Figure 2 LRU、MRU实现方法示意图
如果采用LRU替换策略,新来的request分配way id后,此id 填在靠近MRU的位置;需要进行替换时,总是将pos_0对应的way原内容剔除,剔除后pos_0 id 转移到MRU位置,也就是变成pos_3,原来的pos_3 / pos_2/ pos_1 向右移动分别变为pos_2 / 1 / 0。如果发生cache hit,则将hit的way id 移到靠近MRU的位置,原位置上的id依次右移。
举例说明,way num为4,set index为Addr[11:6],tag index为Addr[37:12]。如果request addr顺序依次为0x000040, 0x100040, 0x200040, 0x000040,分配way id为0,1,2。则第2次0x000040时,LRU way id变化如Figure 3,pos_0的way id 转移到靠近MRU位置pos_2.
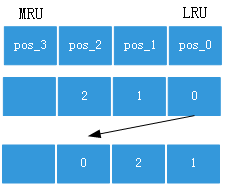
Figure 3 LRU 实例1
如果request addr顺序依次为0x100040, 0x200040, 0x300040, 0x400040, 0x100040, 0x500040,前四个分配way id依次为0,1,2,3. 第2次0x100040时,pos_0的way id 转移到MRU位置,也就是pos_3,原来的pos_3 / pos_2/ pos_1 向右移动。0x500040时,cache miss & no free way,将pos_0对应的way id (way 1)原始内容剔除,新request进入way 1。对于way id表格,pos_0 shift to MRU,其他向右移动。如Figure 4所示。

Figure 4 LRU实例2
如果采用MRU替换策略,新来的request分配way id后,此id 填在靠近LRU的位置;需要进行替换时,也总是将pos_0对应的way原内容剔除,但是pos_0 id 依然保持在 pos_0位置;下次再替换的时候,还是踢这个id。如果发生cache hit,则将hit的way id 移到靠近LRU的位置,原位置上的id依次左移。
举例说明。如果request addr顺序依次为0x100040, 0x200040, 0x300040, 0x400040, 0x100040, 0x500040,前四个分配way id依次为0,1,2,3. 第2次0x100040时,pos_3的way id 转移到LRU位置,也就是pos_0,原来的pos_3 / pos_2/ pos_1 向左移动。0x500040时,cache miss & no free way,将pos_0对应的way id (way 0)原始内容剔除,而way id表格保持不变。如Figure 5。

Figure 5 MRU实例1
4, Pseudo LRU
Pseudo LRU称之为伪LRU,也是一种常用的替换算法。以下,以way num = 16进行说明其实现方法。
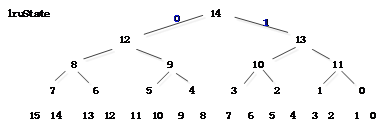
Figure 6 Pseudo LRU示意图
如图由15bit的 lruState[14:0]来表示一个二叉树的状态,二叉树的最后一行分别对应way id 0-15.
假设lruState[14:0]初始状态全部为1,选择way 0,之后lruState 14/13/11/0 翻转变为0。PLRU算法每次replace一个way id后,对应的lruState都要进行翻转。Replace时候根据二叉树的lruState的值进行选择way id。根据lruState的值,1 选右,0 选左。如果Hit某一way,路上经过的lruState不是翻转,而是尽量的避开指向我,即都导向另外一边。比如hit way 0, 那么state[0]指向1 ,state[11] 指向 2-3 , state[13] 指向 4-7, state[14] 指向 8-15。不管有没有free way,选择一个way id时都是根据lruState[14] 的状态,然后一路找下去, 选择之后路上的所有节点都要进行翻转。总之,set每次收到一个request,都会更新LruState,Hit cache时,避开指向hit的way id;否则对LruState进行翻转。
5,BIP
Bimodal Insertion Policy(BIP)替换策略,是LRU和MRU的结合体,大概率采用MRU替换,小概率采用LRU策略。
设置一个固定的max_miss,用于控制采用LRU的概率,其概率为1/max_miss。具体实现时,用一个counter来记录miss的次数,当miss counter == max_miss时采用LRU替换策略,发生替换时将pos_0 way id 移动到MRU位置,同时讲miss counter清零。当miss counter 不等于 max_miss时采用MRU替换策略,发生替换时保持pos_0 way id不变。
6,DIP
Dynamic Insertion Policy (DIP)替换策略,是以LRU和BIP替换策略为基础,在整个cache块中实施的一种方法。LRU、MRU、Pseudo LRU和BIP策略都是对每一个set来讲的,各个set间没有联系。而DIP策略可以认为是,根据某些set (LRU-set 和BIP-set)的采样情况来动态决定其他follower set的替换策略。
假设某1M 的cache,有1024个set,每个set有16个way。分别选择其中16个set作为LRU-set 和BIP-set,其他set为follower set。Set index 为A [15:6],Set的选择可以这样:A[15:11] == A [10:6] 设置为LRU-set;A[15:11] + id== A [10:6] 设置为BIP-set,这个id比如可以设置为2。用一个Policy Select Counter (PSEL_cnt)来记录LRU-set 和BIP-set的miss情况。其中,当LRU-set发生一次miss时,PSEL_cnt 加1;当BIP-set发生一次miss时,PSEL_cnt 减1。当PSEL_cnt 比较大时,表明当前执行的程序,使得采用LRU策略会发生的miss量超过了BIP策略,那就是应该让follower set采用BIP。但由于程序执行时对cache的冲击可能会有一定的波动性,故需要设定一个阈值(PSEL threshold),当PSEL_cnt大于等于这个阈值时,再让follower set 采用BIP;小于阈值时,依然采用LRU。PSEL_cnt 在超过PSEL threshold时,如果再发生LRU-set miss也不再进行加1操作,也就是说PSEL_cnt的取值范围为[ 0 , PSEL threshold ]。
一般的介绍资料中会提到,当PSEL_cnt的MSB (Most Significant Bit,最高有效位)为1时,选择BIP,否则选择LRU。在RTL实现时,比如准备设置PSEL threshold = 1024,则PSEL cnt就需要11 bit,当PSEL_cnt的MSB为1时,就是PSEL_cnt = PSEL threshold。如Figure 7、Figure 8和Figure 9为DIP策略的具体实现流程图,其中Figure 7为主流程图,主要为pos更新和替换的流程,Figure 8为miss cnt的更新,Figure 9为PSEL cnt的更新流程。
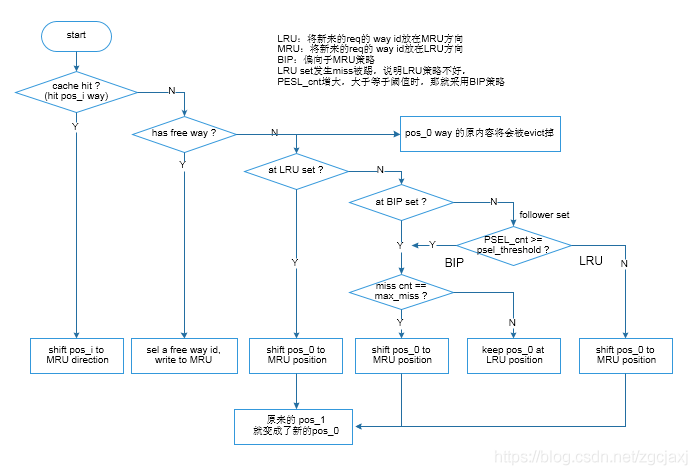
Figure 7 DIP流程图1 (替换策略)
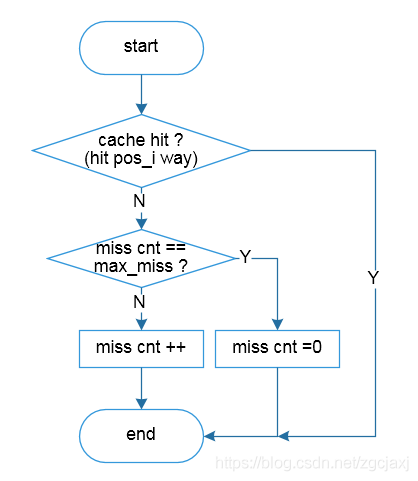
Figure 8 DIP流程图2 (miss cnt更新)
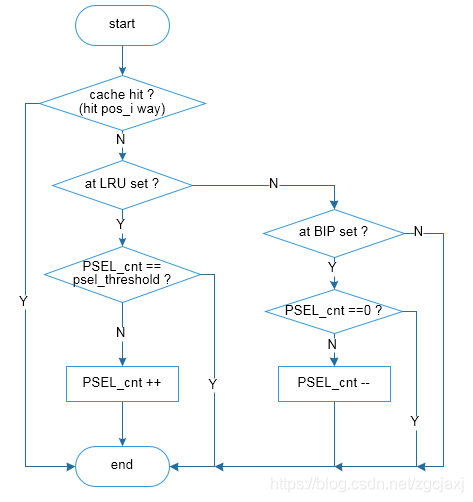
Figure 9 DIP流程图3 (PSEL cnt 更新)
在DIP的基础上,还有更进一步的策略,如Thread Aware DIP-Isolation (TADIP-I) and TADIP-Feedback (TADIP-F).
LRU详细过程
1.1. 原理
LRU(Least recently used,最近最少使用)算法根据数据的历史访问记录来进行淘汰数据,其核心思想是“如果数据最近被访问过,那么将来被访问的几率也更高”。
1.2. 实现
最常见的实现是使用一个链表保存缓存数据,详细算法实现如下:
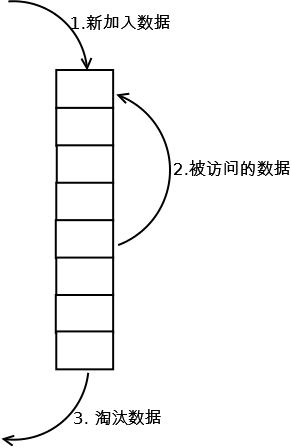
1. 新数据插入到链表头部;
2. 每当缓存命中(即缓存数据被访问),则将数据移到链表头部;
3. 当链表满的时候,将链表尾部的数据丢弃。
1.3. 分析
【命中率】
当存在热点数据时,LRU的效率很好,但偶发性的、周期性的批量操作会导致LRU命中率急剧下降,缓存污染情况比较严重。
【复杂度】
实现简单。
【代价】
命中时需要遍历链表,找到命中的数据块索引,然后需要将数据移到头部。
LRU-K
2.1. 原理
LRU-K中的K代表最近使用的次数,因此LRU可以认为是LRU-1。LRU-K的主要目的是为了解决LRU算法“缓存污染”的问题,其核心思想是将“最近使用过1次”的判断标准扩展为“最近使用过K次”。
2.2. 实现
相比LRU,LRU-K需要多维护一个队列,用于记录所有缓存数据被访问的历史。只有当数据的访问次数达到K次的时候,才将数据放入缓存。当需要淘汰数据时,LRU-K会淘汰第K次访问时间距当前时间最大的数据。详细实现如下:
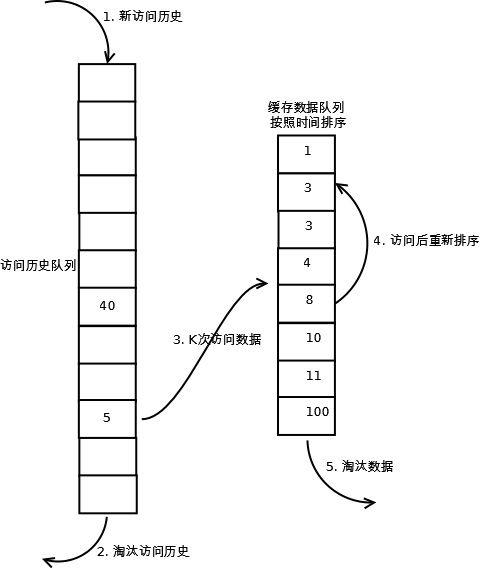
1. 数据第一次被访问,加入到访问历史列表;
2. 如果数据在访问历史列表里后没有达到K次访问,则按照一定规则(FIFO,LRU)淘汰;
3. 当访问历史队列中的数据访问次数达到K次后,将数据索引从历史队列删除,将数据移到缓存队列中,并缓存此数据,缓存队列重新按照时间排序;
4. 缓存数据队列中被再次访问后,重新排序;
5. 需要淘汰数据时,淘汰缓存队列中排在末尾的数据,即:淘汰“倒数第K次访问离现在最久”的数据。
LRU-K具有LRU的优点,同时能够避免LRU的缺点,实际应用中LRU-2是综合各种因素后最优的选择,LRU-3或者更大的K值命中率会高,但适应性差,需要大量的数据访问才能将历史访问记录清除掉。
2.3. 分析
【命中率】
LRU-K降低了“缓存污染”带来的问题,命中率比LRU要高。
【复杂度】
LRU-K队列是一个优先级队列,算法复杂度和代价比较高。
【代价】
由于LRU-K还需要记录那些被访问过、但还没有放入缓存的对象,因此内存消耗会比LRU要多;当数据量很大的时候,内存消耗会比较可观。
LRU-K需要基于时间进行排序(可以需要淘汰时再排序,也可以即时排序),CPU消耗比LRU要高。
Two queues(2Q)
3.1. 原理
Two queues(以下使用2Q代替)算法类似于LRU-2,不同点在于2Q将LRU-2算法中的访问历史队列(注意这不是缓存数据的)改为一个FIFO缓存队列,即:2Q算法有两个缓存队列,一个是FIFO队列,一个是LRU队列。
3.2. 实现
当数据第一次访问时,2Q算法将数据缓存在FIFO队列里面,当数据第二次被访问时,则将数据从FIFO队列移到LRU队列里面,两个队列各自按照自己的方法淘汰数据。详细实现如下:
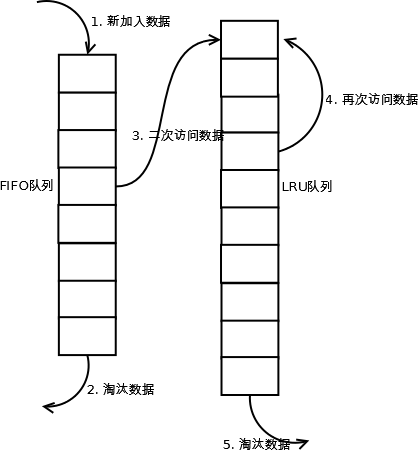
1. 新访问的数据插入到FIFO队列;
2. 如果数据在FIFO队列中一直没有被再次访问,则最终按照FIFO规则淘汰;
3. 如果数据在FIFO队列中被再次访问,则将数据移到LRU队列头部;
4. 如果数据在LRU队列再次被访问,则将数据移到LRU队列头部;
5. LRU队列淘汰末尾的数据。
注:上图中FIFO队列比LRU队列短,但并不代表这是算法要求,实际应用中两者比例没有硬性规定。
3.3. 分析
【命中率】
2Q算法的命中率要高于LRU。
【复杂度】
需要两个队列,但两个队列本身都比较简单。
【代价】
FIFO和LRU的代价之和。
2Q算法和LRU-2算法命中率类似,内存消耗也比较接近,但对于最后缓存的数据来说,2Q会减少一次从原始存储读取数据或者计算数据的操作。
Multi Queue(MQ)
4.1. 原理
MQ算法根据访问频率将数据划分为多个队列,不同的队列具有不同的访问优先级,其核心思想是:优先缓存访问次数多的数据。
4.2. 实现
MQ算法将缓存划分为多个LRU队列,每个队列对应不同的访问优先级。访问优先级是根据访问次数计算出来的,例如
详细的算法结构图如下,Q0,Q1....Qk代表不同的优先级队列,Q-history代表从缓存中淘汰数据,但记录了数据的索引和引用次数的队列:
如上图,算法详细描述如下:
1. 新插入的数据放入Q0;
2. 每个队列按照LRU管理数据;
3. 当数据的访问次数达到一定次数,需要提升优先级时,将数据从当前队列删除,加入到高一级队列的头部;
4. 为了防止高优先级数据永远不被淘汰,当数据在指定的时间里访问没有被访问时,需要降低优先级,将数据从当前队列删除,加入到低一级的队列头部;
5. 需要淘汰数据时,从最低一级队列开始按照LRU淘汰;每个队列淘汰数据时,将数据从缓存中删除,将数据索引加入Q-history头部;
6. 如果数据在Q-history中被重新访问,则重新计算其优先级,移到目标队列的头部;
7. Q-history按照LRU淘汰数据的索引。
4.3. 分析
【命中率】
MQ降低了“缓存污染”带来的问题,命中率比LRU要高。
【复杂度】
MQ需要维护多个队列,且需要维护每个数据的访问时间,复杂度比LRU高。
【代价】
MQ需要记录每个数据的访问时间,需要定时扫描所有队列,代价比LRU要高。
注:虽然MQ的队列看起来数量比较多,但由于所有队列之和受限于缓存容量的大小,因此这里多个队列长度之和和一个LRU队列是一样的,因此队列扫描性能也相近。
LRU类算法对比
由于不同的访问模型导致命中率变化较大,此处对比仅基于理论定性分析,不做定量分析。
|
对比点 |
对比 |
|
命中率 |
LRU-2 > MQ(2) > 2Q > LRU |
|
复杂度 |
LRU-2 > MQ(2) > 2Q > LRU |
|
代价 |
LRU-2 > MQ(2) > 2Q > LRU |
实际应用中需要根据业务的需求和对数据的访问情况进行选择,并不是命中率越高越好。例如:虽然LRU看起来命中率会低一些,且存在”缓存污染“的问题,但由于其简单和代价小,实际应用中反而应用更多。




