极限limit

"极限"是数学中的分支——微积分的基础概念，本文简要讲解极限的基础知识，题型以及常用解法

$\\$

The Limit

两个重要极限

$$\displaystyle\lim_{x\to 0}\frac{sinx}{x}=1$$

$$\displaystyle\lim_{x\to \infty}(1+x)^{\frac{1}{x}}=e$$

性质

唯一性

如果极限存在，则该极限是唯一的。即：

$$\lim_{x \to c} f(x) = L \quad \text{如果且仅如果} \quad \forall \epsilon > 0, \exists \delta > 0, \text{使得当 } 0 < |x - c| < \delta \text{ 时 } |f(x) - L| < \epsilon$$

代数运算

如果极限存在，则可以对极限进行代数运算：

• 加减法：

$$\lim_{x \to c} [f(x) \pm g(x)] = \lim_{x \to c} f(x) \pm \lim_{x \to c} g(x)$$

• 乘法：

$$\lim_{x \to c} [f(x) \cdot g(x)] = \lim_{x \to c} f(x) \cdot \lim_{x \to c} g(x)$$

• 除法（前提是 ($\displaystyle\lim_{x \to c} g(x) \neq 0$)）：

$$\lim_{x \to c} \frac{f(x)}{g(x)} = \frac{\lim_{x \to c} f(x)}{\lim_{x \to c} g(x)}$$

连续性

可导一定连续，连续不一定导数

$y=f|x|$在$x=0$处不可导
由连续可知

$$\lim_{x\to c^-}f(x)=\lim_{x\to c^+}f(x)$$

$f(x)$在区间$[a,b]$连续，$f(x)_{min}<=f(x)<=f(x)_{max}$

保号性

定义：
设 $f(x)$ 是一个定义在某个区间上的函数，且在某点 $c$ 的邻域内，$f(x)$ 的值始终保持正（或负）。如果极限 $\lim _{x \to c} f(x)$ 存在，那么该极限的符号与 $f(x)$ 在 $c$ 附近的符号一致。
利用它可以判断正负

无穷小

定义：极限变量为0的点
比较：$f(x)$是$g(x)$的___无穷小
1.等价：$\displaystyle \lim_{x \to 0}\frac{f(x)}{g(x)}=1$
2.同阶：$\displaystyle \lim_{x \to 0}\frac{f(x)}{g(x)}=c(c\neq 1，0)$，c is a constant
3.高阶：$\displaystyle \lim_{x \to 0}\frac{f(x)}{g(x)}=0$

间断点

1.第一类间断点

第一类间断点是指在该点附近的函数值存在，但在该点的极限不存在。具体来说，若 $f(x)$ 在 $x = c$ 附近的左极限和右极限都存在，但不相等，即：

$$\lim_{x \to c^-} f(x) \neq \lim_{x \to c^+} f(x)$$

此时，函数在 $x = c$ 处的值可以是有限的或无穷大。
2.第二类间断点

第二类间断点则是指在该点的极限不存在，且至少有一个方向的极限也不存在。即:

$$\lim_{x \to c} f(x) 不存在$$

闭区间连续函数性质

• 最值定理：必有最值
• 有界定理：最有最小值和最大值
• 介值定理：设 ( $f(x)$ ) 是一个在闭区间 ($[a, b]$) 上连续的函数。如果 ( $f(a)$ ) 和 ( $f(b)$ ) 的值分别为 ( $f(a)$ ) 和 ( $f(b)$ )，且 ($f(a) \neq f(b)$ )，那么对于任意的 ( y ) 值，满足 ($f(a) < y < f(b)$ ) 或 ($f(b) < y < f(a)$ )，存在至少一个 ($c \in (a, b)$)，使得：

$$f(c) = y$$

• 零点定理：设 ($f(x)$ ) 是一个在闭区间 ($[a, b]$) 上连续的函数。如果 ($f(a)$) 和 ( $f(b)$ ) 的符号相反，即 ( $f(a) \cdot f(b) < 0$ )，那么在区间 ($(a, b)$) 内至少存在一个 ($c$) 使得：

$$f(c) = 0$$

题型与解法

一些小技巧

1. 利用四则运算，分开算极限
2. 分子或者分母有理化
3. 因式分解
4. 常见的函数的性质:奇偶性
5. 换元法：三角换元，取倒数

取倒数

对于一些$x\to \infty$的情况，我们可以令$t=\frac{1}{x}$
则$t\to 0$转为我们比较熟悉的极限求解
例如

$$\displaystyle\lim_{x\to\infty}xsin\frac{1}{x}=\lim_{x\to\infty}\frac{sin\frac{1}{x}}{\frac{1}{x}}=e$$

取指数

对于$\forall x>0 ,x=e^{\ln x}$，同理

$$\lim u(x)^{v(x)}=\lim e^{v(x)\ln u(x)}$$

通过这样的操作，将指数分出，在求极限时可以有更多的变化

泰勒展开

1. 等价无穷小

   等价无穷小其实就是泰勒展开的特殊情况
   
   在求极限使用时，只有式子的因子可以这样的用，如果直接当成加减法使用，答案会不正确，因为还有更小的没有考虑到

2. 泰勒展开

泰勒展开公式

指数函数 $e^{x}$：

• 展开式为 $e^{x}=\sum_{n = 0}^{\infty} \frac{1}{n!}x^{n}=1 + x+\frac{1}{2!}x^{2}+\cdots+\frac{1}{n!}x^{n}+\cdots$，$x\in(-\infty,+\infty)$。

正弦函数 $\sin x$：

• 展开式为 $\sin x=\sum_{n = 0}^{\infty} \frac{(-1)^{n}}{(2n + 1)!}x^{2n + 1}=x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{3}-\cdots+\frac{(-1)^{n}}{(2n + 1)!}x^{2n + 1}+\cdots$，$x\in(-\infty,+\infty)$。

余弦函数 $\cos x$：

• 展开式为 $\cos x=\sum_{n = 0}^{\infty} \frac{(-1)^{n}}{(2n)!}x^{2n}=1-\frac{1}{2!}x^{2}+\frac{1}{4!}x^{4}-\cdots+\frac{(-1)^{n}}{(2n)!}x^{2n}+\cdots$，$x\in(-\infty,+\infty)$。

自然对数函数 $\ln(1 + x)$：

• 展开式为 $\ln (1+x)=\sum_{n = 0}^{\infty} \frac{(-1)^{n}}{n + 1}x^{n + 1}=x-\frac{1}{2}x^{2}+\frac{1}{3}x^{3}-\cdots+\frac{(-1)^{n}}{n + 1}x^{n + 1}+\cdots$，$x\in(-1,1]$。

函数 $\frac{1}{1 - x}$：

• 展开式为 $\frac{1}{1 - x}=\sum_{n = 0}^{\infty}x^{n}=1 + x + x^{2}+x^{3}+\cdots+x^{n}+\cdots$，$x\in(-1,1)$。

函数 $\frac{1}{1 + x}$：

• 展开式为 $\frac{1}{1 + x}=\sum_{n = 0}^{\infty}(-1)^{n}x^{n}=1 - x + x^{2}-x^{3}+\cdots+(-1)^{n}x^{n}+\cdots$，$x\in(-1,1)$。

7. 函数 $(1 + x)^{\alpha}$：
   • 展开式为 $(1+x)^{\alpha}=1+\sum_{n = 1}^{\infty} \frac{\alpha(\alpha - 1)\cdots(\alpha - n + 1)}{n!}x^{n}=1+\alpha x+\frac{\alpha(\alpha - 1)}{2!}x^{2}+\cdots+\frac{\alpha(\alpha - 1)\cdots(\alpha - n + 1)}{n!}x^{n}+\cdots$，$x\in(-1,1)$。

反正切函数 $\arctan x$：

• 展开式为 $\arctan x=\sum_{n = 0}^{\infty} \frac{(-1)^{n}}{2n + 1}x^{2n + 1}=x-\frac{1}{3}x^{3}+\frac{1}{5}x^{5}+\cdots+\frac{(-1)^{n}}{2n + 1}x^{2n + 1}+\cdots$，$x\in[-1,1]$。

反正弦函数 $\arcsin x$：

• 展开式为 $\arcsin x=\sum_{n = 0}^{\infty} \frac{(2n)!}{4^{n}(n!)^{2}(2n + 1)}x^{2n + 1}=x+\frac{1}{6}x^{3}+\frac{3}{40}x^{3}+\frac{5}{112}x^{7}+\frac{35}{1152}x^{9}+\cdots+\frac{(2n)!}{4^{n}(n!)^{2}(2n + 1)}x^{2n + 1}+\cdots$，$x\in(-1,1)$。

正切函数 $\tan x$：

• 展开式为 $\tan x=\sum_{n = 1}^{\infty} \frac{B_{2n}(-4)^{n}(1 - 4^{n})}{(2n)!}x^{2n - 1}=x+\frac{1}{3}x^{3}+\frac{2}{15}x^{5}+\frac{17}{315}x^{7}+\frac{62}{2835}x^{9}+\frac{1382}{155925}x^{11}+\cdots$，$x\in(-1,1)$。

正割函数 $\sec x$：

• 展开式为 $\sec x=\sum_{n = 0}^{\infty} \frac{(-1)^{n}E_{2n}x^{2n}}{(2n)!}=1+\frac{1}{2}x^{2}+\frac{5}{24}x^{4}+\frac{61}{720}x^{6}+\cdots$，$x\in(-\frac{\pi}{2},\frac{\pi}{2})$。

余割函数 $\csc x$：

• 展开式为 $\csc x=\sum_{n = 0}^{\infty} \frac{(-1)^{n + 1}2(2^{2n - 1}-1)B_{2n}}{(2n)!}x^{2n - 4}=\frac{1}{x}+\frac{1}{6}x+\frac{7}{360}x^{3}+\frac{31}{15120}x^{3}+\frac{127}{604800}x^{7}+\frac{73}{3421440}x^{9}+\frac{1414477}{65383718400}x^{11}+\cdots$，$x\in(0,\pi)$。

余切函数 $\cot x$：

• 展开式为 $\cot x=\sum_{n = 0}^{\infty} \frac{(-1)^{n}2^{2n}B_{2n}}{(2n)!}x^{2n - 1}=\frac{1}{x}-\frac{1}{3}x-\frac{1}{45}x^{3}-\frac{2}{945}x^{5}-\cdots$，$x\in(0,\pi)$。

双曲正弦函数 $\sinh x$：

• 展开式为 $\sinh x=\sum_{n = 0}^{\infty} \frac{x^{2n + 1}}{(2n + 1)!}=x+\frac{x^{3}}{3!}+\frac{x^{5}}{5!}+\frac{x^{7}}{7!}+\cdots+\frac{x^{2n + 1}}{(2n + 1)!}+\cdots$，$x\in(-\infty,+\infty)$。

双曲余弦函数 $\cosh x$：

• 展开式为 $\cosh x=\sum_{n = 0}^{\infty} \frac{x^{2n}}{(2n)!}=1+\frac{x^{2}}{2!}+\frac{x^{4}}{4!}+\frac{x^{6}}{6!}+\cdots+\frac{x^{2n}}{(2n)!}+\cdots$，$x\in(-\infty,+\infty)$。

双曲正切函数 $\tanh x$：

• 展开式为 $\tanh x=\sum_{n = 1}^{\infty} \frac{2^{2n}(2^{2n}-1)B_{2n}x^{2n - 1}}{(2n)!}=x-\frac{1}{3}x^{3}+\frac{2}{15}x^{5}-\frac{17}{315}x^{7}+\frac{62}{2835}x^{9}-\frac{1382}{155925}x^{11}+\cdots$，$\vert x\vert\lt\frac{\pi}{2}$。

双曲正割函数 $\operatorname{sech} x$：

• 展开式为 $\operatorname{sech} x=\sum_{n = 0}^{\infty}\left(\frac{(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}\right)\frac{x^{2n + 1}}{(2n + 1)}=x-\frac{1}{6}x^{3}+\frac{3}{40}x^{5}-\frac{5}{112}x^{7}+\frac{35}{1152}x^{9}-\cdots+\left(\frac{(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}\right)\frac{x^{2n + 1}}{(2n + 1)}+\cdots$，$\vert x\vert\lt1$。

反双曲正弦函数 $\operatorname{arcsinh} x$：

• 展开式为 $\operatorname{arcsinh} x=\ln 2x-\left(\frac{(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}\right)\frac{x^{-2n}}{2n}=\ln 2x-\left(\frac{1}{4}x^{-2}+\frac{3}{32}x^{-4}+\frac{15}{288}x^{-6}+\cdots+\left(\frac{(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}\right)\frac{x^{-2n}}{2n}+\cdots\right)$，$\vert x\vert\gt1$。

反双曲正切函数 $\operatorname{arctanh} x$：

• 展开式为 $\operatorname{arctanh} x=\sum_{n = 0}^{\infty} \frac{x^{2n + 1}}{2n + 1}=x+\frac{x^{3}}{3}+\frac{x^{5}}{5}+\frac{x^{7}}{7}+\cdots+\frac{x^{2n + 1}}{2n + 1}+\cdots$，$\vert x\vert\lt1$。

例题： $$\displaystyle\lim_{x \to 0}\frac{x-sinx}{x^3}=\lim_{x\to 0}\frac{x-(x-x^3+o(x^3))}{x^3}=1$$

其实你可以发现，用泰勒展开就可以得到等价无穷小
泰勒展开的唯一要求就是在展开时，展开的最高此项与已有的相同

夹逼定理

大白话：夹逼定理就是通过左右放缩，使得趋于极限时，左右的值都接近，使得原式不得不与左右值相近

从某项起，即当$(n > N)$时，有$(y_n\leqslant x_n\leqslant z_n)$。

$$\lim\limits_{n\to\infty}y_n=\lim\limits_{n\to\infty}z_n = a$$

那么数列${x_n}$的极限存在，且$\lim\limits_{n\to\infty}x_n = a$

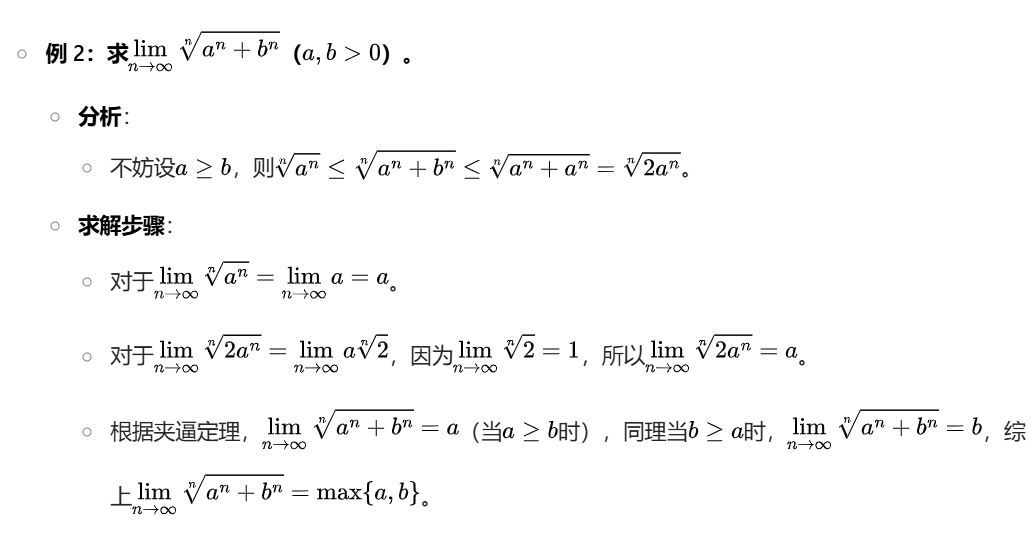
洛必达法则

使用时需注意$x=x_0$处的领域有定义

$$\lim_{x\to x_0}\frac{f(x)}{g(x)}=\lim_{x\to x_0}\frac{f'(x)}{g'(x)}=\lim_{x\to x_0}\frac{f''(x)}{g''(x)}=....=\lim_{x\to x_0}\frac{f^{(n)}(x)}{g^{(n)}(x)}$$

使用情况

1. 0/0 不定型

当计算极限时，如果得到的形式是 (\frac{0}{0})，则可以应用洛必达法则。此时，可以对分子和分母分别求导，然后再计算极限：

$$\lim_{x \to c} \frac{f(x)}{g(x)} = \lim_{x \to c} \frac{f'(x)}{g'(x)}$$

2. ∞/∞ 不定型

如果计算的极限形式是 \frac{\infty}{\infty}，也可以使用洛必达法则。方法同样是对分子和分母分别求导：

$$\lim_{x \to c} \frac{f(x)}{g(x)} = \lim_{x \to c} \frac{f'(x)}{g'(x)}$$

3. 0 · ∞ 不定型

对于形式为 $0 \cdot \infty$\ 的极限，可以通过将其转化为 (\frac{0}{0}) 或 (\frac{\infty}{\infty}) 的形式来应用洛必达法则。通常可以将其重写为：

$$\lim_{x \to c} f(x) \cdot g(x) = \lim_{x \to c} \frac{f(x)}{\frac{1}{g(x)}}$$

或

$$\lim_{x \to c} f(x) \cdot g(x) = \lim_{x \to c} \frac{g(x)}{\frac{1}{f(x)}}$$

4. ∞ - ∞ 不定型

对于形式为 $\infty - \infty$的极限，可以通过将其转化为分数的形式，例如：

$$\lim_{x \to c} (f(x) - g(x)) = \lim_{x \to c} \frac{f(x)g(x)}{g(x)} \text{ 或 } \frac{f(x) - g(x)}{1}$$

例题

$$\displaystyle\lim_{x\to 0}\frac{(\int_{0}^{x}e^tdt)^2}{\int_{0}^{x}e^{t^2}dt}=\lim_{x \to 0}\frac{2(\int_{0}^{x}e^tdt)}{e^{x^2-x}}=\lim_{x\to0}\frac{2e^x}{(2x-1)e^{x^2-x}}=-2$$

拉格朗日中值定理

使用条件:$f(x)$ 在 $（x_1,x_2）$可导

令$x_1<x_2$ 则 $\frac{f(x_2)-f(x_1)}{x_2-x_1}=f'(\epsilon), \epsilon \in(x_1,x_2)$

例题

$$\lim_{x\to 0^+}\frac{sinx-sin(sinx)}{x^3}=\lim_{x\to0^+}\frac{(sinx-x)f'(\epsilon)}{x^3}=\lim_{x\to 0^+}\frac{(sinx-x)cos\epsilon}{x^3} =\lim_{x\to0^+}\frac{(x-\frac{x^3}{3}+o(x^3)-x)cos\epsilon}{x^3}=-\frac{1}{3} \\ 由\epsilon \in (sinx,x) 则 lim_{x\to 0^+}\epsilon=0 \\ 即lim_{x\to 0^+}cos\epsilon=1 \\ $$