高精度计算
高精度
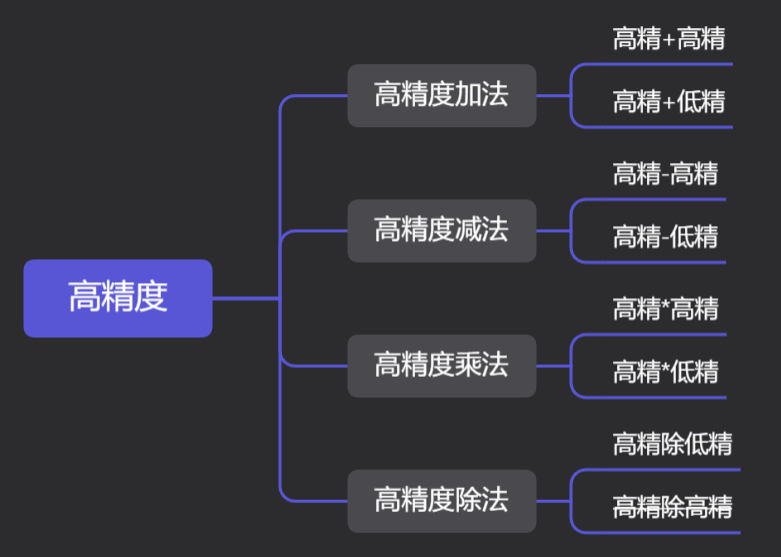
有四种高精度如下
(低精度意为可用long long 或int存储的数
高精度一般用于数无法用int,long long表示出来的时候使用
其本质都是用数组存数的每一位,模拟加减乘除,最后从高位输出到低位
(模拟竖式加减乘除)
高精度加法
一般从数组第一位存个位,第二位十位,第三位.....依次类推
(为什么数组第一位不为最高位,因为如果第一位是最高位遇到进位不好处理,会数组越界)
高精+高精
这部分内容不难,结合代码模拟下就懂了
#include<iostream>
#include<cstring>
using namespace std;
int n;const int maxn=1000;
int ans[maxn];
string s;
int len=0,lens;
int main(){
for(int i=1;i<=2;++i){
cin>>s;lens=s.length();len=lens>len?lens:len;
for(int j=lens-1;j>=0;--j) ans[lens-j-1]+=s[j]-'0';
}
for(int i=0;i<len;++i){
if(ans[i]>=10){
ans[i+1]+=ans[i]/10;
ans[i]%=10;
if(ans[len]>0) ++len; //最高位的下一位不为0,则数的长度++
}
}--len;
while(len>=0) cout<<ans[len],--len;
return 0;
}
高精+低精(
借鉴高精的做法,将低精转为数组,同样可行
高精度减法
高精度减法与加法不同的是,一个是进位,一个是借位(从后一个数借一个“1”)
注意会出现负数,判断一下大小,然后仍然用大数减小数
高精-高精
#include<cstdio>
#include<cstring>
using namespace std;
int n;
const int maxn=10100;
int ans[maxn];
int a[maxn],b[maxn];
char s1[maxn],s2[maxn];
int lena,lenb;
void swap(int &a,int &b){
a=a^b;b=b^a;a=a^b;
}
int main(){
scanf("%s %s",s1,s2);
lena=strlen(s1),lenb=strlen(s2);
for(int i=0;i<lena;++i)
a[i]=s1[lena-i-1]-'0';
for(int i=0;i<lenb;++i)
b[i]=s2[lenb-i-1]-'0';
int len=lena>lenb?lena:lenb;
bool flag=0;
for(int i=len-1;i>=0;--i){//比较两数大小,通过比较两数最高的相等的位数,
if(a[i]>b[i]) break;
if(a[i]<b[i]){
flag=1;break;
}if(i==0){
printf("0");return 0;//说明两数想等
}
}
if(flag) printf("-");//b数较大所以a-b为负
if(flag) for(int i=0;i<len;++i) swap(a[i],b[i]);//b数较大,所以交换两值
for(int i=0;i<len;++i){
ans[i]=a[i]-b[i];
if(ans[i]<0) a[i+1]--,ans[i]+=10;
}
while(ans[len]==0) --len;
while(len>=0) printf("%d",ans[len]),--len;
}
减法高精-低精与加法同理
高精度乘法
高精乘高精一定要知道一件事
从数组第0位(作为个位数)开始,a数的第i位和第j位相乘为积的第i+j为数
可以自己用竖式模拟一下
高精*高精
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn=2e4+10;
char s[maxn];
int a[maxn],b[maxn];
int ans[maxn];
int main(){
scanf("%s",s);
int lena=strlen(s);
for(int i=0;i<lena;++i) a[i]=s[lena-i-1]-'0';
scanf("%s",s);int lenb=strlen(s);
for(int i=0;i<lenb;++i) b[i]=s[lenb-i-1]-'0';
for(int i=0;i<lena;++i)
for(int j=0;j<lenb;++j){
ans[i+j]+=a[i]*b[j];
ans[i+j+1]+=ans[i+j]/10;
ans[i+j]%=10;
}
int len=lena+lenb;
while(ans[len]==0 && len>=0) --len;
if(len==-1) printf("0");
else while(len>=0) printf("%d",ans[len]),--len;
}
高精*低精
同理(雾
高精度除法
高精÷高精
(容我鸽一鸽)(逃
高精÷低精
高精除低精
高精逐渐从高位转化为长整形,再除以低精
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int maxn=5e4+10;
char a[maxn];//a为高精度数
long long b,len;bool flag=0;//b为低精度数,flag表示是否输出过商
int main(){
cin>>a>>b;len=strlen(a);long long n=0,f;//n为被除数,f为余数
for(int i=0;i<len;++i){
n=n*10+a[i]-48;
f=n/b;
n%=b;
if(flag || f) flag=1,cout<<f;
}return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号