LiMaosen-2022-SkeletonPartedGraphScattering-ECCV

Skeleton-Parted Graph Scattering Networks for 3D Human Motion Prediction #paper

1. paper-info

1.1 Metadata

  • Author:: [[Maosen Li]], [[Siheng Chen]], [[Zijing Zhang]], [[Lingxi Xie]], [[Qi Tian]], [[Ya Zhang]]
  • 作者机构:: 南京大学
  • Keywords:: #GCN , #DCT
  • Journal:: #ECCV
  • Date:: [[2022-07-31]]
  • 状态:: #Done
  • 链接:: http://arxiv.org/abs/2208.00368
  • 阅读时间:: 2023.01.04

1.2.Abstract

Graph convolutional network based methods that model the body-joints' relations, have recently shown great promise in 3D skeleton-based human motion prediction. However, these methods have two critical issues: first, deep graph convolutions filter features within only limited graph spectrums, losing sufficient information in the full band; second, using a single graph to model the whole body underestimates the diverse patterns on various body-parts. To address the first issue, we propose adaptive graph scattering, which leverages multiple trainable band-pass graph filters to decompose pose features into richer graph spectrum bands. To address the second issue, body-parts are modeled separately to learn diverse dynamics, which enables finer feature extraction along the spatial dimensions. Integrating the above two designs, we propose a novel skeleton-parted graph scattering network (SPGSN). The cores of the model are cascaded multi-part graph scattering blocks (MPGSBs), building adaptive graph scattering on diverse body-parts, as well as fusing the decomposed features based on the inferred spectrum importance and body-part interactions. Extensive experiments have shown that SPGSN outperforms state-of-the-art methods by remarkable margins of 13.8%, 9.3% and 2.7% in terms of 3D mean per joint position error (MPJPE) on Human3.6M, CMU Mocap and 3DPW datasets, respectively.

关键词：GCN,HMP,DCT

2. Introduction

  • 领域:: 3D skeleton-based human motion prediction
  • 之前的方法::
    1. state model to capture the shallow dynamics
    2. deep learning area:
      1. RNN-based
      2. GCN-based
  • 作者主要是针对GCN-based方法。
    • 问题::
      1. 给定图结构后，标准的图卷积只能在有限的的图谱内过滤特征，而不能显著得保留更丰富的波段。(感觉类似于生成模型的模式坍塌问题，只能集中于主要的特征，而忽略了其他边缘特征。)
      2. 现存的方法都用单一的图去对整个身体结构进行建模，不能够学习到身体结构之间的多模态。(就是将身体拆分，分开学习，学习到更多的模式。)
    • 解决办法::
      1. 提出了一种自适应图散射技术(adaptive graph scattering technique):: 一种树形结构的波段图过滤器，能够将特征解构到多种图波段。主要包括三种技术(1. 基于数学的特殊波段过滤；2. 自适应过滤参数； 3.特征过滤层 )
      2. 将人体结构分层。
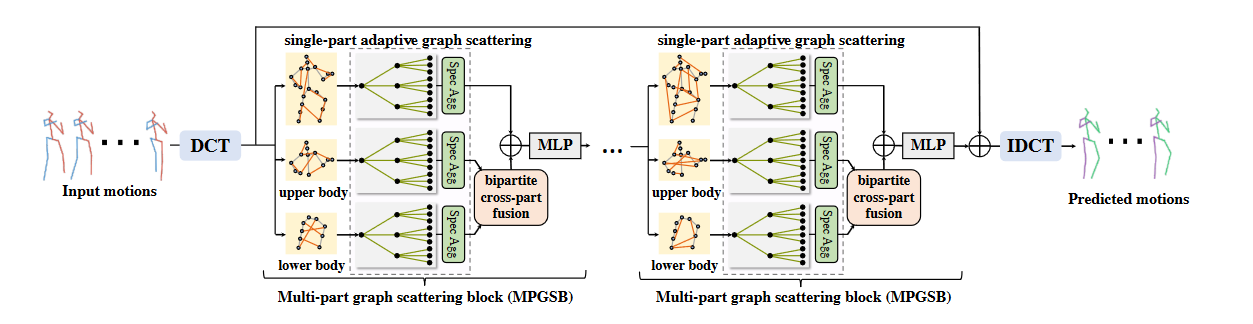
    • 模型主要结构，如Fig1
      1. skeleton-parted graph scattering network(SPGSN):: 将人体结构分层，进行特征波段筛选。
      2. multi-part graph scattering block(MPGSB):: 进行波段过滤。由二部分构成，
        1. single-part adaptive graph scattering:: 用MPGSB去概括部分身体部分的特征。
        2. bipartite cross-part fusion:: 用于概括不同身体部分的特征。

Fig.1. SPGSN的结构，首先利用DCT将时间序列信息转为频率信息，然后通过MPGSBs对身体的不同部分进行特征筛选，然后通过二分交叉融合(bipartite cross-part fusion)进行特征概括，最后通过IDCT将频率信息转为时间序列信息。

Source: 源paper

3. Skeleton-Part Graph Scattering Network

符号描述::
\(X^{(t)}\in \mathbb{R}^{M\times 3}\):: t时刻的动作。
\(\mathbb{X} = [X_{(1)},...,X^{(T)}]\):: 动作序列
\(\mathbb{X}^-\)::历史序列
\(\mathbb{X}^+\)::预测序列

3.1 模型结构

模型如Fig.1
输入历史序列\(\mathbb{X}^-\in\mathbb{R}^{T\times M \times 3}\)，首先将\(\mathbb{X}\)reshape成\(\mathcal{X}^-\in\mathbb{R}^{T\times 3M}\)，目的是将每个时间戳的所有关节坐标独立地作为空间域的独立单位；然后通过DCT,\(X^{-}= DCT(\mathcal{X}^-)\in\mathbb{R}^{M' \times 3}\)其中\(M' = 3M\) ，然后通过多个multi-part graph scattering blocks(MPGSBs)，同时这里使用了类似残差连接的方式，目的是让SPGSN捕获特征位移以进行稳定预测；最后通过IDCT转换为时间序列信息。

4.multi-part graph scattering blocks(MPGSB)

每个MPGSB块由两部分构成::

  1. single-part adaptive graph scattering:: 特征提取，学习身体部位的大波段信息。
  2. bipartite cross-part fusion:: 特征融合

4.1 single-part adaptive graph scattering

该部分由两部分构成::

  1. adaptive graph scattering decomposition
  2. adaptive graph spectrum aggregation
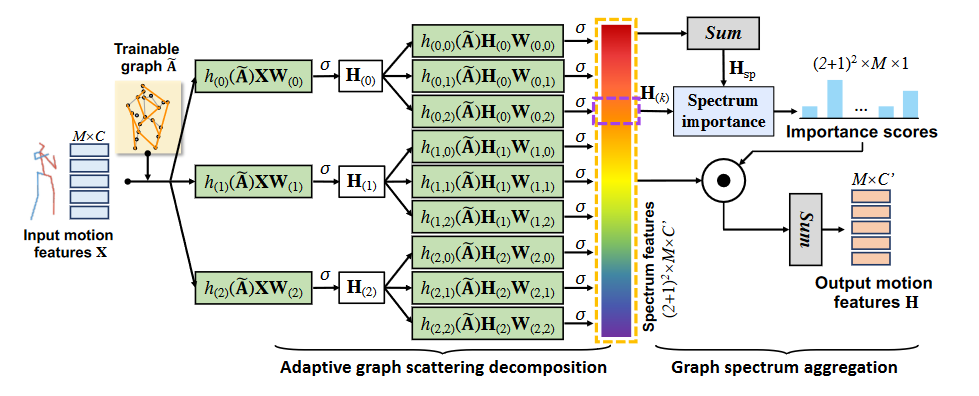
    adaptive graph scattering decomposition
    一个树形结构的网络，\(L\)层，树的结点层指数增长。以一层说明::
    输入DCT-formed pose feature\(X\in\mathbb{R}^{M'\times C}\) 和 对应的领接矩阵\(A\in\mathbb{R}^{M'\times M'}\)，然后通过一系列的带通图形滤波器(bandpass graph filters)\(\{ h_{(k)}(\tilde{A} )| k=0,1,...,K \}\) ,其中 \(\tilde{A}=\tilde{A} = 1/2(I+A/\left \| A \right \|_F^2 )\)，归一化；通过这些filter bank，得到特征::

\[H_{(k)}=\sigma (h_{(k)}XW_{(k)}) \]

其中\(W_{(k)}\)是可学习的参数，\(\sigma(.)\)用于分散图形频率表示，也就是激活函数。

为了能够让filter作用不同的图波段，通过数学先验对他进行初始化，然后通过可学习的系数对filter进行微调，计算方式如下::

\[\begin{array}{ll} h_{(k)}(\widetilde{\mathbf{A}})=\alpha_{(0,0)} \widetilde{\mathbf{A}}, & k=0 \\ h_{(k)}(\widetilde{\mathbf{A}})=\alpha_{(1,0)} \mathbf{I}+\alpha_{(1,1)} \widetilde{\mathbf{A}}, & k=1 \\ h_{(k)}(\widetilde{\mathbf{A}})=\sum_{j=1}^{k} \alpha_{(k, j)} \widetilde{\mathbf{A}}^{2^{j-1}}, & k=2, \ldots, K, \end{array} \]

其中\(\alpha_{(k,j)}\)为可学习的系数。当\(k=0\)时，\(\alpha_{(0,0)}=1\)，当\(k>0\)时，\(\alpha_{(k,k-1)=1}, \ \alpha_{(k,k)}=-1\)，其他的\(\alpha_{(k,j)}=0\)。

重复上面的过程，每一层都得到\(K+1\)个分支，最后经过\(L\)层后，就会得到\((K+1)^L\)个channels，对应不同的波段。
adaptive graph spectrum aggregation
对不同波段的信息进行筛选融合，也就是特征筛选，通过对不同的波段特征加入可学习的参数，计算方式如下::

\[\mathbf{H}=\sum_{k=0}^{(K+1)^{L}} \omega_{k} \mathbf{H}_{(k)} \in \mathbb{R}^{M^{\prime} \times C^{\prime}} \]

\(\mathcal{w}_k\)就是频谱重要性分数系数，计算方式如下::

\[\omega_{k}=\frac{\exp \left(f_{2}\left(\tanh \left(f_{1}\left(\left[\mathbf{H}_{\mathrm{sp}}, \mathbf{H}_{(k)}\right]\right)\right)\right)\right)}{\sum_{j=0}^{(K+1)^{L}} \exp \left(f_{2}\left(\tanh \left(f_{1}\left(\left[\mathbf{H}_{\mathrm{sp}}, \mathbf{H}_{(j)}\right]\right)\right)\right)\right)} \]

其中\(f_1(.) \ and \ f_2(.)\)为全连接层，\([.,.]\)为沿着特征维度串联，\(H_{sp}\in\mathbb{R}^{M'\times C'}\)的计算方式::

\[\mathbf{H}_{\mathrm{sp}}=\operatorname{ReLU}\left(\frac{1}{(K+1)^{L}} \sum_{k=0}^{(K+1)^{L}} \mathbf{H}_{(k)} \mathbf{W}_{\mathrm{sp}}\right) \]

例子
\(L=2 \ K=2\)


Fig. 2. single-part adaptive graph scattering结构例子，K=2,L=2

Source: 源paper

4.2 Bipartite Cross-Part Fusion

对不同身体部分的特征进行选择融合。在本paper中，作者将人体结构分为上下两部分。
输入\(H_{\uparrow}\in\mathbb{R}^{M_\uparrow \times C'}\)上半部分的特征，\(H_{\downarrow }\in\mathbb{R}^{M_\downarrow \times C'}\)下班部分特征，首先得到upper-to-lower affinity matrix::

\[\mathbf{A}_{\uparrow 2 \downarrow}=\operatorname{softmax}\left(f_{\uparrow}\left(\mathbf{H}_{\uparrow}\right) f_{\downarrow}\left(\mathbf{H}_{\downarrow}\right)^{\top}\right) \in[0,1]^{M_{\uparrow} \times M_{\downarrow}}, \]

\(f_{\uparrow}(.) \ and \ f_{\downarrow}(.)\)为两个编码网络。
得到映射矩阵后，更新两部分的特征通过下面的公式::

\[H'_{\downarrow} = H_{\downarrow} + \mathbf{A}_{\uparrow 2 \downarrow}^TH_{\uparrow} \]

最后，将整个身体的特征于部分混合特征融合，通过下面的公式得到\(H'\in\mathbb{R}^{M'\times C'}\)

\[H'=MLP(H+(H'_{\uparrow}\oplus H'_{\downarrow})) \]

\(\oplus: \mathbb{R}^{M_{\uparrow} \times C^{\prime}} \times \mathbb{R}^{M_{\downarrow} \times C^{\prime}} \rightarrow \mathbb{R}^{M^{\prime} \times C^{\prime}}\)放置来自不同身体部位的关节以与原始身体对齐。

4.3 Loss function

重构损失::

\[\mathcal{L}=\frac{1}{N} \sum_{n=1}^{N}\left\|\mathbb{X}_{n}^{+}-\widehat{\mathbb{X}}_{n}^{+}\right\|^{2} \]

5. Experiments

  • dataset
    • Human 3.6M
    • CMU Mocap
    • 3D pose in the wild(3DPW)

6. 代码


Fig.3.SPGSN model 逻辑

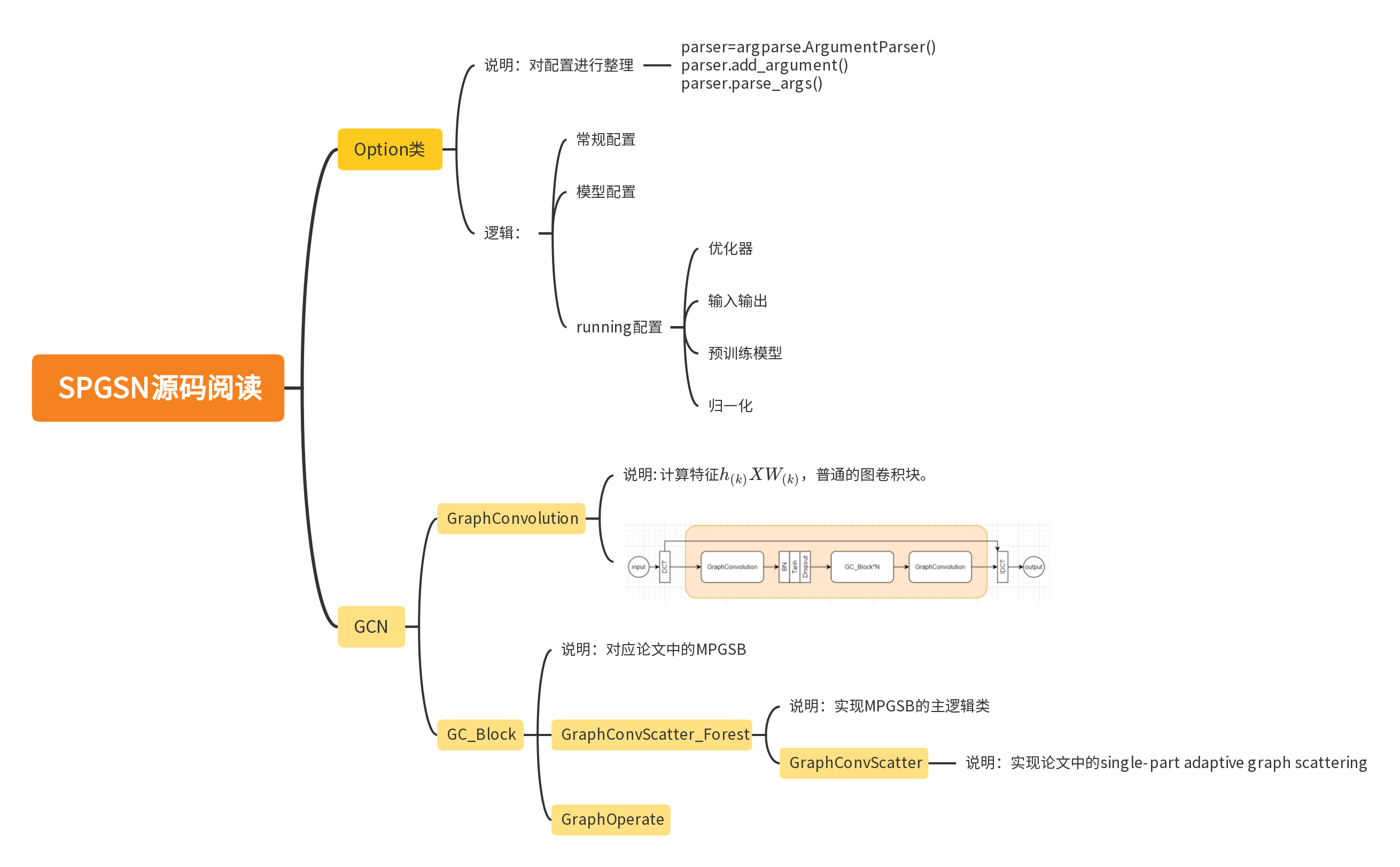
DCT 实现

def get_dct_matrix(N):
    dct_m = np.eye(N)
    for k in np.arange(N):
        for i in np.arange(N):
            w = np.sqrt(2 / N)
            if k == 0:
                w = np.sqrt(1 / N)
            dct_m[k, i] = w * np.cos(np.pi * (i + 1 / 2) * k / N)
    idct_m = np.linalg.inv(dct_m)
    return dct_m, idct_m
   

7. 总结

总得来说就是针对模型学习会集中到低频率的特征，而忽略高频段的特征，于是将特征解构。

posted @ 2023-01-06 12:38  GuiXu40  阅读(62)  评论(0)  编辑  收藏  举报