Mohamed Elfeki-2019-GDPP Learning Diverse Generations Using Determinantal Point Process

GDPP: Learning Diverse Generations Using Determinantal Point Process #paper

---

1. paper-info

1.1 Metadata

• Author:: [[Mohamed Elfeki]], [[Camille Couprie]], [[Morgane Riviere]], [[Mohamed Elhoseiny]]
• 作者机构::
• Keywords:: #DPP
• Journal:: #ICML, #PMLR
• Date:: [[2019-11-24]]
• 状态:: #Done
• 链接:: http://proceedings.mlr.press/v97/elfeki19a.html
• 修改时间:: 2022.12.27

1.2. Abstract

Generative models have proven to be an outstanding tool for representing high-dimensional probability distributions and generating realistic-looking images. An essential characteristic of generative models is their ability to produce multi-modal outputs. However, while training, they are often susceptible to mode collapse, that is models are limited in mapping input noise to only a few modes of the true data distribution. In this work, we draw inspiration from Determinantal Point Process (DPP) to propose an unsupervised penalty loss that alleviates mode collapse while producing higher quality samples. DPP is an elegant probabilistic measure used to model negative correlations within a subset and hence quantify its diversity. We use DPP kernel to model the diversity in real data as well as in synthetic data. Then, we devise an objective term that encourages generators to synthesize data with similar diversity to real data. In contrast to previous state-of-the-art generative models that tend to use additional trainable parameters or complex training paradigms, our method does not change the original training scheme. Embedded in an adversarial training and variational autoencoder, our Generative DPP approach shows a consistent resistance to mode-collapse on a wide variety of synthetic data and natural image datasets including MNIST, CIFAR10, and CelebA, while outperforming state-of-the-art methods for data-efficiency, generation quality, and convergence-time whereas being 5.8x faster than its closest competitor.

---

2. Introduction

• 领域：深度生成模型(GAN、VAE)
• 问题：模式坍塌，生成模型学习到真实数据的主流模式，而忽略了数据的边缘模式。
• 解决方法：利用Determinantal Point Processes (DPP)的特性，根据DPP的核，设计了一种基于DPP的损失函数，可以促进模型学习数据的多模态。
  注： 解决模型的模式坍塌问题的两种思路，1. 修改模型的训练过程以求达到更好的收敛过程。2.明确强制模型捕获不同的模式或映射回真实的数据分布。(添加损失函数) 3.在原有预训练好的生成模型的基础之上，重新映射潜在变量(DLow)

---

3. DPP

参考地址：

徐亦达教授 https://www.bilibili.com/video/BV14q4y1F752/?spm_id_from=333.999.0.0
课件地址：https://github.com/roboticcam/machine-learning-notes

DPP 是一个概率模型。

• 幂集 power set
  假设有集合\(\mathcal{Y}\)，那么幂集\(2^{\mathcal{Y}}\)就是\(\mathcal{Y}\)的所有子集(包括空集和全集)所组成的集合。假设\(\mathcal{Y}=\{1, 2\}\)，那么

\[2^\mathcal{Y} = \Big\{ \emptyset, \{1\}, \{1, 2\}, \{2\} \Big\}。 \]

行列式点过程\(\mathcal{P}\)是在\(ground \ set \ \mathcal{Y}\)的幂集\(2^\mathcal{Y}\)上的概率密度。通过\(\mathcal{P}\)采样得到的子集可以是空集，也可以是全集\(\mathcal{Y}\)。假设\(Y\)是由\(\mathcal{P}\)从\(2^\mathcal{Y}\)中随机采样得到的一个子集，对于任意的\(A \subset \mathcal{Y}\)，有

\[p(A \subset {Y}) = det(K_{A)}\tag{1} \]

公式\(\color{blue}{(1)}\)中的变量的含义分别是：

• \(Y\)是由行列式点过程\(\mathcal{P}\)随机采样得到的一个随机子集。
• \(A \in \mathcal{Y}\)是\(\mathcal{Y}\)的任意子集
• \(p(A \subset {Y})\)表示\(A\)中所有元素在采样中被命中的概率。(A = \(\emptyset\), 则\(p(A \subset {Y})=1\) )
• \(K\)是DPP kernel

3.1 DPP kernel

矩阵\(K\)被称作DPP kernel，是一个\(N\times N\)的实对称方阵。\(K\)的元素\(K_{ij}\)可以理解为集合\(\mathcal{Y}\)中第\(i,j\)个元素之间的相似度 ，\(K_A\)是根据\(A\)中元素从\(K\)中按行按列索引得到的方阵，也即\(K_A\)是\(K\)的主子式。\(det(K_A)\)是矩阵\(K_A\)的行列式值。

由于\(\forall A, p(A \subset Y) \ge 0\)，所以\(K\)是半正定矩阵(主子式大于等于零的矩阵是半正定矩阵。) 同时由于\(p(A \subset Y) \le 1\)，\(K\)的特征值都小于1。我们甚至与可以放松\(p(A \subset Y) \le 1\)条件，这样\(p(A \subset Y)\)只需要正比于\(det(K_A)\)即可：

\[\begin{equation} p(A \subset Y) \propto \det(K_A)。 \end{equation} \tag{2}\]

\(K_{ij}\)越大的样本，被采样出来的概率越大

当\(A={i}\)时，\(p(\{i\} \subset Y) = K_{ii}\)表示元素\(i\)被采样出来的概率。实际上\(p(\{i\} \subset Y)\)是个边缘概率。因为\(p(\{i\} \subset Y) = \sum_{x \subset 2^{\mathcal{Y}}} p(\{i\} \cup x \subset Y)\)
\(K_{ij}\)越大的两个样本\({i,j}\)越相似，被同时采样出来的概率越低
假设\(A={i,j}\)， 那么

\[\begin{equation} \begin{split} p(\{i,j\} \subset Y) &= \det(\begin{bmatrix} K_{ii} & K_{ij} \\\ K_{ji} & K_{jj} \end{bmatrix}) \\ &= K_{ii}\cdot K_{jj} - K_{ij} - K_{ji} \\ &= K_{ii}\cdot K_{jj} - 2K_{ij} \\ &= K_{ii}\cdot K_{jj} - 2K_{ji}。 \end{split} \end{equation} \tag{3}\]

由公式(3)可以很容易得到：当元素\(i,j\)相似度很高的时候，\(i,j\)被同时采样的概率就很小。
注：难点在于DPP kernel的定义方式。任意点\(i\)被采样出来的概率应该一样；越相似的点越不容易被同时采样出来。

3.2 L-Ensembles

由于DPP kernel没有定义确定子集被采样到的概率，于是定义如下：

\[Pr_L(\mathbb{Y}=Y)\propto det(L_Y) \]

\(L\)必须是半正定矩阵
Geometry interpretation
可用\(Gram \ matrix\)作为矩阵\(L\)

\[\begin{array}{l} X=\left[\begin{array}{llll} x_{1} & x_{2} & \ldots & x_{n} \end{array}\right] \Longrightarrow \\ L\left(x_{1}, \ldots, x_{n}\right)=X^{\top} X=\left(\begin{array}{cccc} \left\langle x_{1}, x_{1}\right\rangle & \left\langle x_{1}, x_{2}\right\rangle & \ldots & \left\langle x_{1}, x_{n}\right\rangle \\ \left\langle x_{2}, x_{1}\right\rangle & \left\langle x_{2}, x_{2}\right\rangle & \ldots & \left\langle x_{2}, x_{n}\right\rangle \\ \vdots & \vdots & \ddots & \vdots \\ \left\langle x_{n}, x_{1}\right\rangle & \left\langle x_{n}, x_{2}\right\rangle & \ldots & \left\langle x_{n}, x_{n}\right\rangle \end{array}\right) \\ \end{array} \]

几何意义：以\(x_1,x_2,...,x_n\)为边的超多边体的体积。
L-Ensembles中的归一化
Theorem 1

\[\sum_{A\subseteq Y \subseteq \Omega }^{} det(L_Y) = det(L+I_{\bar{A} }) \]

当\(A = \emptyset\)时，

\[\begin{aligned} \sum_{\emptyset \subseteq Y \subseteq \Omega} \operatorname{det}\left(L_{Y}\right) & =\sum_{Y \subseteq \Omega} \operatorname{det}\left(L_{Y}\right) \\ & =\operatorname{det}\left(L+\mathbf{I}_{\bar{\emptyset}}\right) \\ & =\operatorname{det}\left(L+\mathbf{I}_{\Omega}\right) \\ & =\operatorname{det}(L+\mathbf{I}) \end{aligned} \]

DPP kernel 与 L-Ensembles的相互转化
详细推导过程请看徐教授的课件

\[K = L(L+I)^{-1} = I-(L+I)^-1 \]

\[L=\sum_{n=1}^{N} \lambda_{n} v_{n} v_{n}^{\top} \Longrightarrow K=\sum_{n=1}^{N} \frac{\lambda_{n}}{\lambda_{n}+1} v_{n} v_{n}^{\top} \]

其中，\(\lambda_{n}\)为\(L\)的特征值，\(v_{n}\)为特征值对应的特征向量。
Quality and Diversity

Fig. 推导过程

根据上面的推导过程，可以将\(q_i\)看做每一个item的质量分数(quality score)

3.3 Sampling DPP

https://blog.csdn.net/qq_23947237/article/details/90698325

Fig. 采样算法

4. Generative Determinantal Point Processes

关键点

• 多样性
• 精确性

Fig.1. GDPP说明

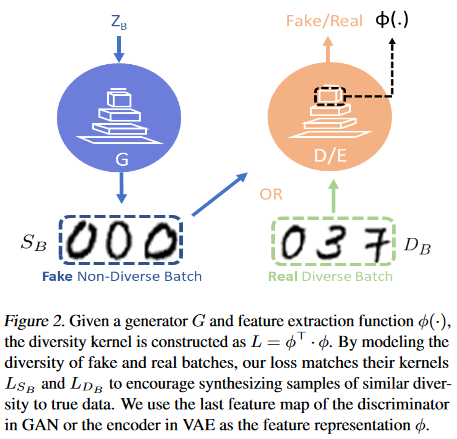
如Fig1.所示，我们希望真实图片\(D_B\)，生成的图片\(S_B\)是由同一个DPP kernel采样得到的：$$\begin{equation}
p(S_B \subset Y) \propto \det(L_{D_B})。
\end{equation} \tag{4}$$

4.1 计算DPP kernel \(L_{s_b}，L_{D_b}\)

\(L_{S_{B}(i,}j)\)表示这个batch中第\(i,j\)两个元素的相似度，值越大越相似。这样可以通过一个特征提取函数\(\phi(I)\) ，对任意一个图片\(I\)，都能够提取一个图像特征\(\phi(I)\)。
然后图片之间的相似度可以通过特征内积来计算：

\[L_{D_B} = \phi(D_B)^T\phi(D_B) \]

\[L_{S_B} = \phi(S_B)^T\phi(S_B) \]

为了不引入额外的参数，文章中直接用判别器D作为\(\phi(.)\)。取判别器倒数第二个全连接层的输出作为样本特征(如Fig1所示)。

4.2 损失函数

最直接的想法：

\[\mathcal{L}^{DPP}=L_{S_B}-L_{D_B} \]

文献[1]中指出这是一个非限制性的优化问题。让\(L_{S_B},L_{D_B}\)的特征值与特征向量互相匹配是另一种解决方案：

\[\begin{equation} \begin{split} \mathcal{L}^{DPP} &= \mathcal{L}_M + \mathcal{L}_s \\ &= \sum_i ||\lambda_{real}^i - \lambda_{fake}^i|| \\ &- \sum_i \hat{\lambda}_{real}^i \cos(v_{real}^i, v_{fake}^i) \end{split} \end{equation} \tag{5} \]

其中\(\lambda_{fake}^{i}, \lambda_{real}^i\)分别是\(L_{S_B},L_{D_B}\)的第\(i\)个特征值，\(v_{real}^i, v_{fake}^i\)为特征向量。
所以最后的损失函数为

\[\begin{equation} \mathcal{L}^{DPP-GAN/VAE} = \mathcal{L}^{GAN/VAE} + \mathcal{L}^{DPP} \end{equation}\]

参考文献

[1]Li F, Fu Y, Dai Y H, et al. Kernel learning by unconstrained optimization[C]//Artificial Intelligence and Statistics. PMLR, 2009: 328-335.
[2]Determinantal point process 入门 https://blog.csdn.net/qq_23947237/article/details/90698325
[3]DPPy: Sampling Determinantal Point Processes with Python https://github.com/guilgautier/DPPy
[4]# Determinental point processes https://andrewcharlesjones.github.io/journal/dpps.html